ДАВЛЕНИЕ - это среднее значение нормальных напряжений.

Напряжения, которые распространяются параллельно поверхности, называются СДВИГОВЫМИ.

Напряжения, которые передаются перпендикулярно к поверхности, называются НОРМАЛЬНЫМИ.

Напряжение, действующее в упругой твёрдой среде, приводит к деформации среды. Простейшим примером деформации является СОКРАЩЕНИЕ ОБЪЁМА, происходящее благодаря СЖИМАЕМОСТИ СРЕДЫ под действием приложенного ДАВЛЕНИЯ.

НОРМАЛЬНАЯ ДЕФОРМАЦИЯ определяется как приращение длины твёрдого тела к исходной длине.

СДВИГОВАЯ ДЕФОРМАЦИЯ определяется как ПОЛОВИНА УМЕНЬШЕНИЯ ПРЯМОГО УГЛА, выделенного в среде при деформации. В результате тектонических процессов поверхность Земли непрерывно деформируется.

 

МАССОВЫЕ (ОБЪЁМНЫЕ) И ПОВЕРХНОСТНЫЕ СИЛЫ

 

Имеется два типа сил, действующих на элемент твёрдой среды: массовые (объёмные) и поверхностные.

Массовые силы действуют в каждой точке объёма среды.

Величина массовой силы, действующей на элемент среды, пропорциональна его объёму или массе. Например, сила тяжести - вес элемента среды, равный произведению массы на ускорение силы тяжести g. Если ввести плотность среды r, равную массе единицы объёма, то действующую на элемент силу тяжести можно записать как произведение величины rg на объём элемента.

Таким образом, сила тяжести, действующая на единицу массы, есть g, а сила тяжести, действующая на единицу объёма - rg.

Плотность, вообще говоря, зависит от давления. При высоких давлениях, господствующих на больших глубинах в мантии, увеличение плотности пород может составить до 50% значения плотности при нулевом давлении.

Мантийная порода	Плотность мантийной породы, кг/м3
Типичная
Базальт и габбро
Гранит и диорит	2650 - 2800

В отличие от массовых сил, поверхностные силы приложены ТОЛЬКО К ПОВЕРХНОСТИ, ограничивающей элемент объёма. Они обусловлены межатомными силами, действующими со стороны материала, находящегося с одной стороны от поверхности, на материал, находящийся с противоположной стороны.

Величина поверхностной силы прямо пропорциональна площади поверхности, на которую она действует. Кроме того, эта сила зависит от ориентации поверхности.

ПРИМЕР: Рассмотрим силу, приложенную к основанию столба породы на глубине у от поверхности Земли и уравновешивающую вес столба. (Рис. 2.1. Массовая и поверхностная силы, действующие на вертикальный столб породы).

Площадь поперечного сечения равна dA;

Вес столба с площадью поперечного сечения dA равен rgydA;

Поверхностная сила, уравновешивающая этот столб, s_ууdА направлена вверх и распределена по горизонтальной поверхности площадью dA на глубине у.

ДОПУЩЕНИЯ: на боковые поверхности не действует никаких вертикальных сил и плотность r постоянна.

ТАКИМ ОБРАЗОМ: s_уу есть сила, приходящаяся на единицу площади и направленная перпендикулярно горизонтальной поверхности, Т,Е, НАПРЯЖЕНИЕ.

Поскольку силы, действующие на равновесный столб породы, должны быть равны, получаем, что

s_уу = rgy. (1)

Сила, приходящаяся на единичную площадь и перпендикулярная горизонтальным плоскостям, линейно растёт с глубиной.

Нормальное напряжение, вызванное весом вышележащих пород, называется ЛИТОСТАТИЧЕСКИМ НАПРЯЖЕНИЕМ или ДАВЛЕНИЕМ.

НАПРИМЕР, литостатическое напряжение в основании континентальной коры при её средней плотности 2750 кг/м³ и толщине коры 35 км (3.5 ×10⁴ м) будет равно:

s_уу = 2750 кг/м³×10 м/с²×3.5×10⁴м = 9.625 ×10⁸Па = 962.5 МПа (9.625 кбар).

В системе СИ единицей давления или напряжения является паскаль (Па); 1 Па = 1 кг×/м×с²;. 1 мегапаскаль МПа = 10⁶ Па; 1 бар = 10⁵ Па = 0.98692 атм.

Поскольку плотность жидкой мантии (3300 кг/м³ ) больше плотности пород континента (2750 кг/м³), то можно считать, что континент является блоком, плавающим в мантии (Рис.2.2. Континентальный блок, "плавающий" на "жидкой" мантии.) Согласно закону Архимеда, выталкивающая сила, действующая на континент, равна весу вытесненной мантийной породы. В основании континента напряжение s_уу = r_кgh, где r_к - плотность континентальных пород, h - толщина континента. На этой же глубине в мантии напряжение составит s_уу = r_мgb, где r_м - плотность мантии, b - глубина погружения континента в мантию.

С другой стороны, согласно гидростатическому равновесию эти два напряжения должны быть равны:

r_кgh = r_мgb,т.е.r_кh = r_мb. (2)

Применительно к континентальной коре принцип гидростатического равновесия называется ПРИНЦИПОМ ИЗОСТАЗИИ.

Откуда можно определить:

1. Возвышение континента над окружающей мантией: h - b = h - r_к/r_мh = h (1-r_к/r_м); (3)

2. Глубину океанического бассейна относительно поверхности континента (Рис.2.3. Структура континентального и океанического регионов):

(4)

где:

Ø h_кк, r_кк - толщина и плотность континентальной коры;

Ø h_в - глубина океана;

Ø r_в - плотность воды;

Ø h_ок - толщина океанической коры;

Ø r_ок - плотность океанической коры;

Ø r_м - плотность мантии.

 

ЭЛЕМЕНТЫ ТЕОРИИ ДЕФОРМАЦИЙ

Деформация (изменение расстояния) между отдельными точками среды - характерная черта движения СС.

Удлинение или укорочение произвольно направленного единичного отрезка , проходящего через точку среды М(х₁,х₂,х₃), вычисляется по формуле

(1.19)

где a_i = Cos (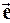, ) - направляющие косинусы отрезка; e_ii - удлинения (укорочения) единичных отрезков, направленных параллельно координатным осям Ох_i ; e_ij = e_ji (i ¹ j) -изменения первоначально прямых углов, образованных отрезками, направленными параллельно координатным осям Ох_i , Оx_j.

Таким образом, деформация элементарного объёма среды в окрестности точки М полностью определяется шестью величинами e_ij , которые называются КОМПОНЕНТАМИ СИММЕТРИЧНОГО ТЕНЗОРА ДЕФОРМАЦИЙ.

Для малых деформаций (<< 1) верны следующие соотношения Коши(в декартовой системе координат):

(i, j = 1,2,3), (1.20)

где u _i- компоненты вектора перемещения в точке М.

Тройка перпендикулярных направлений, где в окрестности точки деформация элемента определяется без изменения прямых углов (e_ij = 0, i ¹ j), только удлинением или укорочением e_ij = e_i , называется ГЛАВНЫМИ ОСЯМИ ДЕФОРМАЦИЙ, а величины e_i (i - 1,2,3) - ГЛАВНЫМИ УДЛИНЕНИЯМИ, которые могут быть найдены из следующего соотношения

,

где - символ Кронекера

Коэффициенты этого уравнения не зависят от выбора системы координат, они инвариантны.

Первый коэффициент этого уравнения имеет очень простой геометрический смысл: это относительное изменение объёма в окрестности точки.

. (1.21)

Коэффициенты a и b геометрического смысла не имеют и поэтому не являются характеристикой деформаций.

Характеристикой искажения формы элемента сплошной среды служит инвариантная величина

,

ИНТЕНСИВНОСТЬ ДЕФОРМАЦИЙ СДВИГА

 

Величины g₁ = e₂ - e₃ , g₂ = e₃ - e₁ , g₃ = e₁ - e₂ - называютсяГЛАВНЫМИ СДВИГАМИ

G » 1.08 g_max

где g_max - наибольший из главных сдвигов.

В произвольной декартовой системе координат величина Г вычисляется по формуле

.(1.22)

Иногда используется величина, которая называется интенсивностью деформации, или приведённой деформацией

.

Для характеристики деформационного состояния служит параметр Надаи

(1.23)

который изменяется от - 1 (при чистом удлинении) до + 1(при чистом укорочении). В случае чистого сдвига он равен 0. При всестороннем расширении или сжатии параметр m_e не имеет смысла.

Часто компоненты деформации представляют в следующем виде:

(1.24)

где e_ij - компоненты, характеризующие только деформации сдвига, называются компонентами девиатора деформаций; d_ij - символ Кронекера.

Отсюда следует, что компоненты тензора деформации растяжения (сжатия) e_ii отличаются от соответствующих компонент девиатора e_ii на 1/3 объёмной деформации, а компоненты деформации сдвига не отличаются, т.е.

Если известны компоненты деформации e_ij как функции декартовых координат x_i, то для однозначного определения трёх компонент u_i вектора перемещений из шести соотношений (1.20) НЕОБХОДИМО И ДОСТАТОЧНО, чтобы функции e_ij удовлетворяли условиям совместимости (ИЛИ НЕРАЗРЫВНОСТИ) деформаций Сен-Венана:

(1.25)

и т.д., всего шесть условий (остальные получаются из выписанных круговой заменой индексов 1 ® 2 ® 3 ® 1).

Таким образом, условия совместимости (1.25) являются уравнениями, связывающими компоненты e_ij тензора деформаций.

Для анализа больших деформаций, если главные оси при деформации не поворачиваются, используются НАТУРАЛЬНЫЕ УДЛИНЕНИЯ (укорочения)

где l_i0, l_i - начальные и текущие длины элемента в соответствующих направлениях.

Характерные соотношения для малых деформаций являются справедливыми и для натуральных удлинений.

Если скорость частиц сплошной среды `v = (v₁, v₂, v₃), то за бесконечно малый промежуток времени dt среда испытывает бесконечно малую деформацию, определяемую перемещениями u_i = v_idt (i =1, 2, 3).

Компоненты этих деформаций, вычисленные по формулам (1.20), имеют общий множитель dt, разделив на который получаем

(1.26)

где x_ij - компоненты тензора скоростей деформаций.

Величины x_ij определяют скорости удлинения (укорочения) единичных отрезков в направлениях Ox_i, x_ij (i ¹ j) - угловые скорости изменения первоначально прямых углов, составленных единичными отрезками вдоль координатных осей.

Подобно формуле (1.19) скорость удлинения (укорочения) любого единичного отрезка вычисляется по формуле

Аналогично соотношениям (1.21) - (1.23) инвариантами скорости деформации являются:

ü скорость относительного объёмного расширения (сжатия)

x = x₁₁ + x₂₂ + x₃₃ = x₁ + x₂ + x₃ = div`v; (1.28)

ü интенсивность скоростей деформации сдвига относительно главных осей

(1.29)

где g₁ = x₂ - x₃, g₂ = x₃ - x₁, g₃ = x₁ + x₂- главные скорости сдвигов (относительно произвольной системы координат Н выражается формулой 1.22);

ü параметр Надаи w_x = 2g₁ / g₂ - 1.

Компоненты скоростей деформации x_ij , как и компоненты деформации e_ij не могут быть произвольными. Они должны удовлетворять условиям совместимости (аналогичным условиям 1.25).

Подобно (1.24) для компонент тензора {x_ij}скоростей деформаций верно соотношение

x_ij = l_ij + 1/3xd_ij, (1.30)

где l_ij - компоненты, характеризующие только скорости деформации сдвига, называемые компонентами девиатора скорости деформаций.

 

УПРУГОСТЬ И ИЗГИБ

 

Упругими деформацияминазываются такие, которые после снятия приложенных напряжений исчезают.

Материалы, в которых при данных напряжениях возникают упругие деформации, называются упругими материалами.

Почти все твёрдые тела (горные породы) при относительно низких температурах и давлениях и не слишком высоких напряжениях являются упругими.

Упругие деформации в твёрдых телах прямо пропорциональны приложенным напряжениям.

Изотропными материалами называются такие, у которых упругие свойства не зависят от направления.

При высоких уровнях напряжений и температур в породах проявляются отклонения от упругого поведения.

При низких температурах и всесторонних давлениях породы проявляют хрупкие свойства и при значительных девиаторных напряжениях разрушаются.

В недрах Земли, где всестороннее давление растёт с глубиной и когда оно достигает предела хрупкого разрушения, в породе возникают пластические деформации.

Пластическими называют непрерывные, необратимые деформации, происходящие без разрушения.

При этом, после того, как действие силы, вызывающей пластическую деформацию прекращается, деформация частично сохраняется (не исчезает полностью).

СООТНОШЕНИЯ ЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИ

Упругая твёрдая среда называется линейной и изотропной в том случае, если напряжения в ней линейно связаны с деформациями, а механические свойства среды не зависят от направления.

В такой среде главные оси напряжений и деформаций совпадают. Связь между напряжениями и деформациямиудобно записать в системе координат, связанной с главными осями:

s₁=(l+2G)e₁ + l e₂+ le₃, (3.1)

s₂= le₁+ (l+2G )e₂ + le₃, (3.2)

s₃= le₁+ le₂ + (l+2G )e₃ (3.3)

где упругие модули l и G (модуль сдвига) называются параметрами Ламе.

Свойства среды таковы, что от действия компонент деформации e возникает напряжение (l+2G)e в том же направлении и напряжения le в других взаимно перпендикулярных направлениях:

(3.4)

(3.5)

(3.6)

где Е (модуль Юнга, меняется для горных пород в пределах 10 – 100 ГПа) и n (коэффициент Пуассона, меняется в пределах 0.1 – 0.4)- материальные параметры среды.

Главная компонента напряжения s создаёт деформацию s/E в направлении своего действия и деформации -ns/E в двух других взаимно перпендикулярных направлениях.

Упругие свойства среды характеризуют, задавая l и G или E и n. Эти параметры не являются независимыми.

Одноосное напряжённое состояние.В этом случае отлично от нуля только одно главное напряжение, например, s₁. s₂ = s₃ = 0 , тогда

(3.7)

Отсюда видно, что напряжение s₁ вызывает не только деформацию e₁ в направлении своего действия, но и деформации в перпендикулярных направлениях e₂ и e₃.

Если s₁ - напряжение сжатия, то e₁ - укорочение, а e₂ и e₃ - удлинения.

Эти деформации показаны на рис. 3.2, (Рис.3.2. Деформация под действием одноосного сжатия), где элементdxdydz стал короче в направлении оси n, но толще в направлении осей х и z.

В соответствии с равенствами (3.4)- (3.6) мы можем написать:

(3.8)

Сравнивая это равенство с (3.7), получаем:

(3.9)

Из (3.1) и (3.7) находим

, (3.10)

совместно с (3.8) для модуля Юнга получаем:

(3.11)

С помощью (3.9) (3.11) выражаем l и G через E и n:

(3.12)

(3.13)

В случае одноосного сжатия или растяжения соотношение (3.8) превращается в закон Гука:

s₁ = E e₁ (3.14)

Линейно-упругое тело называется иначе Гуковским телом.

Относительное изменение объёма (дилатация D) определяется в этом случае выражением:

D = e + e₂ + e₃ = e₁(1 - 2n) (3.15)

Из формулы видно, что уменьшение объёма, происходящее за счёт сокращения размера в направлении действия напряжения, компенсируется увеличением объёма за счёт расширения в перпендикулярных направлениях.

Из выражения (3.15) можно определить коэффициент Пуассона для несжимаемой среды, объём которой не меняется под действием приложенного напряжения.

Чтобы это реализовать, при одноосном сжатии n должно быть равно ½.Под действием одноосного сжатия несжимаемая среда сокращается в направлении приложенного напряжения и расширяется на величину, вдвое меньшую в каждом из перпендикулярных направлений.

Одноосная деформация.Состояние одноосной деформации характеризуется тем, что отличной от 0 является только одна главная компонента деформации,например, e₁.Тогда (3.1)- (3.3.) дают

s₁= (l + 2G)e₁ (3.19)

(3.20)

а (3.4)-(3.6) упрощаются следующим образом:

(3.21)

(3.22)

Плоское напряжённое состояние.Возникает тогда, когда имеется только одно нулевое главное напряжение, например, s₃ = 0,s₂ ¹ 0,s ₁¹ 0. (Рис.3.5. Плоское напряжённое состояние). Тонкая пластина нагружена с боков. Определим компоненты деформации (3.4) –(3.6)

(3.31)

(3.32)

(3.33)

Плоская деформация.В этом случае равна нулю только одна главная деформация , например, e₃ = 0. На рис. 3.7. (Пример плоской деформации) длинная балка жёстко зажата между двумя стенками, которые не позволяют ей расширяться или сжиматься в продольном направлении. Кроме того, вдоль всей длины на балку действуют равномерно распределённые напряжения s₁и s_2.

(3.1) - (3.3) в этом случае становятся: s₁ = (l + 2G)e₁ + le₂.

 

 

УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНЫХ И РЕАЛЬНЫХ

ЖИДКОСТЕЙ

1. Простейшей механической моделью сплошной среды является модель идеальной жидкости, для которой характерно отсутствие сопротивления (сил трения) при скольжении одного слоя жидкости по другому. Отдельные части взаимодействуют только в виде нормального давления. Т.е. в любой точке идеальной жидкости касательные напряжения равны 0, а нормальные -(-р); (или через компоненты девиатора напряжений): .

Уравнением состояния дли идеальной жидкости служит зависимость плотности от давления и температуры:

(2.1)

Например, для идеального газа приемлемо уравнение Клапейрона -Менделеева:

.

Если плотность жидкости - функция только давления r = f(p), то жидкость называют БАРОТРОПНОЙ.

Когда имеет место степенная зависимость r = срⁿ, то говорят, что движение происходит при ПОЛИТРОПИЧЕСКОМ процессе.

Для капельных жидкостей, сжимаемость для которых чрезвычайно мала, в большом диапазоне изменения давления связь между плотностью и давлением линейна:

,

r₀ - плотность, соответствующая давлению р₀, К_ж - модуль объёмного сжатия, порядок которого равен 10⁴nМПа.

Экспериментальные данные и общие физические представления показывают, что при больших температурах и давлениях любая среда практически обладает свойствами идеальной жидкости.

В нормальных условиях модель идеальной жидкости широко используется при изучении движения многих жидкостей и газов вдали от твёрдых границ.

Одно из наиболее известных уравнений движения идеальной жидкости - закон Бернулли:

который гласит: При установившемся движении несжимаемой идеальной жидкости сумма геометрической, скоростной и пьезометрической высот вдоль линии тока остаётся величиной постоянной.

2. В тех случаях, когда силами трения или напряжения сдвига при движении жидкости пренебречь нельзя, используют следующую по сложности модель- вязкую ньютоновскую жидкость. Уравнениями состояния для такой жидкости, кроме уравнения (2.1) , будет:

, (2.2)

Т.е. между компонентами девиатора напряжений и скоростей деформации существует прямо пропорциональная связь.

Или, через компоненты тензоров напряжений и скоростей деформации

Например, при плоском слоистом течении жидкости вдоль оси Ох₁, когда v₁ = v₁(x₁, x₂), v₂ = v₃ = 0, нормальные и касательные напряжения равны:

Если, кроме того, жидкость несжимаема (div v = 0) и скорость v₁ не зависит от x₁ , то уравнение состояния имеет простейший вид:

Коэффициент пропорциональности m называется КОЭФФИЦИЕНТОМ ВЯЗКОСТИ ИЛИ ДИНАМИЧЕСКОЙ ВЯЗКОСТЬЮ жидкости.

Размерность коэффициента динамической вязкости [m] = [(сила× длина):(длина² ×скорость)] = [сила×время/длина²].

В системе СИ единицей вязкости является паскаль-секунда 1Па×с = 1н×с/м².

Величина 1 пуаз = 0.1 Па× с.

Динамическая вязкость воды при 20°С равна 10^-3 Па с.

Иногда пользуются отношением m/r, которое называется кинематической вязкостью и обозначается буквой n. Размерность кинематической вязкости м²/с.

Для газов и капельных жидкостей динамическая и кинематическая вязкости слабо зависят от давления, но сильно от температуры: убывают с повышением температуры, а у воздуха - растут.