Это равенство называется формулой Гаусса.

Если в поле мысленно проведён какой-либо замкнутый контур L, ограничивающий некоторую поверхность S,то линейный интеграл

называется ЦИРКУЛЯЦИЕЙ СКОРОСТИ,а вектор, определяемый в виде

,

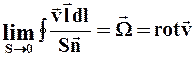называется ВИХРЕМ или РОТОРОМ скорости.

В данном случае - единичные векторы, направленные соответственно по касательной к Lи по нормали к поверхности S.

В декартовой системе координат вихрь скорости вычисляется по формуле

.

На основании теоремы Стокса имеет место равенство

.

В том случае, когда все проекции скорости могут быть определены одной функцией j(х₁, х₂, х₃, t) в виде , то есть = grad j , то говорят, что поле скоростей потенциальное, а функция j - потенциал скорости.

Проекция скорости v_l на любое направление l определяется производной dj/dl .

Необходимым и достаточным условием существования потенциальных течений являются равенства (rot = 0):

.

Следовательно, безвихревое течение потенциально.

ГИДРОСТАТИКА И ЭЛЕМЕНТЫ ДИНАМИКИ ЖИДКОСТЕЙ

 

Основным законом гидростатики является постоянство давления в любой точке покоящейся жидкости для площадок, которые проходят через точку р_х = р_у = р_z = р_n , где р_x ,р_y ,р_z , р_n - гидростатические давления на площадях, соответственно перпендикулярных к осям х, у, z , n .

Гидростатическое давление не зависит от ориентировки площадок и в разных точках жидкости может быть различным: p =f (x, y, z). Если рассмотреть равновесие элементарного объёма покоящейся жидкости плотностью r в поле сил тяжести или любой другой силы, имеющей на оси х, у, z, проекции х, у, z ускорений, соответствующих этой силе, то имеем следующую систему уравнений:

которая называется уравнениями гидростатики Эйлера.

Применительно для силы тяжести для проекций ускорений имеем: Х = 0, У = 0, Z = - g, где в последнем выражении знак минут связан с тем, что ось направлена вверх. При этом уравнения Эйлера примут вид:

Первые два уравнения указывают на то, что давление не зависит от координат хи у, то есть одинаково во всех точках любой горизонтальной плоскости, а из третьего получим

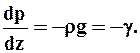
Для несжимаемой жидкости, где плотность постоянна, после интегрирования получим р + g z = С, где С - постоянная интегрирования.

Если в какой-либо точке покоящейся жидкости с координатой z₀ известно давление р₀, то С = р₀ + g z₀.

Следовательно, для произвольной координаты в общем случае имеем основное уравнение гидростатики:

р = р₀ + g (z₀ - z), или

то есть, для всех точек покоящейся однородной жидкости сумма пъезометрической р/g и геометрической z высот имеет одинаковое значение. Согласно этому соотношению для поверхности уровня (р - р₀) имеем g z = const, т.е. поверхности уровня жидкости - горизонтальные плоскости.

 

ПРАКТИЧЕСКИЕ ВЫВОДЫ ИЗ ОСНОВНОГО УРАВНЕНИЯ ГИДРОСТАТИКИ

 

1. Для сообщающихся сосудов, на поверхности однородной вязкойжидкости которых действует давление р_а, уровень жидкости в обоих сосудах будет располагаться на одной высоте.

· Если в сосудах будут находиться жидкости с разной плотностью (r₁ и r₂), то будет справедливо соотношение z₁/ z₂ = r₂/r₁ , или z₁/ z₂ = g₂/g₁, т.е. высоты уровней в сообщающихся сосудах, отсчитанные от поверхности раздела несмешивающихся вязких жидкостей, обратно пропорциональны их плотностям.

· Если к свободной поверхности одного из сообщающихся сосудов приложить избыточное давление (р_а1 > р_а2), то для вязкой однородной жидкости уровень в другом сосуде установится в положении z₂, для которого

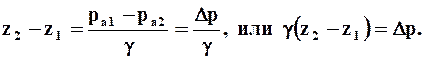
На этом принципе основаны пъезометрические приборы для измерения давлений.

· В сообщающихся сосудах вязкопластическая жидкость. В этом случае необходимый перепад давления для подъёма жидкости на высоту z₂ определится по формуле

где t₀ - динамическое напряжение сдвига; d - диаметр сообщающихся сосудов;
z₁ и z₂- высота сосудов от их общего дна.

Дополнительный член в этой формуле отражает необходимый дополнительный перепад давления для преодоления предельного напряжения сдвига.

Для скважины, заполненной однородной вязкопластичной жидкостью (буровой раствор), пусковой перепад давления на насосах необходимо определять с учётом дополнительного перепада

где L - глубина скважины; D- диаметр скважины;d₁,d₂- наружный и внутренний диаметр трубы.

2. Определение давления жидкости на ограничивающие её стенки. ОСНОВНОЕ ПРАВИЛО: составляющая давления жидкости на плоский элемент ограничивающей поверхности, параллельная горизонтальной оси, определяется как давление на проекцию этого плоского элемента, перпендикулярную к выбранной оси. При этом полная сила избыточного давления на плоскую стенку равна произведению площади стенки на избыточное давление в центре тяжести стенки. Точка приложения этой силы называется центром давления и для плоской наклонной стенки центр давления ВСЕГДА располагается НИЖЕ ЦЕНТРА ЕЁ ТЯЖЕСТИ.

3. Определение сил, действующих на поверхность погруженного в жидкость твёрдого тела. Рассмотрим цилиндрическое твёрдое тело, вертикально расположенное в жидкости. На его верхний и нижний торцы будут действовать соответственно силы: р₁ = g_ж z₁ Fи р₂ = g_ж z₂ F , где g - плотность жидкости; z₁ и z₂ - высота столба жидкости соответственно над верхним и нижним торцами; F - площадь горизонтального сечения цилиндра.

Результирующая этих сил

А = р₁ - р₂ = - g (z₂ - z₁) F = -g_ж V_ц,

где V_ц = F (z₂ - z₁)- объём цилиндра.

Для такого осесимметричного тела, как цилиндр, на боковой поверхности силы равны. В более общем случае на всякое тело объёмом D_т, погружённое в жидкость, действует выталкивающая сила, направленная вверх (знак минус) и равная по весу вытесненной им жидкости (закон Архимеда)

А = g_ж V_т .

Следует обратить внимание на то, что архимедова сила является ПОВЕРХНОСТНОЙ, то есть, действует на СМОЧЕННУЮ ПОВЕРХНОСТЬ ТЕЛА.Равнодействующая этой силы приложена в точке пересечения смоченной поверхности с вертикалью, проходящей через центр тяжести массы вытесненной жидкости в объёме погруженной части тела. Последний фактор важен для понимания природы поверхностных сил при решении задач по определению внутренних напряжений при расчёте бурильных и обсадных труб.

Архимедова сила возникает при наличии замкнутой в жидкости смоченной поверхности (в случае частично погружённого или плавающего тела смоченная поверхность замыкается горизонтальной плоскостью сечения тела в плоскости уровня жидкости).

Если тело погрузить на дно сосуда и вытеснить жидкость из зоны контакта с дном, то подъёмная сила исчезнет и, наоборот, появится сила, прижимающая тело к дну в результате действия гидростатического давления. Это является одним из объяснений ПРИХВАТОВ БУРИЛЬНОГО ИНСТРУМЕНТА, аналогичных присосу подводных лодок на грунте.

Если вес тела уравновешивается архимедовой силой для погружённой его части, то тело плавает. В противном случае оно тонет, а в общем случае тела, погружённые в жидкость, теряют в весе столько, сколько весит вытесненная им жидкость.

4. Чтобы полностью описать процессы взаимодействия при движении жидкости или тел в ней, НЕОБХОДИМО в каждой точке пространства, занятой жидкостью, знать ДАВЛЕНИЕ, ПЛОТНОСТЬ и СОСТАВЛЯЮЩИЕ СКОРОСТИ перемещения частиц жидкости:

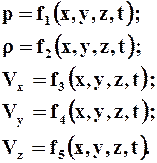
Если указанные величины являются функциями ВРЕМЕНИ, то движение называется НЕУСТАНОВИВШИМСЯ, в противном случае - УСТАНОВИВШИМСЯ. В большинстве практических задач движение жидкости неустановившееся, но когда изменение процесса во времени протекает очень медленно, для практических целей его можно считать установившимся.

5. Понятие о расходе жидкости.

Массовый расход жидкости - массовое количество жидкости, протекающее через поперечное сечение за единицу времени:

dM = vpdw,

v - скорость течения жидкости по нормали к поперечному сечению dw.

Объёмный расход жидкости - объёмное количество жидкости протекающее через поперечное сечение за единицу времени:

dQ = vdw .

Поперечное сечение плоскостью, нормальной к скорости, называют живым сечением, и общий расход через любое сечение можно определить по формуле

где - направление нормали к элементарной площадке; W - общая площадь сечения потока.

В ряде задач с целью упрощения используют понятие скорости потока, и в этом случае Q = v_срW, откуда можно определить среднюю скорость:

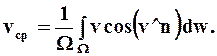
В случае установившегося течения несжимаемой жидкости средний расход не меняется во времени и при отсутствии притока или оттока расход будет одинаковым во всех сечениях по длине потока, то есть,v_срW = const,а для течения в потоке с одинаковым сечением v_ср = const.

6. Геометрические величины гидродинамики.

Смоченный периметр -периметр живого сечения, по которому периметр ЖС соприкасается со с ограничивающими стенками (для течения жидкости в кольцевом канале, образованном концентрически расположенными трубами)

c = p (D + d);

D и d - диаметры концентрически расположенных труб.

Гидравлический радиус - отношение площади ЖС потока к смоченному периметру:

.

7. Баланс механической энергии.

Для любого сечения потока жидкости полная механическая энергия складывается из потенциальной Мgz, кинетической Mv²/2 и энергии упругого состояния рV, где М - масса элемента жидкости, g - ускорение свободного падения, v - скорость этого элемента, V = M/р объём элемента. Отнеся все составляющие к единице веса, получим выражение для удельной энергии:

Помимо указанных составляющих энергия в общем случае затрачивается на преодоление сил сопротивления, обусловленных внутренним трением, удельную величину которой обозначим h_c.

Если теперь мы воспользуемся законом сохранения энергии двух сечений потока, то получим:

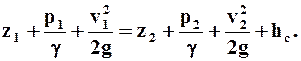
Если силы сопротивления отсутствуют, т.е. h_c = 0, это выражение соответствует уравнению Бернулли для неустановившегося потока несжимаемой вязкой жидкости:

где z - геометрический напор; v²/2g - скоростной напор; p/g - пьезометрический напор.

Для течения жидкости при наличии сил трения потери на сопротивление определяются по формуле

Для течения жидкости в горизонтальном трубопроводе постоянного сечения z₁ = z₂, v₁ = v₂, имеем

Используя гипотезу о пропорциональности сил сопротивления квадрату средней скорости потока, получим выражение

,

где l - безразмерный коэффициент сопротивления; D - расстояние между сечениями трубопровода; d - диаметр трубопровода.

Таким образом, потери давления между двумя сечениями установившегося течения жидкости при наличии сил трения в горизонтальном круглом трубопроводе определяются по формуле Дарси-Вейсбаха

.

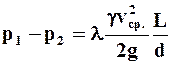Чтобы использовать формулу Дарси-Вейсбаха в практических расчётах, необходимо знать коэффициент сопротивления l, который зависит:

ü от характера течения жидкости;

ü от свойств жидкости;

ü от геометрических характеристик потока;

ü от состояния трубопровода (шероховатости) и т.д.

8. Понятие ламинарного и турбулентного режима движения.

Течение в круглой трубе, при котором жидкость движется параллельно круглым стенкам слоями, и струи её не смешиваются друг с другом, называется слоистым или ламинарным.

При увеличении скорости возникает перемешивание движущихся слоёв жидкости, которое всё более интенсифицируется с ростом скорости. Такое течение называется турбулентным или возмущённым.

Основное отличие турбулентного режима течения от ламинарного - наличие пульсаций скорости во всех направлениях потока, вследствие которого происходит интенсивное перемешивание жидкости в потоке. Турбулентное течение всегда НЕУСТАНОВИВШЕЕСЯ, даже если оно происходит под действием постоянного перепада давления в трубе.

9. Течение вязкопластичных жидкостей.

В начальный момент времени жидкость остаётся неподвижной, до тех пор, пока касательные напряжения не превысят предел текучести t₀. После того, как будет достигнут необходимый перепад давления, достаточный для преодоления сил пластичности, жидкость начнёт перемещаться, сохраняя неподвижным ядро потока радиусом r₀ , на границах ядра касательные напряжения равны, в пристенной зоне наблюдается сдвиговое течение в ламинарном режиме. Такое течение называется СТРУКТУРНЫМ. После того, как перепад давления достигнет определённой величины, ядро потока исчезает, поток некоторое время движется ламинарно, а затем переходит в турбулентный режим движения.

10. Общий случай течения несжимаемой вязкой жидкости (система уравнений Навье-Стокса + уравнение неразрывности).

В общем случае течение несжимаемой вязкой жидкости описывается системой уравнений, основывающихся на втором законе Ньютона и неразрывности потока, которые в прямоугольной системе координат имеют следующий вид:

В уравнениях Навье-Стокса первые члены отражают действие сил ИНЕРЦИИ, вторые - МАССОВОЙ (весовой) СИЛЫ ТЯЖЕСТИ, третьи - ДАВЛЕНИЯ, четвёртые - СИЛЫ ВЯЗКОГО ТРЕНИЯ на элементарный объём движущейся несжимаемой вязкой жидкости.

11. Течение между двумя безграничными горизонтальными пластинами, находящимися на расстоянии 2h , т.е. -h £ x £ h при установившемся ламинарном течении имеем:

,

или, принимая во внимание конечность перепада давления на некоторой длине L,

Используя граничное условие ПРИЛИПАНИЯ жидкости к твёрдым стенкам v = 0прих = -h и Х = h , после интегрирования получаем

что означает, что РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ - ПАРАБОЛИЧЕСКОЕ, с МАКСИМАЛЬНОЙ СКОРОСТЬЮ НА ОСИ ПОТОКА при у = 0:

При этом ОБЪЁМНЫЙ РАСХОД определяется по формуле

а СРЕДНЯЯ СКОРОСТЬ

Таким образом, для плоской щели при ламинарном течении вязкой несжимаемой жидкости расход при постоянном перепаде давления пропорционален кубу расстояния между плоскостями, или потери давления при постоянном расходе обратно пропорциональны кубу расстояния между плоскостями.

12. Ламинарное течение вязкой несжимаемой жидкости в круглой трубе (d = 2R).

т.е. для цилиндрической круглой трубы расход пропорционален четвёртой степени радиуса и потери давления РАСТУТ с уменьшением радиуса по закону четвёртой степени. Таким образом, имеем формулу Гагена-Пуазейля:

.

13. Критерий Рейнольдса.

Используя формулы Дарси-Вейсбаха и Гагена-Пуазейля можно определить величину коэффициента сопротивления l для несжимаемой вязкой жидкости при ламинарном течении:

или l = 64/Re,

где - безразмерный параметр, называемый числом или критерием Рейнольдса.

Приведённая формула для расчёта коэффициента сопротивления l справедлива в области значений Re < 2300, в которой течение для несжимаемой вязкой жидкости считается ламинарным. При дальнейшем росте числа Re режим течения переходит в турбулентный, то есть критерий Рейнольдса можно считать критерием оценки режима течения.

14. Ламинарное течение вязкопластичных жидкостей в цилиндрической круглой трубе. Картина распределения здесь более сложная:

,

где r₀ - радиус ядра потока при структурном течении, определяемом из условия r₀ = 4Lt₀/D.p.