В этом заключается гипотеза о непрерывности и сплошности среды.

Одна из основных физических величин, характеризующих жидкость, - плотность r, которая определяется выражением

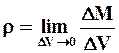где D М - масса жидкости в объёме D V.

По плотности жидкости можно определять удельный вес g, характеризующиё объёмные силы тяжести, согласно формуле

g = rg.

Принимая во внимание сжимаемость и тепловое расширение, имеем r = f(p,T), а с учётом коэффициентов сжимаемости и теплового расширения

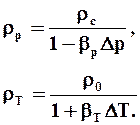
Все реальные жидкости обладают свойством сопротивляться усилиям, касательным к поверхности выделенного объёма, то есть, усилиям сдвига. Это свойство называют ВЯЗКОСТЬЮ.

Причина возникновения вязкости - диффузия молекул, сопровождающаяся переносом количества движения из одного слоя в другой и таким образом обуславливающая возникновение сил внутреннего трения в жидкости.

Рассмотрим равновесие выделенного в жидкости элементарного объёма.

В общем случае действующие силы можно разделить на поверхностные (силы трения, поверхностного натяжения, упругости) и объёмные (силы тяжести, инерции, электрического и магнитного взаимодействия).

В общем случае поверхностные силы разлагаются на нормальную и касательную составляющие.

Нормальная составляющая вызывает деформацию сжатия, её называют давлением (р).

Касательная составляющая вызывает деформацию сдвига и напряжения трения (r).

Взаимосвязь между касательными напряжениями и характеристиками движения жидкости обуславливает реологические свойства.

Если рассмотреть две параллельные площадки в движущейся жидкости, которые отстоят друг от друга на расстоянии Dh и движутся с скоростями v и v + Dv, то жидкость, подчиняющаяся закону вязкости Ньютона, имеет следующую формулу для определения касательного напряжения:

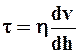где h коэффициент внутреннего трения или динамической (абсолютной) вязкости.

Наряду с коэффициентом динамической вязкости на практике используется коэффициент кинематической вязкости, определяемый по формуле

n = h/r .

Помимо жидкостей, подчиняющихся закону Ньютона (вода), в практике бурения используются жидкости, которые этому закону не подчиняются. Такие жидкости называются неньютоновскими или аномальными.

Поведение и свойства таких жидкостей изучаются реологией - разделом физической механики. В зависимости от реологического поведения жидкости можно разделить на две основные группы:

· вязкопластические жидкости, для которых

(где h - коэффициент структурной вязкости; t₀ - динамическое напряжение сдвига);

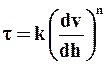· аномально вязкие жидкости, для которых

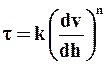( k - коэффициент консистентности, n - показатель степени).

Аномально вязкие жидкости называют:

· псевдопластичными, если они имеют n < 1,

· дилатантными (расширяющимися или растягивающимися), если n > 1,

· ньютоновскими при n = 1.

Аномально вязкие жидкости обладают свойствами твёрдого тела и жидкости, то есть проявляют упругое восстановление формы после снятия напряжения. Эти жидкости называют вязкоупругими, к ним относится модель Максвелла, или модель релаксирующего тела, для которого

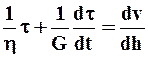где G - модуль упругости при сдвиге. Для этих тел важным параметром является величина h/G, которая называется временем релаксации и характеризует время затухания упругих напряжений в жидкости. Так в случае dv/dh

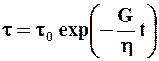где t₀- начальное упругое напряжение сдвига при мгновенном напряжении.

Из этого выражения следует, что при t = h /G напряжение в жидкости уменьшится в е раз, а при t ® ¥оно станет равным 0, то есть напряжение в теле полностью исчезнет. Чем меньше для жидкости время релаксации (G ®¥), тем слабее проявляются твёрдообразные свойства жидкостей, так как в модели такой жидкости член dt/dt ® 0, и поведение тела станет неньютоновским.

При рассмотрении неньютоновских жидкостей вводится понятие эффективной вязкости, которое

для вязкопластичных жидкостей определяется по формуле

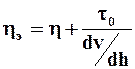а для аномально вязких жидкостей