Дополнение. Деревья.

Рис 6. Связные и несвязные графы.

Рис 5. Стандартные неплоские графы.

Рис 4. Редукция графов.

Рис 3. Плоский граф.

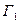
Утверждение 3.Композиция изоморфизмов и обратное изоморфизму отображение сами являются изоморфизмами.

Теорема 2. Следующие величины и свойства являются инвариантами графа , то есть сохраняются при изоморфизмах:

1). - числовершин графа;

2). - числоребер и дуг графа;

3). - число дуг графа;

4). - числоребер графа;

5). - числоциклов в графе;

6). - числоконтуров в графе;

7). - числопетель в графе;

8). - числолистьев в графе;

9). - числовершин графа степени ;

10). - числовершин графа полустепени захода ;

11). - числовершин графа полустепени исхода ;

12). Связность графа;

13). Эйлеровость, гамильтоновость и планарность графа;

Определение 27. Редукцией графа называется «стирание» вершины степени .

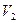
редукция

Утверждение 4.Если редуцированный граф не плоский, то и сам граф неплоский.

Утверждение 5.Если подграф не плоский, то и сам граф неплоский.

Теорема 3. Граф не является плоским тогда и только тогда, когда с помощью операций перехода к подграфу и редукции он сводится к одному из двух стандартных неплоских графов .

Определение 28. Граф называется двудольным, если множество его вершин можно разбить на два таких непересекающихся множества (доли), что и (где - пустое множество), причем – смежные только, если , а или наоборот . Если при этом каждая вершина множества соединена с каждой вершиной множества , то двудольный граф называется полным двудольным графом.

Граф – полный двудольный, а - просто полный.

Определение 29. Граф называется связным, если любые две вершины можно соединить некоторой цепью.

Связный Несвязный.

Определение 30. Связная компонента графа - это максимальный связный подграф.

Рис 7.

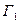
– связные компоненты.

Теорема 4. Каждая вершина графа содержится в некоторой связной компоненте.

Доказательство. Возьмем вершину графа и все вершины, с которыми данную вершину можно соединить цепью. Получим часть графа, которая и будет компонентой.

Определение 31. Сетью называется связный ориентированный граф без петель и циклов.

Вершины с полустепенью захода , называются входами, и с полустепенью исхода , называются выходами.

Определение 32. Говорят, что дуга направлена от входа к выходу, если она лежит на некотором пути от некоторого входа к некоторому выходу.

Теорема 5.Каждая сеть содержит как входы, так и выходы, причем каждая дуга сети ориентирована от входа к выходу.

Доказательство. Пусть - вершина сети. Либо - выход, либо существует такая вершина и дуга , что . Либо - выход, либо существует такая вершина и дуга , что , и т.д. В силу конечности графа получаем конечную цепочку вершин , которая обрывается на вершине , являющейся, очевидно, выходом. Аналогично доказывается существование хотя бы одного входа сети. Если - дуга сети, то от начинается цепь, заканчивающаяся выходом и в заканчивается некоторая цепь, начинающаяся на входе. Таким образом, соединяя обе цепи дугой получаем цепь от входа к выходу, содержащую . Теорема доказана.

Определение 33. Деревом называется связный неориентированный граф без петель и циклов ( в котором выделена одна вершина, называемая корнем дерева).

Теорема 6. Пусть- связный неориентированный граф с выделенной вершиной. Тогда следующие свойства эквивалентны:

1). - дерево;

2). В графе нет простых циклов (в частности петль);

3). Любые две вершины графа связаны единственной простой цепью;

4). Число ребер на 1 меньше числа вершин: = - числовершин графа.

Определение 34. Уровень корня по определению равен нулю. Число ребер цепи, соединяющей вершину с корнем называется уровнем вершины. Высотой дерева называется максимальный уровень его вершин.

Замечание. Деревья часто рисуют корнем вверх, поэтому вместо высоты дерева говорят о его глубине.

Рис 8. Дерево.- корень

На рисунке 8 изображено дерево высоты (глубины) 3. Вершины и - первого уровня, вершины , , - второго уровня, , , , - третьего уровня (листья).