Лекция № 2. Введение в теорию графов(продолжение).

Рис 1. Эйлеровы и гамильтоновы графы.

 

Эйлеров и Гамильтонов но не

гамильтонов эйлеров

 

Эйлеров (эйлеров цикл

),

но не гамильтонов.

 

Приведем доказательство негамильтоновости графа .

Вершину назовем изолированной элементарным циклом , если он содержит цепь , включающую все смежные с ней вершины, и не включающую саму вершину.

Заметим, что у гамильтонова цикла нет изолированных вершин.

Пусть существует гамильтонов цикл . Возможны следующие случаи:

1). . Тогда - изолированная вершина.

2). . Тогда - изолированная вершина.

3). . Тогда и - изолированные вершины.

Следовательно, цикл не гамильтонов, и граф также негамильтонов.

Определение 23: Отображение называетсявзаимнооднозначным, если

.

Определение 24: Взаимнооднозначное отображение множества вершин графа 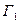на множество вершин графа и ребер (дуг) на 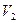, сохраняющее отношение инцидентности, называется изоморфизмом графов 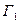и :

.

Замечание. В простом графе достаточно определить изоморфизм на множестве вершин.

Определение 25. Граф , изоморфный части графа 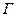, называется подграфом .

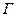Рис 2. Подграф.

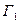
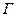
Определение 26. Граф 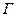называется плоским (планарным), если его можно изоморфно отобразить на граф 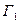, расположенный на плоскости без самопересечений.