Основные виды графов.

Рис. 1.

V ребро дуга

х₁ . . х₂ х₁ .. х₂

Отношение инцидентности R – может быть описано следующим образом. Если -ребро, то пишем , когда является концом ребра, причем каждое ребро имеет 2 конца и , возможно, совпадающие. Если -дуга, то пишем , когда – начало дуги , и , когда – конец дуги . Во всех случаях говорим, что и инцидентны.

 

Определение 2. Две вершины графа называются смежными, если они инцидентны одному ребру или дуге.

В графах на рисунке 1 вершины и – смежные, а в графе на рисунке 2 - нет.

Рис. 2.

 

Определение 3. Мультиграф – граф, две вершины которого соединены более чем одним ребром (или по крайней мере двумя дугами, идущими в одном направлении). Граф, не являющийся мультиграфом будем называть “просто граф” (простым графом).

Рис. 3.Мультиграф

 

Определение 4. Степеньвершины графа равна числу ребер (дуг) инцидентных .

Заметим, что в графе .

Определение 5. Граф называется ориентированным, если он содержит хотя бы одну дугу и не содержит рёбер..

Определение 6. Граф называется неориентированным, если он содержит только ребра.

Например, графы и – неориентированные, а – ориентированный.

Определение 7. Полустепенью исхода (захода) называется число дуг исходящих из вершины (заходящих в вершину).

Обозначения: – полустепень захода; – полустепень исхода.

.

Рис. 4.Степени и полустепени вершин.

 

Г₅

V₁ V₂ х₃

х₁ х₂ V₅

V₃ V₄

 

х₄

 

 

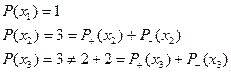
Определение 8. Петля – дуга (ребро), начало и конец которой совпадают.

Определение 9. Вершина называется изолированной, если.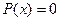

Утверждение 1. Для ориентированного графа без петель справедливы равенства

и .

Доказательство. Для ориентированного графа без петель . Отсюда следует первое равенство. Второе равенство следует из определений.

Утверждение 2. В графе без петель справедливо равенство: , где -число ребер и дуг.

Доказательство. Так как петель нет, то каждое ребро (или дуга) имеет два различных конца. Следовательно, в указанной сумме они учитываются дважды. Ч.т.д.

Утверждение 2. Для ориентированного графа без петель справедливы равенства

и .

Определение 9.Вершина называется изолированной, если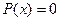

Определение 10. Вершина называется висячей (листом), если

Определение 11. Вершина называется узлом, если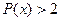

Определение 12. Граф называется однородным если все степени его вершин одинаковы.

Определение 13. Граф (простой) называется полным еслиn – число вершин

Рис. 5.Однородный и полный графы.

 

Однородный граф

 

 

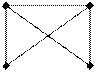Полный граф

 

Определение 14. Путь в ориентированном графе – это последовательность дуг

в которой начало следующей дуги совпадает с концом предыдущей.

Определение 15. Цепь в неориентированном графе – последовательность ребер

, в которой для каждого ребра один конец совпадает с концом предыдущего ребра, а другой конец является началом последующего ребра.

Для Г₅ последовательность – путь, а последовательность 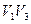– не путь.

Рис 6.Цепи в неориентированном графе .

Г6

V₁

x₂ V₂

x₁ V₃ x₃ V₅

 

V₆ V₄

x₄

 

Цепи:

Определение 16. Замкнутая цепь (путь)называется циклом (контуром).

Заметим, что цепь является замкнутой, если ее начало совпадает с концом.

В графе цепь – контур; в графе цепь – цикл, а – цикл (но не контур) !

Замечание. Если в ориентированном графе игнорировать ориентацию, то есть заменить все дуги на ребра, то получаем неориентированный граф, в котором определены цепи и циклы.

Определение 17. Путь (цепь) называется простым (простой), если каждая дуга (ребро) встречается в нем (в ней) не более 1 раза.

Определение 18. Путь (цепь) называется элементарным (элементарной), если каждая вершина встречается не более 1 раза.

Для простого графа дугу (ребро) можно записать как (соответственно, ), где – начало и конец дуги ( концы ребра).

В графе путь можно записать в виде

 

 

Определение 19: Цикл называется эйлеровым, если он содержит все ребра графа и является простым.

Определение 20: Граф называется эйлеровым если он содержит эйлеров цикл.

Определение 21: Цикл называется гамильтоновым, если он содержит все вершины графа и является элементарным.

Определение 22: Граф называется гамильтоновым если он содержит гамильтонов цикл.

Теорема 1: Если граф 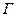Эйлеров, то все его вершины – четные.

Доказательство. Пусть - эйлеров цикл и . Началом и концом цикла можно считать некоторую вершину . Направление обхода цикла можно выбрать произвольно. Пусть при обходе цикла первый раз мы входим в вершину по некото-рому ребру и выходим по ребру . Если других ребер, инцидентных , нет, то степень вершины равна 2 и теорема доказана. Иначе, убираем ребра , и замечаем, что цикл повторно входит в вершину по некоторому ребру и выходит по ребру , так, что либо и теорема доказана, либо рассуждение можно продолжить. В результате будут исчерпаны все инцидентные ребра, что и завершает доказательство.