Множество действительных чисел.

 

Из элементарной математики известно, что совокупность рациональных и иррациональных чисел образует множество действительных чисел R. На нем определены операции:

1) Сложение: для любой пары действительных чисел а и b определено единственное число a+b, называемое их суммой, причем выполняются следующие условия:

а) a+b=b+a

b) a+(b+c)=(a+b)+c

c) существует число 0 такое, что а+0=а для любого а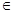R

d) 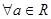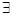противоположное число –а, для которого а+(-а)=0.

2) Умножение: 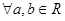определено единственное число ab, называемое их произведением, такое, что выполняются следующие условия:

а) ab=ba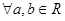

b) a(bc)=(ab)c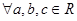

c) существует число 1 такое, что а·1=а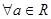

d) a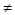0 существует обратное число 1/а, для которого а· 1/а = 1.

Связь сложения и умножения: (a + b)c = ac + bc.

 

Множество действительных чисел обладает следующими свойствами:

1) Упорядоченность - 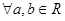либо a < b, либо a > b. При этом

а) если a < b и b < c, то a < c.

b) если a < b, то с a + c < b + c.

c) если a < b и с > 0, то ac < bc.

2) Непрерывность – для любых непустых множеств Х и Y таких, что и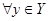

 

Подмножества множества R называют числовыми множествами.

Примеры числовых множеств:

1. Множество натуральных чисел N (1,2,3,…).
2. Множество целых чисел Z (
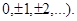
3. Множество рациональных чисел Q(числа вида m/n, где m и n – целые).