Дискретные случайные величины.

Случайные величины. Закон распределения и функция распределения дискретной случайной величины. Биномиальное распределение и распределение Пуассона.

Лекция 4.

Наряду с понятием случайного события в теории вероятности используется и более удобное понятие случайной величины.

Определение 4.1. Случайной величиной называется величина, принимающая в результате опыта одно из своих возможных значений, причем заранее неизвестно, какое именно.

Будем обозначать случайные величины заглавными буквами латинского алфавита (Х, Y,Z,…), а их возможные значения – соответствующими малыми буквами (x_i, y_i,…).

Примеры: число очков, выпавших при броске игральной кости; число появлений герба при 10 бросках монеты; число выстрелов до первого попадания в цель; расстояние от центра мишени до пробоины при попадании.

Можно заметить, что множество возможных значений для перечисленных случайных величин имеет разный вид: для первых двух величин оно конечно ( соответственно 6 и 11 значений), для третьей величины множество значений бесконечно и представляет собой множество натуральных чисел, а для четвертой – все точки отрезка, длина которого равна радиусу мишени. Таким образом, для первых трех величин множество значений из отдельных (дискретных), изолированных друг от друга значений, а для четвертой оно представляет собой непрерывную область. По этому показателю случайные величины подразделяются на две группы: дискретные и непрерывные.

 

Определение 4.2. Случайная величина называется дискретной, если она принимает отдельные, изолированные возможные значения с определенными вероятностями.

 

Определение 4.3. Случайная величина называется непрерывной, если множество ее возможных значений целиком заполняет некоторый конечный или бесконечный промежуток.

 

Для задания дискретной случайной величины нужно знать ее возможные значения и вероятности, с которыми принимаются эти значения. Соответствие между ними называется законом распределенияслучайной величины. Он может иметь вид таблицы, формулы или графика.

Таблица, в которой перечислены возможные значения дискретной случайной величины и соответствующие им вероятности, называется рядом распределения:

 

xi	x1	x2	…	xn	…
pi	p1	p2	…	pn	…

 

Заметим, что событие, заключающееся в том, что случайная величина примет одно из своих возможных значений, является достоверным, поэтому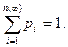

Пример. . Два стрелка делают по одному выстрелу по мишени. Вероятности их попадания при одном выстреле равны соответственно 0,6 и 0,7. Составить ряд распределения случайной величины Х – числа попаданий после двух выстрелов.

Решение. Очевидно, что Х может принимать три значения: 0, 1 и 2. Их вероятности найдены в примере, рассмотренном в лекции 3. Следовательно, ряд распределения имеет вид:

 

хi
pi	0,12	0,46	0,42

 

Графически закон распределения дискретной случайной величины можно представить в виде многоугольника распределения – ломаной, соединяющей точки плоскости с координатами (x_i, p_i).

x₁ x₂ x₃ x₄ x₅