Взаимное пересечение многогранников
Лекция 8
Построение звеньев этой линии можно производить двумя способами, комбинируя их между собой или выбирая из них тот, который в зависимости от условий задания дает более простые построения. Эти способы следующие:

а) б)
Рисунок 1. Пересечение пирамиды и призмы,
а) Пирамида и призма, б) Призма удалена из пирамиды.
Решение задачи на построение линии пересечения значительно упрощается, если одна поверхность является проецирующей.
Рассмотрим задачу, где требуется построить линию пересечения пирамиды и призмы, при этом призма является фронтально-проецирующей (рис. 2).
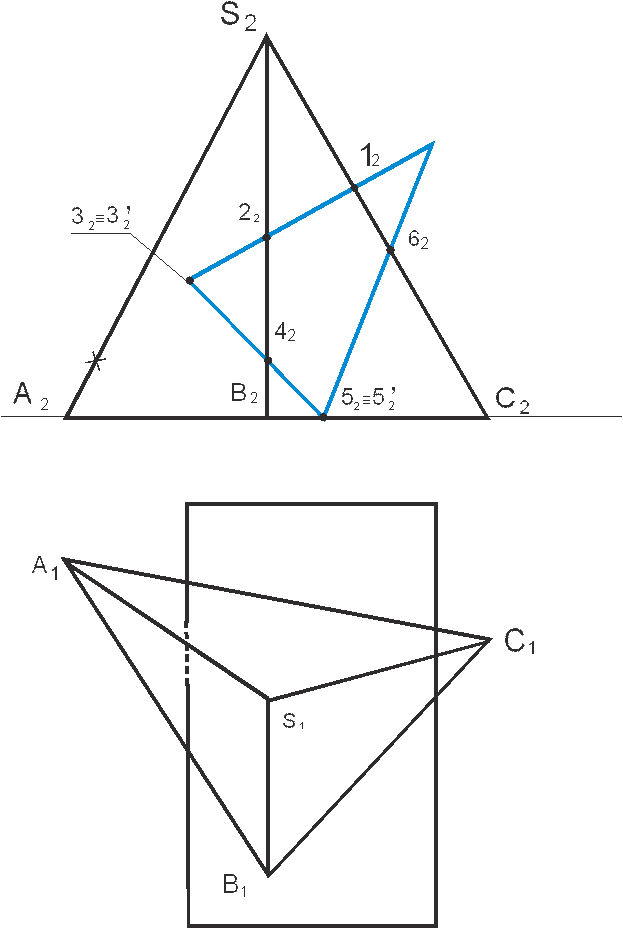
Рисунок 2. Построение линии пересечения пирамиды и призмы.
Поскольку призма является фронтально-проецирующей, фронтальная проекция линии пересечения уже определена, следовательно, требуется построить вторую горизонтальную проекцию этой линии. Определяем вершины пространственной ломаной линии на фронтальной проекции. На пресечении граней призмы с ребрами пирамиды обозначим проекции точек: 12, 22, 42, 52, 52`, 62. Ребро призы пересекает два ребра BCиAC,поэтому точка 52 совпадает с точкой 52`на фронтальной проекции. При пересечении фронтально-проецирующего ребра призмы с гранями пирамиды ASB и ASC, определяются точки 32и32`.Строим вторые горизонтальные проекции обозначенных точек. Точки 1, 5, 5`и 6 переносим на соответствующие ребра согласно аксиомам принадлежности. Для построения точек 2, 4, 3и3`воспользуемся вспомогательными прямыми, которые проведем параллельно ребрам основания. После того как построены все проекции вершин линии пересечения, соединяем их опираясь на следующее правило: точки должны принадлежать одной плоскости (грани пирамиды и призмы). Например, точка 31 принадлежит одновременно верхней и нижней граням призмы (принадлежность точек граням призмы определяем по фронтальной проекции) , соединяем ее с 21 и41, при этом отрезок 31 - 41 будет невидимым. Точку 21 соединяем с точкой 11 и так далее.