Пересечение многогранника плоскостью

 

 

Рассмотрим построение линии пересечения пирамиды с фронтально-проецирующей плоскостью S(рис. 4.). Линия пересечения на фронтальной плоскости проекций определена и проходит через точки 1₂, 2₂, 3₂ и 3₂`. Для построения второй горизонтальной проекции линии пересечения строим вторые проекции обозначенных точек, являющихся вершинами искомой ломанной, а затем последовательно их соединяем.

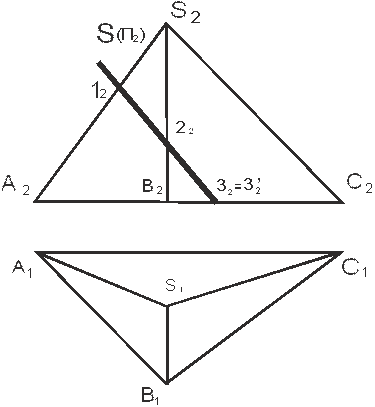
Рисунок 4. Построение линии пересечения пирамиды и проецирующей плоскости.

Рисунок 5. Наглядное изображение пересечения пирамиды и плоскости.

Пересечение многогранника с прямой.

 

Задача определения точек пересечения прямой линии с многогранником, сводится к нахождению точек пересечения прямой с плоскостями граней.

Алгоритм решения этой задачи, который рассматривался в одной из предыдущих лекций, начинается с того, что прямая заключается в проецирующую плоскость. Рассмотрим решение задачи на определение точек пересечения пирамиды и прямой m (рис. 6.).

 

 

 

 

Рисунок 6. Построение точек пересечения пирамиды и прямой. Развертка пирамиды.

 

Развертка многогранника.

 

 

1.

 

 

2.

 

 

3.

 

4.

 

 

Так как все грани многогранной поверхности изображаются на развертке в натуральную величину, построение ее сводится к определению величины отдельных граней поверхности – плоских многоугольников.

 

 

Существует три способа построения развертки многогранных поверхностей:

1. Способ нормального сечения;

2. Способ раскатки;

3. Способ треугольника (триангуляции).

При построении развертки пирамиды применяется способ треугольника. Развертка боковой поверхности пирамиды представляет собой плоскую фигуру, состоящую из треугольников – граней пирамиды и многоугольника - основания. Поэтому построение развертки пирамиды сводится к определению натуральной величины основания и граней пирамиды. Грани пирамиды можно построить по трем сторонам треугольников, их образующих. Для этого необходимо знать натуральную величину ребер и сторон основания.

Построим развертку пирамиды, продолжив рисунок 6.

Определяем натуральные величины ребер основания методом плоско-параллельного перемещения. Построение развертки начинаем с грани ВSС. Для того чтобы нанести на развертку точки пресечения пирамиды с прямой, строим на развертке линию пересечения 1-2-3.

Для построения точек пересечения M и Nна развертке воспользуемся вспомогательными прямыми, которые проведем из вершины пирамиды.