Правило сложения дисперсий
На вариацию признака влияют различные причины, факторы. Все они делятся на случайные и систематические (постоянные). Поэтому вариация может быть случайной, вызванной действием случайных причин, и систематической, обусловленной воздействием постоянных факторов. В связи с этим возникает необходимость в определении случайной и систематической вариации, их роли в общей вариации и влияния на нее.
Общая дисперсия характеризует общую вариацию признака под влиянием всех условий, всех причин, вызывающих эту вариацию, и рассчитывается следующим образом:
; 
Для определения влияния постоянного фактора на величину вариации пользуются аналитической группировкой, т.е. расчленяют по признаку-фактору всю совокупность на группы и определяют, как изменяется, варьируется общий результат под влиянием фактора, положенного в основание группировки.
Вариация между группами за счет признака-фактора, положенного в основу группировки, отражает межгрупповая вариация.
Размеры ее определяются при помощи дисперсии групповых средних.
Межгрупповая дисперсия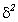 
характеризует колеблемость групповых или частных средних (
i) около общей средней 
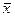и исчисляется по формулам:
; 
где xi - средняя по каждой отдельной группе;
- средняя по всей совокупности;
n - число единиц совокупности;
f - частоты или веса.
Таким образом, межгрупповая дисперсия (дисперсия групповых средних) равна средней арифметической из квадратов отклонений частных средних от общей средней.
Для определения влияния случайных факторов и их роли в общей вариации определяют дисперсию в пределах каждой группы, т.е. внутригрупповую дисперсию, а затем среднюю из внутригрупповых дисперсий.
Средняя из внутригрупповых дисперсий характеризует случайную вариацию, которая возникает по влиянием всех факторов, кроме положенного в основание группировки.
Чтобы определить её, надо рассчитать вначале внутригрупповые дисперсии по каждой группе в отдельности, а затем среднюю их них.
Между представленными видами дисперсий существует определенное соотношение: общая дисперсия равна сумме средней из внутригрупповых дисперсий и межгрупповой дисперсии.
Это равенство известно как правило сложения дисперсий, его автором является Вильгельм Лексис (1837-1914), немецкий статистик и экономист.