Параллельные прямые линии.

Взаимное положение двух прямых. Параллельные прямые. Пересекающиеся прямые. Скрещивающиеся прямые.

Взаимное расположение точки и прямой.

Если точка принадлежит прямой, то её проекции принадлежат одноименным проекциям этой прямой (аксиома принадлежности точки прямой). Из четырех предложенных на рисунке 8 точек, только одна точка С лежит на прямой АВ, так как отвечает требованиям аксиомы.

 

 

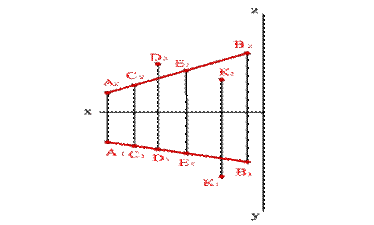
Рисунок 8. Взаимное расположение точки и прямой

 

Прямые линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися. Рассмотрим подробнее каждый случай:

Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек.

Прямы параллельны, если параллельны между собой одноименные проекции Это свойство параллельного проецирования остается справедливым и для ортогональных проекций, то есть если ABCD то A₁B₁C₁D₁; A₂B₂C₂D₂; (рис.9). В общем случае справедливо и обратное утверждение.

 

Рисунок 9. Параллельные прямые