Построение перспективы окружности (способ 8-ми точек).

 

Построение перспективы окружности может быть выполнено несколькими приемами, но наиболее простым, является прием описанного квадрата и восьми точек.

Пример 1. Построить перспективу окружности лежащей на предметной плоскости. Радиус окружности R=25 мм, высота горизонта 40 мм (рисунок 2.3).

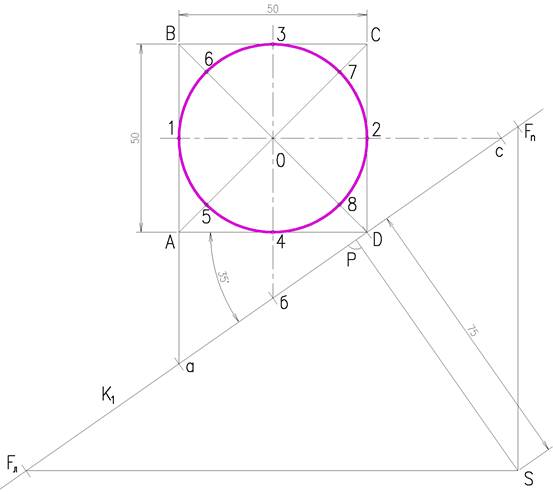
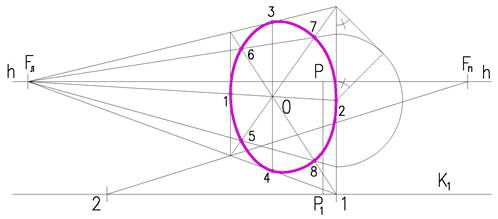
Опишем вокруг окружности с центром в т. О квадрат ABCD. Точки 1, 2, 3, 4, являются точками касания окружности к сторонам квадрата точки 5, 6, 7, 8 лежат на диагоналях квадрата.

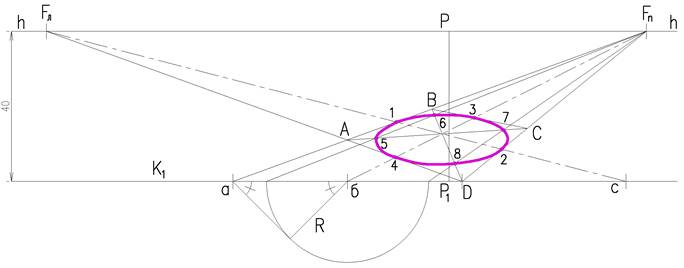
Для построения перспективы квадрата (рисунок 2.4), стороны которого не параллельны картине, достаточно использовать точки схода F_л и F_n , картинные следы осей окружности и двух сторон квадрата. Перспективы точек 1, 2, 3, 4,определяем, построив квадрат и оси окружности. Точки на диагоналях найдем, разделив половину стороны квадрата, вынесенную в картину в отношении 0,707. Для чего из точек а и б проведем под углом 45º две прямые и полученным радиусом проведем дугу до пересечения с основанием картины. Из полученных точек проведем прямые в F_n, до пересечения с диагоналями квадрата в точках 5, 6, 7, 8. Соединив, построенные восемь точек получим эллипс.

Аналогично выполняется построение окружности в любой, произвольно расположенной плоскости.

Пример 2. Дана горизонтальная проекция вертикальной окружности R=25 мм. Построить перспективу окружности при высоте горизонта 30 мм (рисунок 2.5).

На рисунке 2.6 показано построение перспективы вертикальной окружности по восьми точкам.

Мы видим, что построение выполнено аналогично примеру 1.

 

 

 

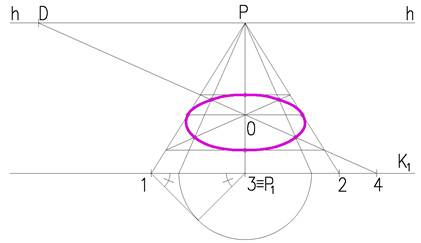
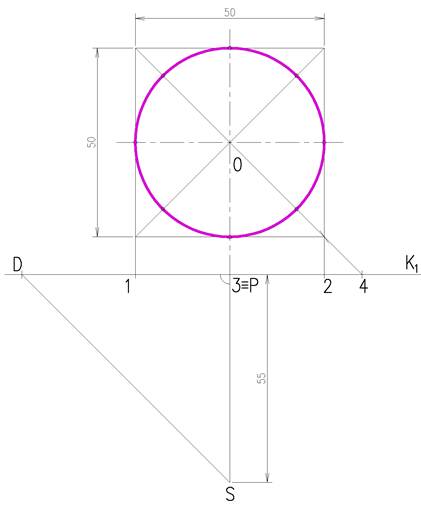Пример 3. Построить фронтальную перспективу окружности, лежащей на горизонтальной плоскости. R=25 мм, высота горизонта 40 мм (рисунок 2.7).

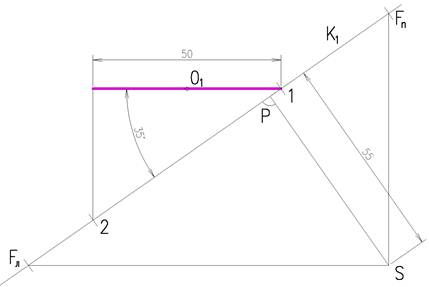
При построении фронтальной перспективы стороны квадрата перпендикулярные картине имеют точку схода Р. Две другие стороны параллельны картине и картинных следов не имеют. Поэтому, чтобы построить квадрат необходимо построить перспективу диагонали квадрата, которая имеет точку схода D – дистанционную точку (PD=SP). Остальные построения аналогичны предыдущим (рисунок 2.8).