Расстояние между объектами и мера близости

МЕТОДЫ МНОГОМЕРНОЙ КЛАССИФИКАЦИИ

В статистических исследованиях группировка первичных данных является основным приемом решения задачи классификации, а значит и основой всей дальнейшей работы с собранной информацией.

Традиционно эта задача решается следующим образом. Из множества признаков, описывающих объект, отбирается один, наиболее информативный с точки зрения исследователя, и производится группировка в соответствии со значениями данного признака. Если требуется провести классификацию по нескольким признакам, ранжированным между собой по степени важности, то сначала производится классификация по первому признаку, затем каждый из полученных классов разбивается на подклассы по второму признаку, и т.д. Подобным образом строится большинство комбинационных статистических группировок.

В тех случаях, когда упорядочить классификационные признаки не предоставляется возможным, применяется наиболее простой метод многомерной группировки – создание интегрального показателя (индекса),функционально зависящего от исходных признаков, с последующей классификацией по этому показателю.

Развитием этого подхода является вариант классификации по нескольким обобщающим показателям (главным компонентам),полученным с помощью методов факторного анализа.

При наличии нескольких признаков (исходных или обобщенных) задача классификации может быть решена методами кластерного анализа, которые от других методов многомерной классификации отличаются отсутствием обычных выборок, т.е. априорной информации о распределении генеральной совокупности, которая представляет собой вектор Х.

Различия между схемами решения задач классификации во многом определяется тем, что понимают под понятиями «сходство» и «степень сходства».

После того, как сформулирована цель работы, необходимо попытаться определить критерии качества, целевую функцию, значения которой позволят сопоставить различные схемы классификации.

В экономических исследованиях целевая функция, как правило, должна минимизировать некоторый параметр, определенный на множестве объектов (например, целью классификации оборудования может явиться группировка, минимизирующая, совокупность затрат времени и средств на ремонтные работы).

В случаяx, когда формализовать цель задачи не удалось, критерием качества классификации может служить возможность содержательной интерпретации найденных групп.

Рассмотрим следующую задачу. Пусть исследуется совокупность n объектов, каждый из которых характеризуется по k замеренным но нем признакам X. Требуется разбить эту совокупность на однородные в некотором смысле группы (классы). При этом практически отсутствует априорная информация о характере распределения измерений Х внутри классов.

Полученные в результате разбиения группы обычно называют кластерами (от англ. cluster – группа элементов, характеризуемых каким – либо общим свойством), а также таксонами (от англ. taxon- систематизированная группа любой категории) и образами. Методы нахождения кластеров называется кластер - анализом (соответственно численной таксономией или распознаванием образов с самообучением).

При этом с самого начала необходимо четко представить, какая из двух задач классификации подлежит решению. Если решается обычная задача типизации, то совокупность наблюдений разбивают на сравнительно небольшое число областей группирования (например, интервальный вариационный ряд в случае одномерных наблюдений), так, чтобы элементы одной такой области по возможности находились друг от друга на небольшом расстоянии.

Решение другой задачи типизации заключается в определение естественного расслоения исходных наблюдений на четко выраженные кластеры, лежащие друг от друга на некотором расстоянии.

Если первая задача типизации всегда имеет решение, то при второй постановке может оказаться, что множество исходных наблюдений не обнаруживает естественного расслоения на кластеры, т.е образует один кластер.

Несмотря на то что многие методы кластерного анализа довольны элементарны, применение методов кластерного анализа стало возможным только в 80-е годы с возникновением и развитием вычислительной техники. Это объясняется тем, что эффективное решение задачи поиска кластеров требует большего числа арифметических и логических операций.

Рассмотрим три различных подхода к проблеме кластерного анализа: эвристический, экстремальный и статистический.

Эвристический подходхарактеризуется отсутствием формальной модели изучаемого явления и критерия для сравнения различных решений. Его основой является алгоритм, построенный исходя из интуитивных соображений.

При экстремальном подходе также не формулируется исходная модель, а задается критерий, определяющий качество разбиения на кластеры. Такой подход особенно полезен, если цель исследования четко определена. В этом случае качество разбиения может измеряется эффективностью выполнения цели.

Основой статистического подхода решения задачи кластерного анализа является вероятностная модель исследуемого процесса. Статистический подход особенно удобен для теоретического исследования проблем, связанных с кластерным анализом. Кроме того, он дает возможность ставить задачи, связанные с воспроизводимостью результатов кластерного анализа.

Рассмотрим формы представления исходных данных и определение мер близости.

В задачах кластерного анализа обычной формой представления исходных данных служит прямоугольная таблица, каждая строка которой представляет результат измерения k рассматриваемых признаков на одном из обследованных объектов:

.

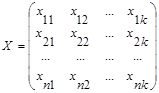В конкретных ситуациях может представлять интерес как группировка объектов, так и группировка признаков. В случаях, когда разница между этими двумя задачами несущественна, например при описании некоторых алгоритмов, мы будем пользоваться только термином «объект», подразумевая в этом понятии и «признак».

Числовые значения, входящие в матрицу Х, могут соответствовать трем типам переменных: количественным, ранговым и качественным. Количественныепеременные обладают свойством упорядоченности и над ними можно производить арифметические операции. Значения ранговыхпеременных тоже упорядочены, и их можно пронумеровать натуральными числами. Однако использование этих чисел в арифметических операциях будет некорректным. Качественныминазываются переменные, принимающие 2 (дихотомные) или более значения. Этим значением также можно поставить в соответствии некоторые числа, которые, однако, не будут отражать какой – либо упорядоченности значений качественной переменной. Исключением являются дихотомные переменные, два значения которых (как правило, они обозначаются числами 0 и 1) можно считать упорядоченными.

Желательно, чтобы таблица исходных данных соответствовала одному типу переменных. В противном случае разные типы переменных стараются свести к какому – то одному типу переменных. Например, все переменные можно свести к дихотомным, используя следующую процедуру. Количественные переменные переводят в ранговые, разбивая области значений количественной переменной на интервалы, которые затем нумеруются числами натурального ряда. Ранговые переменные автоматически становятся качественными, если не учитывать упорядоченности их значений. Что касается качественных переменных, то каждому из возможных ее значений приходится сопоставлять дихотомную переменную, которая будет равна 1, если качественная переменная приняла данное значение, и 0 – в противном случае.

Отметим, что форма записи исходных данных, их сведения к одному типу, возможность использования только части данных и т.п., играют определенную роль при оценке практической эффективности вычислительного комплекса, предназначенного для решения задач классификации.

Матрица X не является единственным способом представления исходных данных в задачах кластерного анализа. Иногда исходная информация задана в виде квадратной матрицы

R=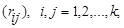

элемент r_ij которой определяет степень близости i-го объекта к j-му.

Большинство алгоритмов кластерного анализа либо полностью исходит из матрицы расстояний (или близостей), либо требует вычисления отдельных ее элементов, поэтому, если данные представлены в форме Х, то первым этапом решения задачи поиска кластеров будет выбор способа вычисления расстояний или близости между объектами или признаками

(в этом отношении различие между объектами и признаками является существенным).

Относительно просто отделяется близость между признаками. Как правило, кластерный анализ признаков преследует те же цели, что и факторный анализ – выделение групп связанных между собой признаков, отражающих определенную сторону изучаемых объектов. В этом случае мерами близости служат различные статистические коэффициенты связи.

Если признаки количественные, то можно использовать оценки обычных парных выборочных коэффициентов корреляции r_ij, i, j =1,2,…,k. Однако, коэффициент корреляции измеряет только линейную связь, поэтому если связь нелинейна, то следует использовать корреляционное отношение, либо произвести подходящее преобразование шкалы признаков.

Существуют также различные коэффициенты связи, определенные для ранговых, качественных и дихотомных переменных.

 

 

Наиболее трудным и наименее формализованным в задаче классификация является определение понятия однородности объектов.

В общем случае понятие однородности объектов задается либо введением правила вычислений расстояния 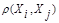между любой парой исследуемых объектов (Х₁,Х₂,..,Х_n), либо заданий некоторой функций, характеризующей степень близости i-го и j-го объектов. Если задана функция 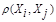, то близкие с точки зрения этой метрики объекты считаются однородными, принадлежащие одному классу. При этом необходимо сопоставлять 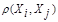с некоторым пороговым значением, определенным в каждом конкретном случае по-своему.

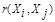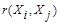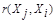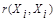
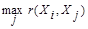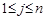Аналогично используются и мера близости , при задании которой надо помнить о необходимости выполнения условий симметрии =; максимального сходства объекта с самим собой при , и монотонного убывания 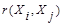по 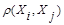, т.е. из 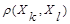≥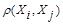должно следовать неравенство ≤.

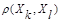Выбор метрики или меры близости является узловым моментом исследования, от которого в основном зависит окончательный вариант разбиения объектов на классы при данном алгоритме разбиения. В каждом конкретном случае этот выбор должен производиться по – своему в зависимости от целей исследования, физической и статистической природы вектора наблюдений X, априорных сведений о характере вероятностного распределения Х.

Рассмотрим наиболее часто используемые расстояния и меры близости в задачах кластерного анализа.

 

Расстояние махаланобиса (общий вид)

В случае зависимости компонент 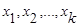вектора наблюдений Х и их различной значимости в решении вопроса квалификации обычно используют обобщенное (взвешенное) расстояние Махаланобиса, задаваемое формулой

, (7.1)

где 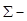ковариационная матрица генеральной совокупности, из которой извлекаются наблюдения;

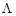- некоторая симметрическая неотрицательно-определенная матрица «весовых» коэффициентов, которая чаще всего выбирается диагональной.

Следующие три вида расстояний являются частными случаями метрики ρ_0.

 

ОБЫЧНОЕ ЭВКЛИДОВОЕ РАССТОЯНИЕ

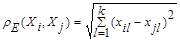(7.2)

где 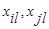- величина l-й компоненты у i-го (j-го) объекта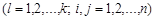

Использование этого расстояния оправдано в случаях, если:

а) наблюдения берутся из генеральных совокупностей, имеющих многомерное нормальное распределение с ковариационной матрицей вида 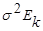, т.е компоненты Х взаимно независимы и имеют одну и ту же дисперсию;

б) Компоненты вектора наблюдения Х однородны по физическому смыслу и одинаковы важны для классификации;

в) признаковое пространство совпадает с геометрическим пространством.

Естественно с геометрической точки зрения и содержательной интерпретации евклидовое расстояние может оказаться бессмысленным, если его признаки имеют разные единицы измерения. Для приведения признаков к одинаковым единицам прибегают к нормировке каждого признака путем деления центрированной величины на среднее квадратическое отклонение и переходят от матрицы Х к нормированной матрице с элементами

 

где 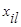- значение l-го признака i-го объекта;

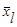-среднее арифметическое значениеl-го признака;

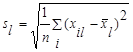-среднеквадратическое отклонениеl-го признака;

Однако это операция может привести к нежелательным последствиям. Если кластеры хорошо разделены по одному признаку и не разделены по другому, то после нормировки дискриминирующие возможности первого признака будут уменьшены в связи с увеличением «шумового» эффекта второго.

 

 

«ВЗЕШЕННОЕ» ЕВКЛИДОВО РАССТОЯНИЕ

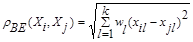(7.3)

применяется в случаях, когда каждой компоненте 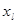вектора наблюдений Х удается приписать некоторый «вес» w_l, пропорциональной степени важности признака задачи классификации. Обычно принимают 0≤wt≤1 где l=1, 2,…,k.

Определение «весов», как правило, связано с дополнительными исследованиями, например, организацией опроса экспертов и обработкой их мнений. Определение весов w_l только по данным выборки может привести к ложным выводам.