Количественные измерения информации на основе формулы Шеннона
АЛГОРИТМ КАК МЕТОД ПРЕОБРАЗОВАНИЯ ИНФОРМАЦИИ. ТИПЫ АЛГОРИТМОВ. НОРМАЛЬНЫЙ АЛГОРИТМ МАРКОВА.
ЛЕКЦИЯ №8
Известно, что впервые числовые оценки поэтического текста выполнялись известным русским математиком А.А. Марковым в начале XX столетия. Сущность этих оценок сводилась к следующему: из романа А.С. Пушкина «Евгений Онегин» составлялся список всех слов, например, на начальную букву «а», затем, исходя из этого списка, подсчитывалась вероятность появления всех букв русского алфавита на втором месте после буквы «а», далее на третьем месте и т.д. По такой же схеме анализировались списки слов на другие начальные буквы.
Вероятностный процесс появления букв алфавита в определенных позициях слова А.А. Марков назвал случайным процессом, начинающимся с некоторого начального состояния. В указанном случае начальное состояние – это список слов на начальную букву «а». В настоящее время в теории массового обслуживания такие случайные процессы стали называться цепями Маркова.
Следует заметить, что при анализе указанного произведения А.А. Маркову удалось накопить такой фактический материал по так называемым вероятностям перехода, который и по сей день служит надежной экспериментальной проверкой различных теорий массового обслуживания.
После исследований А.А. Маркова интерес к информационным измерениям текстов естественного языка возобновился только с установлением К.Э. Шенноном следующей формулы для приближенных вычислений количественной меры информации (см. ранее)
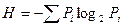 , (1)
, (1)
где через Pi обозначена вероятность или частота i-го события, а суммирование производится по всем значениям Рi.
Величина Н измеряется в битах и ее часто называют энтропией информации. Формулу (1) стали применять при анализе кодов, используемых при передаче сообщений, составленных на каком-либо естественном языке.
Сам К. Шеннон не дал строгих правил вычисления частоты рi применительно к различным ситуациям. Некоторые исследователи под рi стали подразумевать частоты появления букв алфавита в текстах естественного языка, а величину Н стали трактовать как энтропию текста.
Для применения формулы (1) в частотных измерениях литературных текстов необходимо ей придать иное толкование по сравнению с толкованием в теории передачи сообщений.
Действительно, для определения количественной меры детерминированной информации используется комбинаторная формула
 , (2)
, (2)
связывающая длину слова m с количеством N слов этой длины, составленных из букв двоичного алфавита. Американский исследователь Л. Хартли в 1928г. отождествил максимальное количество информации Н с длиной слова m, то есть
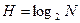 , (3)
, (3)
Предположим, что имеет место N слов как объем некоторой статистической выборки, состоящей из нескольких групп слов, а также, что в пределах каждой группы слова имеют одинаковую длину [45]. Обозначим через ni объем каждой группы слов, тогда очевидно, что
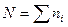
По формуле (2) вычислим длину слова из группы n1, после будем иметь
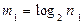 , (4)
, (4)
Теперь вычислим разность левых и правых частей в формулах (2) и (4):
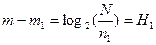 (5)
(5)
Из (5) получается, что Н1 суть длина не идентифицированных слов.
Аналогично можно составить следующие соотношения
 …,
…, 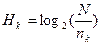 (6)
(6)
Далее составим среднюю статистическую сумму
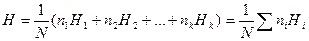 ,
,
которую с учетом (5)-(6) перепишем так:
 (7)
(7)
Если объем каждой группы слов равен единице (n1=1) и число групп k равно N, то формула (7) переходит в формулу Хартли (3). В общем случае обозначим через рi частоту появления слов i-ой группы, которую определим общеизвестным способом
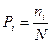 (8).
(8).
Теперь после подстановки (8) в (7), получим формулу Шеннона (1).
Этот вывод формулы Шеннона впервые выполнен в [45], из которого следует, что Н есть статистическая средняя длина всех неидентифицированных слов, входящих в данную выборку N, а рi – частота, или вероятность появления этих слов.
С позиции исчисленческой части языка любой текст – это множество (набор) слов. Слова образуют группы слов по какому-либо признаку. В качестве такого признака можно выбрать, например, начальную букву слова. Если число всех слов в тексте обозначить через N1, а число слов на конкретную начальную букву – через ni, то можно определить величину
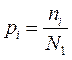 , (9),
, (9),
которую назовем частотой появления слова на данную i-ю букву. В число ni будем включать и слова, состоящие из одной буквы.
По набору частот pi можно вычислить энтропию информации по формуле Шеннона
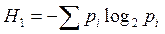 (10)
(10)
Напомним, что величина Н1 известна также как количественная мера информации, и она измеряется в битах.
Впервые в [7] этот критерий был использован для количественных оценок поэтических текстов Н. Рубцова.Там же описана подробная технология расчета pi и энтропии Н1 на основе пакета Microsoft Office 97 применительно к поэтическим текстам Н.Рубцова.
После вычислений получим гистограмму. Такая гистограмма соответствует нормальной кривой распределения, для которой имеют физический смысл такие характеристики положения, как математическое ожидание 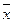 и среднее квадратичное отклонение σ. Для вычисления этих величин в математической статистике имеют место следующие формулы
и среднее квадратичное отклонение σ. Для вычисления этих величин в математической статистике имеют место следующие формулы
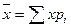 ;
; 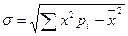
Для стихотворения Рубцова эти числа оказались равными 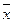 =14,2586, σ =4,5934.
=14,2586, σ =4,5934.