Положение прямой линии относительно плоскостей проекций
В зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения.
1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.9).


Рисунок 9. Прямая общего положения
2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:
2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.10). Для любой пары точек горизонтали должно быть справедливо равенство
zA=zB Þ A2B2//0x; A3B3//0y Þ xA–xB#0, yA–yB#0, zA–zB=0.
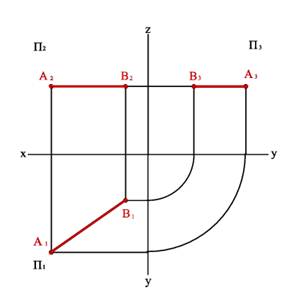

Рис. 10. Горизонтальная прямая (горизонталь)
2.2. Прямые параллельные фронтальной плоскости проекций называютсяфронтальными или фронталями (рис.11).
yA=yBÞ A1B1//0x, A3B3//0z Þ xA–xB#0, yA–yB=0, zA–zB#0.

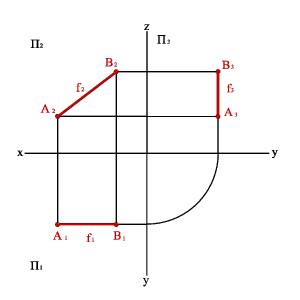
Рис. 11. Фронтальная прямая
2.3. Прямые параллельные профильной плоскости проекций называются профильными (рис.12).
xA=xBР A1B1//0y, A2B2//0zР xA–xB=0, yA–yB#0, zA–zB#0.
Различают восходящую и нисходящую профильные прямые. Первая по мере удаления от зрителя поднимается, вторая - понижается.


Рис. 12. Профильная прямая
3. Прямые перпендикулярные плоскостям проекций, называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают:
3.1. Фронтально проецирующая прямая - АВ (рис. 13)
xA–xB=0ü yA–yB#0ý zA–zB=0þ,
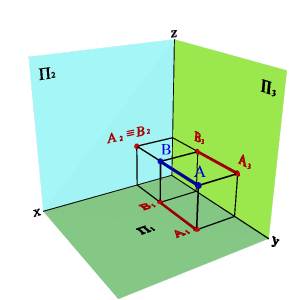
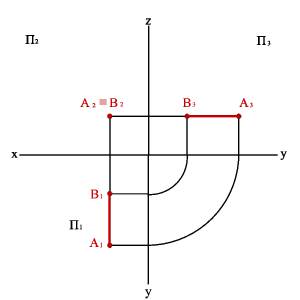
Рис. 13. Фронтально проецирующая прямая
3.2. Профильно проецирующая прямая - АВ (рис.14)
xА–xB#0ü yА–yB=0ý zА–zB=0þ,


Рисунок 14. Профильно-проецирующая прямая
3.3. Горизонтально проецирующая прямая - АВ (рис.15)
xА–xВ=0ü yА–yВ=0ý zА–zВ#0þ.

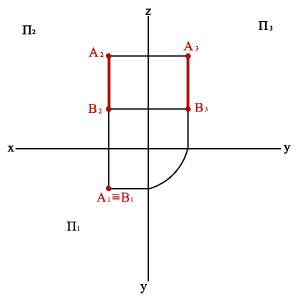
Рисунок 15. Горизонтально-проецирующая прямая
4. Прямые параллельные биссекторным плоскостям (рис. 16)
АВ //S1бис Þ xA–xB=0; zB–zA=yB–yA; СD//S2бис Þ xС–xD=0; zD–zC=yC–yD.
Биссекторной плоскостью называется плоскость проходящая через ось 0х и делящая двухгранный угол между плоскостями проекций П1 и П2 пополам. Биссекторная плоскость проходящая через 1 и 3 четверти называется первой биссекторной плоскостью (S1бис) ,а через 2 и 4 четверти - второй (S2бис).
5. Прямые перпендикулярные биссекторным плоскостям (рис. 16)
АВ^S2бис Þ xA–xB=0; zB–zA=yВ–yА;. СD^S1бис Þ xС–xD=0;zD–zC=yC–yD


Рис. 16. Прямые параллельные и перпендикулярные биссекторным плоскостям