для студентов специальности
Тесты по дисциплине «Эконометрика»
«Финансы», «Учет и аудит», «Экономика», «Менеджмент»
<question>Что такое число степеней свободы?
<variant> Число независимых отклонений для образования данной суммы квадратов
<variant> Число независимых отклонений для образования данной суммы
<variant> Число образований данной суммы квадратов
<variant> Число независимых отклонений суммы квадратов
<variant> Число отклонений суммы квадратов
<question>Число степеней свободы связано с:
<variant> числом единиц совокупности n и числом определяемых констант
<variant> числом единиц совокупности n и числом переменных
<variant> числом переменных и числом определяемых констант
<variant> числом единиц совокупности n и числом слагаемых, образовывающих сумму
<variant> числом слагаемых, образовывающих сумму и числом определяемых констант
<question>Число степеней свободы для общей суммы квадратов при линейной регрессии равно
<variant> n-1
<variant> n-2
<variant> n
<variant> n+1
<variant> n+2
<question>Число степеней свободы остаточной суммы квадратов при линейной регрессии составляет
<variant> n-2
<variant> n-1
<variant> n
<variant> n+1
<variant> n+2
<question>Какое из уравнений регрессии целесообразно применять для характеристики зависимости урожайности от количества внесенных удобрений
<variant> параболическая
<variant> гиперболическая
<variant> показательная
<variant> линейная
<variant> степенная
<question>Зависимость потребления электроэнергии от объема продукции удобно выразить регрессией вида:
<variant> линейная
<variant> гиперболическая
<variant> показательная
<variant> параболическая
<variant> степенная
<question>Зная,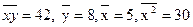 
. Найдите b для у = а + bх.
<variant> 0,4
<variant> 48
<variant> 30
<variant> 0
<variant> 0,28
<question>Какая из регрессий является нелинейной по оцениваемым параметрам:
<variant>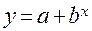 
<variant>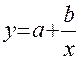 
<variant>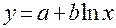 
<variant>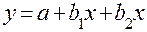 
<variant>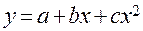 
<question>Метод наименьших квадратов используется:
<variant> для оценки параметров регрессии
<variant> для оценки параметров регрессии нелинейных по параметрам
<variant> для нахождения теоретических значений у
<variant> для оценки значений х
<variant> для нахождения фактических значений у
<question>Тесноту связи изучаемых явлений оценивает:
<variant> коэффициент корреляции r
<variant> параметр a
<variant> коэффициент b
<variant> индекс корреляции
<variant> средняя ошибка аппроксимации
<question>Оценка качества построенной модели определяется с помощью
<variant> коэффициента детерминации
<variant> коэффициент b
<variant> коэффициент корреляции r
<variant> коэффициента вариации
<variant> коэффициента эластичности
<question>Средняя ошибка апроксимации—это:
<variant>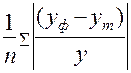 
*100%
<variant> разность между фактическим значением у и теоретическим значением у
<variant>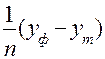 
*100%
<variant> 
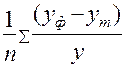*100%
<variant>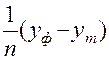 
<question>Коэффициент, показывающий насколько % в среднем по совокупности изменится результат у от своей средней величины при изменении фактора х на 1% от своего среднего значения, называется
<variant> коэффициент эластичности
<variant> коэффициент детерминации
<variant> коэффициент вариации
<variant> средняя ошибка аппроксимации
<variant> коэффициент корреляции
<question>Общая сумма квадратов отклонений—это
<variant>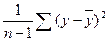 
<variant>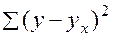 
<variant>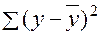 
<variant>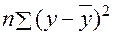 
<variant>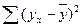 
<question>Факторная сумма квадратов отклонений
<variant>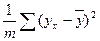 
<variant>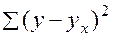
<variant>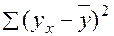 
<variant>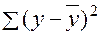
<variant>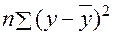
<question>Остаточная сумма квадратов отклонений
<variant>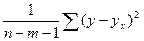 
<variant>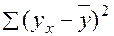
<variant>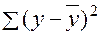
<variant>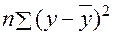
<variant>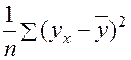 
<question>Оцените тесноту линейной связи при помощи коэффициента корреляции, если σх=48, σу=24, b = 0,28.
<variant> 0,56;
<variant> 48;
<variant> 0,28
<variant> 24;
<variant> 0.
<question>Прогнозируемое значение результативного признака определяется путем:
<variant> подстановки в уравнение регрессии
<variant> нахождения коэффициента корреляции
<variant> нахождения ошибки аппроксимации
<variant> метода наименьших квадратов
<variant> нахождения коэффициента эластичности
<question>Допустимый предел значений средней ошибки аппроксимации:
<variant> не более 10%
<variant> не менее 11-15%
<variant> 10-20%
<variant> не менее 30%
<variant> не более 30%
<question>Средние коэффициенты эластичности для линейной множественной регрессии определяются по формуле:
<variant>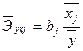 
<variant>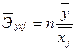 
<variant>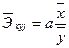 
<variant>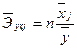 
<variant>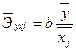 
<question>Коэффициент эластичности для линейной регрессии равен:
<variant>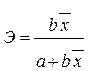 
<variant>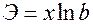 
<variant>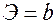 
<variant>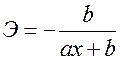 
<variant>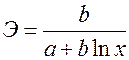 
<question>Коэффициент эластичности для (равносторонняя гипербола) гиперболической регрессии равен:
<variant>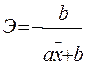 
<variant>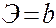 
<variant> 
<variant>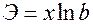
<variant>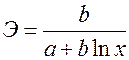
<question>Коэффициент эластичности для показательной регрессии равен:
<variant>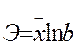 
<variant>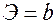
<variant>
<variant>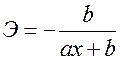
<variant>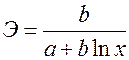
<question>Коэффициент эластичности для степенной регрессии равен:
<variant>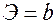
<variant>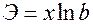
<variant>
<variant>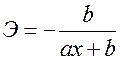
<variant>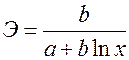
<question>Корреляционная связь—это
<variant> связь, при которой изменение среднего значения результативного признака обусловлено изменением факторным признаком
<variant> зависимость, проявляющаяся не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений
<variant> связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака
<variant> связь, при которой изменение среднего значения результативного признака обусловлено изменением факторным признаком
<variant> признаки, изменяющиеся под действием факторных признаков
<question>Временной ряд-это
<variant> последовательность измерений в последовательные моменты времени
<variant> числовые значения случайных величин
<variant> таблица значений случайной величины
<variant> интервальный ряд
<variant> ряд значений признака
<question>Лаг – это
<variant> число периодов, по которым рассчитывается коэффициент автокорреляции
<variant> сезонное колебание уровней временных рядов.
<variant> циклическое поведение уровней временных рядов.
<variant> последовательность уровней временных рядов.
<variant> Все ответы верны
<question>Аддитивная модель – модель вида:
<variant> Y=T+S+E
<variant> Y=T-(S*E)
<variant> Y=T*S*E
<variant> Y=T+(S*E)
<variant> Y=T/(S+E)
<question>Дисперсия—это
<variant> величина, вычисляемая как средний квадрат отклонений вариантов от их средней величины
<variant> разность между максимальным и минимальным значениями признака в изучаемой совокупности
<variant> последовательность уровней временных рядов.
<variant> связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака
<variant> зависимость, проявляющаяся не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений
<question>Определите качество модели при помощи средней ошибки аппроксимации, если n =20, ΣАi=90.
<variant> 4,5%
<variant> 12%
<variant> 25
<variant> 25%
<variant> 0
<question>Мультипликативная модель – модель вида:
<variant> Y=T*S*E
<variant> Y=T-(S*E)
<variant> Y=T+S+E
<variant> Y=T+(S*E)
<variant> Y=T/(S+E)
<question>Корреляция—это
<variant> статистическая зависимость между случайными величинами, не имеющая строго функционального характера, при котором изменение одной из случайных величин приводит к изменению математического ожидания другой
<variant> зависимость, проявляющаяся не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений
<variant> признаки, обусловливающие изменения других, связанных с ними признаков
<variant> связь, при которой изменение среднего значения результативного признака обусловлено изменением факторным признаком
<variant> признаки, изменяющиеся под действием факторных признаков
<question>Факторные признаки—это
<variant> признаки, обусловливающие изменения других, связанных с ними признаков
<variant> зависимость, проявляющаяся не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений
<variant> совокупность отобранных для обследования единиц
<variant> совокупность единиц, из которой производится отбор
<variant> признаки, изменяющиеся под действием факторных признаков
<question>Дана таблица значений. Найти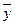 
| N | x | Y |
<variant> 4,33
<variant> 5
<variant> 76,9
<variant> 8
<variant> 2
<question>Дана таблица значений. Найти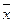 
| N | x | Y |
<variant> 7,67
<variant> 2
<variant> 4
<variant> 8
<variant> 7
<question>Если в модели парной линейной регрессии 
Чему равен параметр а?
<variant> 2,12
<variant> 3,32
<variant> –8,5
<variant> 0,25
<variant> –0,25
<question>Результативный признак—это
<variant> признаки, изменяющиеся под действием факторных признаков
<variant> зависимость, проявляющаяся не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений
<variant> признаки, обусловливающие изменения других, связанных с ними признаков
<variant> совокупность отобранных для обследования единиц
<variant> совокупность единиц, из которой производится отбор
<question>Корреляционный анализ—это
<variant> метод количественного измерения тесноты связи между варьирующими признаками
<variant> выбор типа модели, установление степени влияния независимых переменных на зависимую и определение расчетных значений зависимой переменной
<variant> квадрат линейного коэффициента корреляции
<variant> определение некоторых неизвестных уровней внутри данного ряда динамики
<variant> показатель интенсивности изменения уровня ряда, выраженный в процентах
<question>Регрессионный анализ—это
<variant> выбор типа модели, установление степени влияния независимых переменных на зависимую и определение расчетных значений зависимой переменной
<variant> метод количественного измерения тесноты связи между варьирующими признаками
<variant> квадрат линейного коэффициента корреляции
<variant> определение некоторых неизвестных уровней внутри данного ряда динамики
<variant> показатель интенсивности изменения уровня ряда, выраженный в процентах
<question>Найти среднее арифметическое чисел 1,2,3,4.
<variant> 5/2
<variant> 5
<variant> 1/2
<variant> 2
<variant> 2/5
<question>Линейный коэффициент детерминации—это
<variant> квадрат линейного коэффициента корреляции
<variant> выбор типа модели, установление степени влияния независимых переменных на зависимую и определение расчетных значений зависимой переменной
<variant> метод количественного измерения тесноты связи между варьирующими признаками
<variant> определение некоторых неизвестных уровней внутри данного ряда динамики
<variant> показатель интенсивности изменения уровня ряда, выраженный в процентах
<question>Общая дисперсия:
<variant> измеряет вариацию признака по всей совокупности под влиянием всех факторов
<variant> систематическая вариация результативного порядка
<variant> случайная вариация, обусловленную влиянием неучтенных факторов
<variant> определение некоторых неизвестных уровней внутри данного ряда динамики
<variant> показатель интенсивности изменения уровня ряда, выраженный в процентах
<question>Определите качество модели при помощи средней ошибки аппроксимации, если n =25, ΣАi=95.
<variant> 3,8%
<variant> 12%
<variant> 25
<variant> 25%
<variant> 0
<question>Для того, чтобы уравнение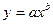 
свести к линейному, необходимо
<variant> Прологарифмировать обе части уравнения
<variant> Произвести замену 
<variant> Произвести замену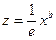 
<variant> Проинтегрировать обе части
<variant> Все ответы верны
<question>Определите качество модели при помощи средней ошибки аппроксимации, если n =12, ΣАi=68,9.
<variant> 5,7%
<variant> 12
<variant> 34,5%
<variant> 3,85
<variant> 0
<question>Укажите уравнение множественной линейной регрессии
<variant> 
<variant>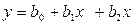 
<variant>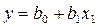 
<variant>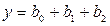 
<variant>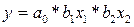 
<question>Как обычно в эконометрике называют независимую переменную y?
<variant> Результативным признаком
<variant> Значением регрессии
<variant> Фактором
<variant> Переменной
<variant> Нет правильного ответа
<question>Как обычно в эконометрике называют независимую переменную x?
<variant> Фактором
<variant> Результативным признаком
<variant> Значением регрессии
<variant> Переменной
<variant> Нет правильного ответа
<question>Какое из ниже перечисленных уравнений является уравнением парной линейной регрессии.
<variant> у = а+bх
<variant> у = а+bх+сх2
<variant> у = а+b1х1+b2х2
<variant> у = а+b/х
<variant> у = ахb
<question>Вывод параметров а, в в уравнении парной линейной регрессии осуществляется:
<variant> методом наименьших квадратов
<variant> методом Гаусса
<variant> методом определителей
<variant> методом Виета
<variant> метод Жордана
<question>Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам:
<variant> у = а+bх+сх2
<variant> у = а+bх
<variant> у = а+b1х1+b2х2
<variant> у = а+b/х
<variant> у = ахb
<question>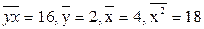
. Найти параметр b:
<variant> 4;
<variant> 5;
<variant> 0,7;
<variant> 16;
<variant> 12
<question>Регрессии, нелинейные по оцениваемым параметрам:
<variant> у = ахb
<variant> у = а+bх+сх2
<variant> у = а+b1х1+b2х2
<variant> у = а+b/х
<variant> у = а+bх
<question>Формула коэффициента корреляции для парной линейной регрессии:
<variant> r =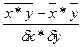 
<variant> r =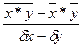 
<variant> r =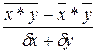 
<variant> r =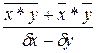 
<variant> r =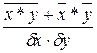 
<question>Как называется данный вид регресии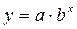 
<variant> показательная
<variant> экспоненциальная
<variant> степенная
<variant> линейная
<variant> гиперболическая
<question>Как называется данный вид регресии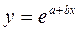 
<variant> экспоненциальная
<variant> гиперболическая
<variant> степенная
<variant> линейная
<variant> показательная
<question>Как называется данный вид регресии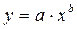 
<variant> степенная
<variant> показательная
<variant> экспоненциальная
<variant> линейная
<variant> гиперболическая
<question>Величина F критерия Фишера—это число равное отношению дисперсий
<variant> факторной к остаточной
<variant> общей к остаточной
<variant> факторной к общей
<variant> остаточной к общей
<variant> общей к общей
<question>Как называется данный вид регрессии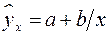 
:
<variant> равносторонняя гипербола
<variant> показательная
<variant> степенная
<variant> параболическая
<variant> экспоненциальная
<question>Как называется данный вид регрессии y=a+b*x
<variant> линейная
<variant> показательная
<variant> экспоненциальная
<variant> параболическая
<variant> гиперболическая
<question>Как называется данный вид регрессии y=a+b*lnX
<variant> полулогарифмическая функция
<variant> показательная
<variant> линейная
<variant> парабалическая
<variant> экспоненциальная
<question>Дано уравнение ŷх=4+2,1*(1/х), и среднее значение х равно 3. Найдите коэффициент эластичности для данной функции.
<variant> -0,15
<variant> 5,6
<variant> 0,7
<variant> 2,5
<variant> 0,078
<question>Дисперсия случайной величины равна 169. Определить среднеквадратическое отклонение
<variant> 13
<variant> 11
<variant> 14
<variant> 12
<variant> 15
<question>Дано уравнение ŷх=9+2,1х, и среднее значение х равно 2. Найти коэффициент эластичности для данной функции?
<variant> 0,32
<variant> 2,5
<variant> 0,7
<variant> 3,85
<variant> 9
<question>Укажите последовательность прохождения этапов эконометрического исследования:
1.спецификация модели
2. оценка параметров регрессии
3. интерпретация результатов
4. постановка проблемы
5. получения данных, анализ их качества
<variant> 4-5-1-2-3
<variant> 2-3-5-1-4
<variant> 3-5-2-4-1
<variant> 3-2-5-1-4
<variant> 1-2-3-4-5
<question>Моделирование это….
<variant> Процесс изучения, построения или применения
<variant> Новое направление в модельном бизнесе
<variant> Процесс превращения одной переменной в другую
<variant> Консервативный метод изучения математики
<variant> Нет правильного ответа
<question>Наука изучающая конкретные количественные взаимосвязи экономических объектов и процессов с помощью математических и статистических методов и моделей называется:
<variant> эконометрика
<variant> математика
<variant> экономика
<variant> теория вероятностей
<variant> статистика
<question>Аддитивная модель содержит компоненты в виде …
<variant> слагаемых
<variant> комбинации слагаемых и сомножителей
<variant> отношений
<variant> сомножителей
<variant> Нет правильного ответа
<question>Определить формулу взаимосвязи F критерия Фишера с коэффициентом корреляции
<variant> f=(r2/1-r2)*(n-2)
<variant> f=(r2/1-r2)/(n-2)
<variant> f=(r2/1-r2)+(n-2)
<variant> f=(r2/1-r2)
<variant> f=(r2/1-r2)
<question>С помощью чего оценивается значимость уравнения регрессии в целом и отдельных его параметров:
<variant> с помощью F-критерия Фишера
<variant> с помощью регрессионной статистики
<variant> нелинейных регрессий
<variant> равносторонней гиперболы
<variant> трендовых моделей
<question>По какой формуле рассчитывается коэффициент эластичности:
<variant> Э=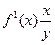 
<variant> Э=у*х/у
<variant> Э=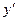 
* у/х
<variant> Э=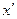 
*x/y
<variant> Э= x*y
<question>Найдите коэффициент b линейной корреляции, если σу=30, σх=6, rху=0,5
<variant> 2,5
<variant> 5,6
<variant> 0,7
<variant> 3,85
<variant> 0,078
<question>Зная коэффициент детерминации, найдите коэффициент линейной корреляции, если r2ху=0,49?
<variant> 0,7
<variant> 5,6
<variant> 2,5
<variant> 3,85
<variant> 0,078
<question>Зная коэффициент линейной корреляции найдите коэффициент детерминации если rху=0,15?
<variant> 0,0225
<variant> 5,6
<variant> 2,5
<variant> 3,85
<variant> 0,078
<question>Как называется процесс построения, изучения и пременения моделей:
<variant> моделирования
<variant> временной ряд
<variant> регрессия
<variant> корреляция
<variant> гипотеза
<question>Определите коэффициент детерминации, если b = 0,14, σу=30 σх =60.
<variant> 0,0784
<variant> 2,5
<variant> 5,006
<variant> 784
<variant> 3,85
<question>Коэффициент корреляции парной линейной регрессии находится в границах:
<variant> -1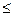 
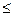r 1
<variant> r<=-1
<variant> r>0
<variant> r >= 1
<variant> r=1
<question>Непосредственному расчету F критерий Фишера предшествует анализ:
<variant> дисперсии
<variant> регрессии
<variant> корреляции
<variant> детерминации
<variant> аппроксимации
<question>Рассчитайте линейный коэффициент парной корреляции, если b = 0,14, σу=30 σх =60.
<variant> 0,28
<variant> 2,5
<variant> 5,6
<variant> 7
<variant> 2,4
<question>Коэффициент, характеризующий степень линейной функциональной зависимости между случайными величинами х и у:
<variant> коэффициент корреляции
<variant> коэффициент эластичности
<variant> коэффициент ковариации
<variant> средняя ошибка аппроксимации
<variant> коэффициент детерминации
<question>Если коэффициент корреляции равен 0 ,то случайные величины х и у:
<variant> линейно независимы
<variant> коэффициент корреляции не может быть равен 0
<variant> линейно зависимы
<variant> криволинейно зависимы
<variant> обратно зависимы
<question>Если коэфициент кореляции равен +1, то случайые величины х и у:
<variant> линейно зависимы
<variant> линейно независимы
<variant> коэфициент коррляции не может быть равен 1
<variant> криволинейно зависимы
<variant> обратно зависимы
<question>Если коэффициент корреляции равен –1, то между случайными величинами х и у:
<variant> обратная линейная зависимость
<variant> линейная независимость
<variant> линейная зависимость
<variant> криволинейная зависимость
<variant> коэффициент корреляции не может быть равен -1
<question>Чему равен индекс корреляции, если σ2ост=30 σ2у =60.
<variant> 0,71
<variant> 5,6
<variant> 2
<variant> 2,1
<variant> 30
<question>Уровень временного ряда (yt) может состоять из компонент: T - тренд, S - сезонные колебания, Е - случайная величина. Тогда аддитивная модель временного ряда может быть представлена в виде
<variant> yt = T + S + Е
<variant> yt = T·S·ε
<variant> yt = T·ε
<variant> yt = (T + S)·Е
<variant> Нет правильного ответа
<question>Средняя величина признака в совокупности равна 12, а средний квадрат индивидуальных значений этого признака равен 149. Определить среднеквадратическое отклонение?
<variant> 5
<variant> 7
<variant> 25
<variant> 10
<variant> 9
<question>Средняя величина признака в совокупности равна 10, а среднеквадратическое отклонение равно 5. Определить средний квадрат индивидуального значения этого признака?
<variant> 125
<variant> 135
<variant> 140
<variant> 116
<variant> 100
<variant> Оцените тесноту связи парной корреляции rху для линейной регрессии если
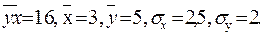
<variant> 1/5
<variant> 6
<variant> 3
<variant> 0,3
<variant> 2,4
<question>Найдите значение b в уравнении линейной регрессии ,если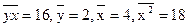 
<variant> 4
<variant> 5
<variant> 0,7
<variant> 16
<variant> 12
<question>Зная значения,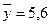 
, b =2,5 и 
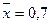, вычислите параметр а для линейной парной регрессии.
<variant> 3,85
<variant> 5,6
<variant> 0,7
<variant> 2,5
<variant> 2,4
<question>Найти коэффициент корреляции, если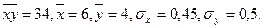 
<variant> 44,4
<variant> 0
<variant> 1
<variant> –44,4
<variant> –1
<question>Найдите ожидаемое значение себестоимости у при выпуске продукции х=5,5 тыс. шт., а=2,12, b=0,11
<variant> 2,725 тыс. тг.
<variant> 1,5 тыс. тг.
<variant> 1,515 тыс. тг.
<variant> 5,12 тыс. тг.
<variant> 0,35 тыс. тг.
<question>Найти среднюю урожайность пшеницы с 1 га за три года: 60ц, 49ц, 41ц.
<variant> 50
<variant> 41
<variant> 49
<variant> 55
<variant> Нет правильного ответа
<question>Если между факторами регрессии не существует линейной зависимости, то определитель матрицы парных коэффициентов корреляции равен
<variant> 1
<variant> -1
<variant> 0
<variant> 0,5
<variant> –0,5
<question>Дано уравнение зависимости суточной переработки сахарной свеклы от стоимости основных производственных фондов y=4,64+2,12x. Спрогнозируйте суточную переработку сахарной свеклы, если стоимость основных производственных фондов составила 2,9 тыс. ед.
<variant> 10,788
<variant> 4,988
<variant> -10,788
<variant> 5,5
<variant> -4,988
<question>Найти параметр а для линейной регрессии, если 
<variant> 2,89
<variant> 2
<variant> 0.68
<variant> 0
<variant> 1
<question>По временному тренду ŷ = 4,5 + 1,5t найти прогнозное значение в 2004г., если 2001г. соответствует t = 1, 2002г. соответствует t = 2 и т.д.
<variant> 10,5
<variant> 4,5
<variant> 6
<variant> 12
<variant> Нет правильного ответа
<question>Модель считается адекватной, если средняя ошибка аппроксимации не превышает (в %)
<variant> нет правильного ответа
<variant> 45
<variant> 30
<variant> 25
<variant> 20
<question>Под автокорреляцией уровней временного ряда подразумевается
<variant> корреляционная зависимость между последовательными уровнями временного ряда.
<variant> корреляционно-функциональная зависимость между последовательными уровнями ряда.
<variant> функциональная зависимость между двумя временными рядами.
<variant> функциональная зависимость между последовательными уровнями временого ряда.
<variant> Все ответы верны
<question>Найти параметр вдля линейной парной регрессии, если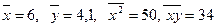 
<variant> 0,65
<variant> 0,074
<variant> 3,56
<variant> 34
<variant> 50
<question>t-критерий Стьюдента применяется:
<variant> для оценки статистической значимости коэффициентов регрессии и корреляции
<variant> для оценки тесноты связи изучаемых явлений
<variant> для расчета средних отклонений расчетных значений от фактических
<variant> для оценки качества уравнения регрессии
<variant> нет правильного ответа
<question>Если наиболее высоким оказался коэффициент автокорреляции первого порядка, то исследуемый ряд содержит
<variant> тенденцию
<variant> циклические колебания
<variant> сильную нелинейную тенденцию
<variant> сезонную компоненту
<variant> Нет правильного ответа
<question>МНК используется для оценивания …
<variant> параметров линейной регрессии.
<variant> коэффициента детерминации.
<variant> средней ошибки аппроксимации
<variant> коэффициента корреляции.
<variant> Все ответы верны
<question>Качество модели из относительных отклонений по каждому наблюдению оценивает:
<variant> средняя ошибка аппроксимации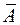 
<variant>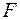 
-критерий Фишера
<variant> коэффициент детерминации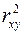 
<variant> коэффициент корреляции
<variant> дисперсия
<question>Для оценки статистической значимости коэффициентов регрессии рассчитывают:
<variant>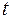 
-критерий Стьюдента
<variant> 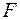-критерий Фишера
<variant> коэффициент детерминации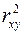
<variant> коэффициент корреляции
<variant> дисперсию
<question>Суть коэффициента детерминации 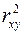состоит в следующем:
<variant> характеризует долю дисперсии результативного признака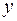 
, объясняемую регрессией, в общей дисперсии результативного признака
<variant> оценивает качество модели из относительных отклонений по каждому наблюдению
<variant> характеризует долю дисперсии 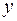, вызванную влиянием не учтенных в модели факторов
<variant> характеризует долю дисперсии x
<variant> нет правильного ответа
<question>Если коэффициент эластичности Эx = 2, то это означает, что при увеличении факторного признака на 1% результирующий признак
<variant> увеличивается на 2%
<variant> уменьшается на 2%
<variant> увеличивается на 200%
<variant> уменьшается на 200%
<variant> нет правильного ответа
<question>Зная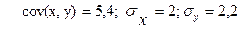 
определите rух.
<variant> 1,23
<variant> 5,4
<variant> 0,325
<variant> 0,56
<variant> 0
<question>Если фактическое значение 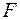-критерия больше табличного, то
<variant> признается статистическая значимость уравнения в целом
<variant> характеризует долю дисперсии x
<variant> циклические колебания
<variant> сильную нелинейную тенденцию
<variant> сезонную компоненту
<question>Линейная двухфакторная модель содержит число коэффициентов, равное
<variant> 2
<variant> 1
<variant> 3
<variant> 4
<variant> нет правильного ответа
<question>Найдите параметр адля у = а + bх, если 
.
<variant> 1,2
<variant> 4,6
<variant> 0,325
<variant> 0,56
<variant> 2,1
<question>Дана линейная регрессия , в которой коэффициент регрессии b=-0,11; 
найти значения параметра а.
<variant> 2,12
<variant> 48
<variant> 2,5
<variant> 0,56
<variant> 0
<question>Коэффициент корреляции определяется формулой
<variant> 
<variant> 
<variant> 
<variant> 
<variant> нет правильного ответа
<question>Чему равен коэффициент множественной детерминации, если 
.
<variant> 0,81
<variant> 5,4
<variant> 0,325
<variant> 0,56
<variant> 0
<question>Чему равен коэффициент множественной детерминации, если 
.
<variant> 0,64
<variant> -0.11
<variant> 0,325
<variant> 0,56
<variant> 0
<question>Первым этапом регрессионного анализа является
<variant> определение типа функции
<variant> определение и проверка коэффициентов регрессии
<variant> расчет значений функций для отдельных значений аргумента
<variant> исследование рассеивания по отклонениям расчетных значений от эмпирических данных
<variant> нет правильного ответа
<question>Если коэффициент корреляции равен 1, то связь
<variant> функциональная
<variant> отсутствует
<variant> прямая
<variant> обратная
<variant> нет правильного ответа
<question>С помощью корреляционной таблицы определяются
<variant> наличие или отсутствие парной корреляционной связи
<variant> коэффициенты парной корреляции
<variant> коэффициенты множественной корреляции
<variant> коэффициенты уравнения регрессии
<variant> нет правильного ответа
<question>Частная корреляция - это зависимость
<variant> между результативным и одним факторным признаком при фиксированном значении других факторных признаков
<variant> результативного и трех признаков, включенных в исследование
<variant> между результативным и факторным признаком
<variant> результативного и двух признаков, включенных в исследование
<variant> нет правильного ответа
<question>Коэффициент регрессии a1, показывает
<variant> на сколько в среднем изменится значение результативного признака при изменении факторного признака на единицу собственного значения
<variant> значение неучтенных факторов
<variant> в случае а0 = 0 отсутствие неучтенных факторов
<variant> во сколько раз изменится значение результативного признака при изменении факторного признака на единицу собственного значения
<variant> нет правильного ответа
<question>Коэффициент множественной корреляции Rопределяется в интервале
<variant> 0≤ r ≤1
<variant> -1≤ R ≤0
<variant> -1≤ R ≤ 1
<variant> 
<variant> нет правильного ответа
<question>Уравнение множественной регрессии в стандартизованном масштабе:
<variant> 
<variant>
<variant> yt = (T + S)·Е
<variant> yt = T + S + Е
<variant> нет правильного ответа
<question>Индекс множественной корреляции:
<variant> 
<variant> 
<variant> yt = (T + S)·Е
<variant>
<variant> нет правильного ответа
<question>Определите индекс множественной корреляции, если известны 
, 
.
<variant> 0,71;
<variant> 0,2;
<variant> 0,325;
<variant> 0,56;
<variant> 0.
<question>Временной ряд - это
<variant> совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени;
<variant> между результативным и факторным признаком;
<variant> результативного и двух признаков, включенных в исследование;
<variant> между результативным и одним факторным признаком при фиксированном значении других факторных признаков;
<variant> нет правильного ответа
<question>Случайная ошибка 
коэффициента регрессии по параметру b определяется:
<variant> 
<variant>
<variant> yt = (T + S)·Е
<variant>
<variant> нет правильного ответа
<question>Остаточная дисперсия на одну степень свободы:
<variant> 
–
<variant>
<variant>
<variant>
<variant> нет правильного ответа
<question>Остаточная дисперсия:
<variant> 
<variant>
<variant> 
<variant>
<variant> нет правильного ответа
<question> 
_?
<variant> индекс детерминации
<variant> число наблюдений
<variant> число параметров при переменной
<variant> остаточная дисперсия на одну степень свободы
<variant> нет правильного ответа
<question> 
- это
<variant> cтандартизированные переменные;
<variant> число параметров при переменной
<variant> остаточная дисперсия на одну степень свободы
<variant> индекс детерминации
<variant> нет правильного ответа
<question>Формула для расчета коэффициента автокорреляции:
<variant> 
<variant>
<variant>
<variant>
<variant> нет правильного ответа
<question>Коэффициент автокорреляции второго порядка:
<variant> 
<variant>
<variant>
<variant>
<variant> нет правильного ответа
<question>Уравнение линейного тренда:
<variant> 
;
<variant>
<variant>
<variant>
<variant> нет правильного ответа
<question> 
– ?
<variant> теоретическое значение результативного признака;
<variant> фактическое значение результативного признака;
<variant> случайная величина, характеризующая отклонения реального значения результативного признака от теоретического;
<variant> уравнение линейной регрессии;
<variant> нет правильного ответа
<question>
- ?
<variant> парабола второй степени
<variant> фактическое значение результативного признака;
<variant> случайная величина, характеризующая отклонения реального значения результативного признака от теоретического;
<variant> уравнение линейной регрессии;
<variant> нет правильного ответа
<question>Параметр 
называется:
<variant> коэффициентом регрессии;
<variant> уравнение линейной регрессии;
<variant> парабола второй степени;
<variant> фактическое значение результативного признака;
<variant> нет правильного ответа
<question> -?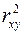
<variant> коэффициент детерминации;
<variant> коэффициента корреляции;
<variant> уравнение линейной регрессии;
<variant> парабола второй степени;
<variant> нет правильного ответа
<question> -?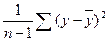
<variant> Общая сумма квадратов отклонений;
<variant> Факторная сумма квадратов отклонений;
<variant> Остаточная сумма квадратов отклонений;
<variant> Среднее значение
<variant> нет правильного ответа
<question> -?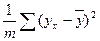
<variant> Факторная сумма квадратов отклонений;
<variant> Общая сумма квадратов отклонений;
<variant> Остаточная сумма квадратов отклонений;
<variant> Среднее значение
<variant> нет правильного ответа
<question> -?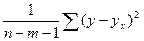
<variant> Остаточная сумма квадратов отклонений;
<variant> Общая сумма квадратов отклонений;
<variant> Факторная сумма квадратов отклонений;
<variant> Среднее значение
<variant> нет правильного ответа
<question> 
Найти параметры а и b?
<variant> -0,035; 8,14
<variant> 1.2 ; 4.6
<variant> -0,035 ; 81,4
<variant> 0, 035 ; -8, 14
<variant> 8,14 ; -0,035
<question>y 
(x) 
- ?
<variant> коэффициент эластичности;
<variant> коэффициент детерминации;
<variant> коэффициента корреляции;
<variant> уравнение линейной регрессии;
<variant> нет правильного ответа
<question> 
Найти коэффициент корреляции:
<variant> 0,96
<variant> 0,91
<variant> 0,45
<variant> –0,96
<variant> –0,54
<question> 
Найти параметры а и b:
<variant> a=2, b= 
<variant> a=1, b=2
<variant> a=3, b= 
<variant> a= 
b=1
<variant> a= 
, b= .
<question> 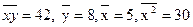найти параметр в:
<variant> 0,4.
<variant> 48;
<variant> 30
<variant> 0
<variant> 0.28
<question> 
для линейной регрессии найти rху :
<variant> 0,2;
<variant> 5;
<variant> 6;
<variant> 3;
<variant> 2,4.
<question>f / (х1)= 0,5, 
найти коэффициент эластичности?
<variant> 2,5;
<variant> 5,6;
<variant> 0,7;
<variant> 3,85;
<variant> 2,4.
<question>Найти среднее арифметическое чисел 5,6,10:
<variant> 7
<variant> 5
<variant> 4
<variant> 8
<variant> 6
<question>Имея следующие данные, найти параметр b:
гху = 0,85, σу = 36, σх = 49.
<variant> 0,624
<variant> 0,614
<variant> 0,5
<variant> -0,624
<variant> -0,614
<question>Имея следующие данные, найти параметр b:
гху = 0,994, σу = 0,935, σх = 5,53.
<variant> 0,168
<variant> 0,990
<variant> 0,980
<variant> -0,168
<variant> -0,980
<question>По следующим данным рассчитайте коэффициент корреляции:
Σх = 71,6, Σу =18,7, Σxy =208,71, Σx2=885,24, Σy2=50,83, n =8
<variant> 0,988
<variant> 0,399
<variant> 0,587
<variant> -0,994
<variant> -0,288
<question>По следующим данным рассчитайте индекс корреляции:
σост2 = 0,0711, σу2= 0,874
<variant> 0,959
<variant> 0,955
<variant> 0,956
<variant> -0,957
<variant> -0,954
<question>По следующим данным рассчитайте индекс корреляции:
σост2 = 28,27, σу2= 32,92
<variant> 0,3755
<variant> 0,3750
<variant> 0,3730
<variant> -0,3758
<variant> -0,3750