Графическая технология решения задач на пересечение прямой линии с поверхностью
( рис.16.23 )
Решение задачи №8
Предварительные замечания.
Так как, согласно условию, во вза-имодействие вступают прямая линия и поверхность, то особенности графичес-кого построения общих для них точек определяются как их положением в пространстве, так и видом пересекае-мых поверхностей.
Так как многогранные поверхности являются прототипами кривых, то в ус-ловие задачи №8 введем поверхности цилиндрические, конические общего положения. и вращения с вертикаль-ной осью.
Задача №8.1.Построить двухкар-тинный комплексный чертёж точек встречи прямой линии а с поверхнос-тью цилиндра Ф;
Задача №8.2 Построить двухкар-тинный комплексный чертёж точек встречи прямой линии а с поверхнос-тью конуса S;
Задача №8.3. Построить двухкар-тинный комплексный чертёж точек встречи прямой а с поверхностью вращения W с вертикальной осью.
Решение задачи №8.1
(рис.16.23, п.п.1.1 -1.5)
Согласно условию этой задачи, во взаимодействие вступают прямые ли-нии частного и общего положений с прямолинейчатыми цилиндрическими поверхностями общего положения.
Если прямые занимают проециру-
ющее положение, то их вырожденные
|
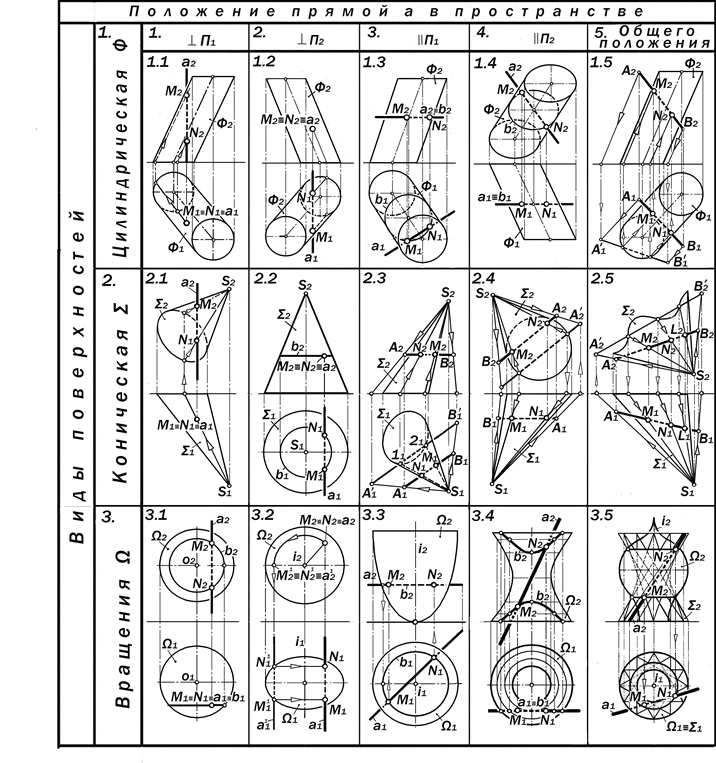
Рис. 16.23.Варианты решения позиционных задач на пересечение прямой линии с кривыми поверхностями
в точки проекции, в силу и х собирате-
льного свойства, содержат в себе одно-
именные проекции искомых точек их встречи с заданными поверхностями.
Недостающие проекции этих точек сле- дует строить моделируя их принадлеж-
ность к заданным поверхностям ( п.п.
1.1,1.2).
2. Если прямые занимают положе-ния линий уровня, параллельных осно-ваниям поверхностей, то их следует за-ключать в плоскости уровня, рассекаю-
|
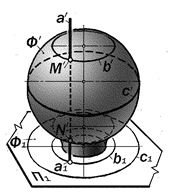
Рис. 16.24. Геометрическая модель
построения точек встречи проецирующей прямой с поверхностью вращения

|
Рис. 16.25.Геометрическая модель построения точки встречи горизонтальной прямой а
с поверхностью вращения

|
Рис.16.26.Геометрическая модель построения точек встречи прямой общего положения с поверхностью
вращения
щие эти поверхности по линиям, кон-
груэнтным их основаниям. Эти линии пересекут заданные прямые в искомых точках их встречи с заданными поверх-ностями ( п.п.1.3,1.4 ).
3. Если прямая и поверхность зани-мают общее положение, то эту прямую следует заключить в такую плоскость общего положения, которая пересечет эту поверхность по двум образующим.
Для этого необходимо (рис.16.21):
3.1. Концы отрезка А и В прямой а спроецировать на плоскость любого ос-нования данной поверхности по напра-влению её образующих и построить соответствующие следы А¢ и В¢ прое-цирующих прямых;
3.2. Соединив А¢ с В¢ прямой а¢, отметить точки М1¢ и N1¢ её пересече-
ния с основанием поверхности;
3.3. Образующие l поверхности Ф, выходящие из М1¢ и N1¢, пересекают прямую а в искомых точках М и N её встречи с поверхностью Ф.
Графическое моделирование этого геометрического алгоритма самоочеви-дно.
Решение задачи №8.2.
(рис. 16.23, п.п.2.1- 2.5)
Согласно условию этой задачи, во взаимодействие вступают прямые част-ного и общего положения с прямоли-
нейчатыми коническими поверхностя-ми, оси которых занимают в простран-стве общее положение.
1. Если прямые занимают проеци-рующие положения, то их вырожден-ные проекции, в силу собирательного свойства, содержат в себе соответству-ющие проекции искомых точек встречи этих прямых с заданными поверхностя-ми. Недостающие проекции этих точек строятся на основе графического моде-лирования их принадлежности к задан-ной поверхности, т.е., к тем её образу-ющим, которые проходят через эти точ-ки ( п.п.2.1, 2.2 ).
2.Если прямые в пространстве за-нимают положения линий уровня или общее положение, то каждая из них, в паре с вершиной S заданной поверх-ности S определяет вспомогательную плоскость s, пересекающую эту повер-хность по двум образующим, которые, в свою очередь, пересекают прямую а в
искомых точках М и N её встречи с по-верхностью S ( п.п.2.3 – 2.5). В данном случае плоскость основания поверхнос-ти является вспомогательной секущей плоскостью проецирующего положения, пересекающей поверхность конуса по его основанию m, а секущую плоскость s - по прямой А¢ В¢, которая, в свою очередь, пресекает это основание в то-чках 1 и 2 начала образующих 1S и 2S, дающих в пересечении с а искомые то-чки М и N ( рис.16.23).
Графическое моделирование этой геометрической ситуации самоочевид-но.
Решение задачи №8.3
(рис.16.23, п.п.3.1 – 3.5)
Согласно условию этой задачи, во взаимодействие вступают прямые част-ного и общего положения с криволиней-чатыми поверхностями вращения с вертикальной осью. Линейный каркас этих поверхностей состоит из конгру-энтных криволинейных меридианов различной формы и подобных друг дру-гу параллелей-окружностей, плоскости которых в данном случае горизонта-льны. Будучи наиболее простыми на поверхности вращения, они использу-ются для рационального решения пос-тавленной задачи.
1.Если прямые занимают проеци-рующие положения, то их вырожден-ные в точки проекции содержат в себе соответствующие проекции искомых то-чек встречи этих прямых с заданными поверхностями. Недостающие проек-ции этих точек строятся на основе гра-фического моделирования отношения их принадлежности в заданной поверх-ности, т.е., к тем её параллелям, кото-рые проходят через эти точки ( п.п.3.1,
3.2) (рис.16.24).
2.Если прямая а горизонтальна, то плоскость уровня s, проходящая через неё, пересечет поверхность вращения W по её параллели-окружности b, с ко-торой прямая а пересечется в искомых точкам М и N встречи этой с заданной поверхностью ( п.3.3) (рис.16.25).
3.Еслипрямая а фронтальна или общего положения, то её следует за-ключить в поверхность однополостного гиперболоида вращения, соосную с за-
данной поверхностью и пересекающую

|
Рис. 16.27. Геометрическая модель построения линии пересечения двух многогранных поверхностей
|
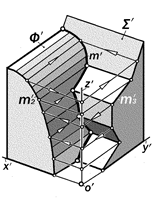
Рис.16.28. Геометрическая модель построения линии пересечения многогранной и кривой поверхностей
|
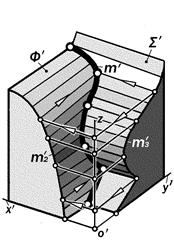
Рис.16.29. Геометрическая модель построения линии пересечения двух кривых поверхностей
её по параллелям-окружностям, кото-
рые, в свою очередь, пересекают дан-ную прямую а в искомых точках её встречи с данной поверхностью W ( п.п. 3.4, 3.5) ( рис. 16.26).