Принцип сообщающихся сосудов и его использование.

Практическое применение основного уравнения гидростатики

 

Основное уравнение гидростатики, выражаемое часто в виде закона Паскаля, имеет ряд важных практических приложений.

Пусть два открытых сообщающихся сосуда заполнены жидкостью плотностью ρ(рисунок 3 а).

 

 

Выберем произвольную плоскость сравнения 0-0 и некоторую точку А внутри жидкости, лежащую в этой плоскости. Если считать точку а принадлежащей левому сосуду, то, согласно закону Паскаля давление в этой точке:

 

 

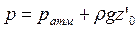
Если же считать точку А принадлежащей правому сосуду, то давление в ней:

 

 

где z’ и z’’ = 0, так как плоскость 0-0 проходит через точку А.

 

При равновесии для каждой точки давление одинаково в любом направлении (в противном случае происходило бы перемещение жидкости).

Следовательно:

 

,

Или ,

 

Аналогичный вывод может быть сделан для двух закрытых сообщающихся сосудов, в которых давления над свободной поверхностью жидкости одинаковы.

Таким образом, в открытых или закрытых находящихся под одинаковым давлением сообщающихся сосудах, заполненных однородной жидкостью, уровни ее располагаются на одной высоте независимо от формы и поперечного сечения сосудов.

Если сообщающиеся сосуды заполнены двумя несмешивающимися жидкостями, имеющими плотности ρ’ (левый сосуд) и ρ” (правый сосуд), то при проведении плоскости сравнения 0-0 через границу раздела жидкостей (рисунок 3 б) аналогично предыдущему получим:

 

 

Или ,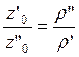

 

Отсюда следует, что в сообщающихся сосудах высоты уровней разнородных жидкостей над поверхностью их раздела обратно пропорциональны плотностям этих жидкостей.

Если сосуды заполнены одной жидкостью плотностью ρ, но давление над уровнем жидкости в них неодинаковы и равны p’ (левый сосуд) и p” (правый сосуд), то:

 

,

 

Откуда разность уровней жидкости в сосудах:

 

,

 

Последнее уравнение применяется при измерении давлений или разностей давлений между различными точками с помощью дифференциальных U – образных монометров.

Условия равновесия жидкостей в сообщающихся сосудах используют также для определения высоты гидравлического затвора в различных аппаратах.