Тема № 9. Оценка тесноты связи

 

108.Коэффициент корреляции может принимать значения в интервале…

1. от -2 до 2

2. от 0 до 100

3. от -1 до 1

4. от 0 до 4

5.от -1 до 0

 

109.Положение на плоскости каждой точки корреляционного поля определяется значениями …

1. коэффициентов детерминации и корреляции

2. величинами остатков в предыдущем наблюдении и последующем

3. факторного и результативного признаков для конкретного наблюдения

4. коэффициентов автокорреляции первого и второго порядков

5. коэффициентов множественной корреляции

 

110.Коэффициент парной линейной корреляции между признаками Y и X равен 0,9. Следовательно, доля дисперсии результативного признака Y, не объяснённая линейной парной регрессией Y по фактору X, будет равна …

1. 0,1%

2. 10%

3. 19%

4. 90%

5. 0,9

 

111.Частный коэффициент корреляции это означает, что…

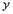1. и независимы, когда величины и фиксированы

2. и линейно зависимы, когда величины 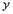и фиксированы

3. 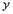и линейно зависимы, когда величины и фиксированы

4. 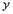и независимы, когда величины и фиксированы

5. ничего не означает

 

112.Тесноту линейной связи определяет коэффициент …

1. регрессии

2. существенности

3. корреляции

4. эластичности

5. несмещенности

 

113.Коэффициент парной линейной корреляции является …

1. размерной величиной, той же размерности, что результативный признак

2. безразмерной величиной

3. размерной величиной, той же размерности, что факторный признак

4. величиной с переменной единицей измерения

5. величиной с постоянной единицей измерения

 

114.Коэффициент множественной линейной корреляции применяется для …

1. вычисления коэффициента парной линейной корреляции

2. диагностики гомоскедастичности остатков

3. определения тесноты связи между результатом и совокупностью факторов в случае множественной линейной зависимости

4. определения значимости оценок параметров регрессии

5. определения значимости факторов регрессии

 

115.Построена парная модель линейной регрессии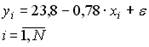

и рассчитан коэффициент парной линейной корреляции . Такие результаты невозможны, так как …

1. коэффициент регрессии и коэффициент корреляции имеют разные знаки

2. свободный член регрессии больше коэффициента корреляции

3. свободный член регрессии и коэффициент корреляции имеют одинаковые знаки

4. коэффициент регрессии по модулю меньше коэффициента корреляции

5. коэффициент регрессии и коэффициент корреляции имеют общие знаки

 

 

116.Предпосылкой применения корреляционного анализа является утверждение:

1. совокупность значений факторных и результативных признаков имеет распределение Стьюдента

2. совокупность значений факторных признаков распределена по нормальному закону, а результативного – по произвольному

3. совокупность значений результативного признака распределена по нормальному закону, а закон распределения совокупности факторных признаков – произвольный

4. совокупность значений факторных и результативных признаков распределена по нормальному закону

5. совокупность значений факторных признаков распределена по общему закону