Частотные динамические характеристики
Частотные характеристики описывают передаточные свойства элементов и систем в режиме установившихся гармонических колебаний, вызванных внешним гармоническим воздействием. Зная частотную характеристику элемента, можно определить реакцию элемента на гармоническое воздействие любой частоты, а также на сумму гармонических воздействий различной частоты. Частотные характеристики широко используются в теории и практике автоматического управления, так как реальные возмущения, действующие на автоматические системы, могут быть представлены как сумма гармонических сигналов.
1. Передаточная функция звена (W(p)).
2. Амплитудная частотная характеристика (АЧХ).
3. Фазовая частотная характеристика (ФЧХ).
4. Амплитудно-фазовая характеристика (АФХ).
5. Логарифмическая амплитудно-частотная характеристика (ЛАЧХ).
Передаточной функцией W(p) называют отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях.

Допустим динамика описывается дифференциальным управлением:
 Применим к данному уравнению прямое преобразование Лапласа:
Применим к данному уравнению прямое преобразование Лапласа:

Зависимость отношения амплитуд выходного и входного сигнала от частоты называют амплитудной частотной характеристикой (сокращенно - АЧХ) и обозначают А(w) (см. рис.а). Зависимость фазового сдвига между входным и выходным сигналами от частоты называют фазовой частотной характеристикой (ФЧХ) и обозначают j(w) (см. рис.б). Аналитические выражения А(w) и j(w) называют соответственно амплитудной и фазовой частотными функциями.

АЧХ показывает, как элемент пропускает сигналы различной частоты. Оценка пропускания производится по отношению амплитуд  в установившемся режиме. АЧХ имеет размерность, равную отношению размерности выходной величины к размерности входной. ФЧХ показывает, какое отставание или опережение выходного сигнала по фазе создает элемент при различных частотах в установившемся режиме.
в установившемся режиме. АЧХ имеет размерность, равную отношению размерности выходной величины к размерности входной. ФЧХ показывает, какое отставание или опережение выходного сигнала по фазе создает элемент при различных частотах в установившемся режиме.
Амплитудную и фазовую частотные характеристики можно объединить в одну общую – амплитудно-фазовую частотную характеристику (АФЧХ или АФХ). Амплитудно-фазовая частотная характеристикаW(jw) представляет собой функцию комплексного переменного jw, модуль которой равен А(w), а аргумент равен j(w). Каждому фиксированному значению частоты wi соответствует комплексное число W(jwi), которое на комплексной плоскости можно изобразить вектором, имеющим длину А(wi) и угол поворота j(wi) (см. рис.в). Отрицательные значения j(w), соответствующие отставанию выходного сигнала от входного, принято отсчитывать по часовой стрелке от положительного направления действительной оси.
При изменении частоты от нуля до бесконечности вектор W(jw) поворачивается вокруг начала координат, при этом одновременно увеличивается или уменьшается длина вектора. Кривая, которую при этом опишет конец вектора, называемая годографом, и есть АФХ. Каждой точке характеристики соответствует определенное значение частоты.
Проекции вектора W(jw) на действительную и мнимую оси называют соответственно действительной и мнимой частотными характеристиками и обозначают
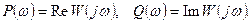
При этом, действительная частотная характеристика Р(w) – всегда четная функция частоты, а мнимая характеристика Q(w) – всегда нечетная функция.
Аналитическое выражение для АФХ конкретного элемента можно получить из его передаточной функции путем подстановки р=jw:

АФХ W(jw), как и любая комплексная величина, может быть представлена в показательной форме

где А(w) – модуль АФХ, а j(w) – угол сдвига по фазе;
алгебраической

или тригонометрической
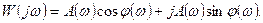
Связь между различными частотными функциями следующая:

Физический смысл замены р=jw: на вход звена мы подаем гармоническое воздействие 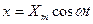 , на выходе звена -
, на выходе звена -  , тоже имеем гармонический сигнал, но с другой амплитудой и со сдвигом по фазе.
, тоже имеем гармонический сигнал, но с другой амплитудой и со сдвигом по фазе.
При практических расчетах автоматических систем удобно использовать частотные характеристики, построенные в логарифмической системе координат. Такие характеристики называют логарифмическими. Они имеют меньшую кривизну и поэтому могут быть приближенно заменены ломаными линиями, составленными из нескольких прямолинейных отрезков. Причем, эти отрезки в большинстве случаев удается построить без громоздких вычислений при помощи некоторых простых правил. Кроме того, в логарифмической системе координат легко находить характеристики различных соединений элементов, так как умножению и делению обычных характеристик соответствует сложение и вычитание ординат логарифмических характеристик.
За единицу длины по оси частот логарифмических характеристик принимают декаду. Декада – интервал частот, заключенный между произвольным значением wi и его десятикратным значением 10wi. Отрезок логарифмической оси частот, соответствующий одной декаде, равен 1.
Обычно в расчетах используют логарифмическую амплитудную частотную характеристику (ЛАЧХ)

ординаты которой измеряют в логарифмических единицах – белах (Б) или децибелах (дБ).
При построении фазовой частотной характеристики логарифмический масштаб применяют только для оси абсцисс.
На рис.г показаны ЛАЧХ L(w) (толстая линия) и соответствующая ей приближенная (асимптотическая) характеристика Lа(w) в виде прямолинейных отрезков (тонкая линия). Частоты, соответствующие точкам стыковки отрезков, называют сопрягающими и обозначают wс.