ОСНОВЫ РЕЛЯЦИОННОЙ АЛГЕБРЫ
С точки зрения внешнего представления (абстрагированияна логическом уровне) объектов реального мира модель данных — это основные понятия и способы, используемые при анализе и описании предметной области.
Среди многих попыток представить обработку данных на формальном абстрактном уровне реляционная модель, предложенная Э. Ф. Коддом, стала по существу первой работоспособной моделью данных, поскольку помимо средств описания объектов имела эффективный инструментарий преобразований этих описаний — операции реляционной алгебры.
Реляционная алгебра в том виде, в котором она была определена Э. Ф. Коддом, состоит из двух групп по четыре оператора.
1. Традиционные операции над множествами (но модифицированные с учетом того, что их операндами являются отношения, а не произвольные множества): объединение, пересечение, разность и декартово произведение.
2. Специальные реляционные операции: выборка, проекция, соединение, деление.
Рассмотрим подробнее операции реляционной алгебры.
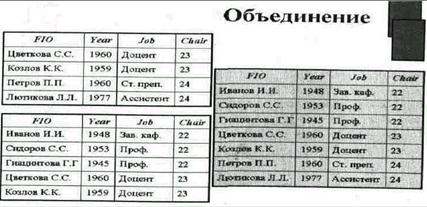
Объединение возвращает таблицу, содержащую все записи, которые принадлежат либо одной из двух заданных таблиц, либо им обоим.
Пересечение возвращает таблицу, содержащую все записи, которые принадлежат одновременно двум заданным таблицам.
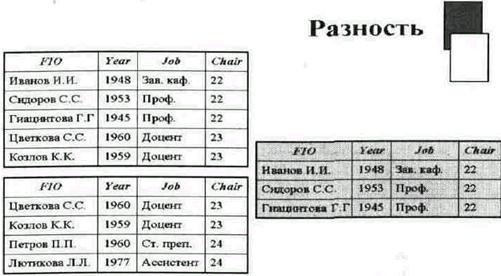
Разность возвращает таблицу, содержащую все записи, которые принадлежат первому из двух заданных таблиц и не принадлежат второй.
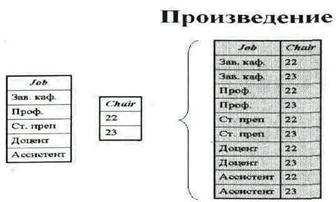
Произведение возвращает таблицу, содержащую все возможные записи, которые являются сочетанием двух записей, принадлежащих соответственно двум заданным таблицам.
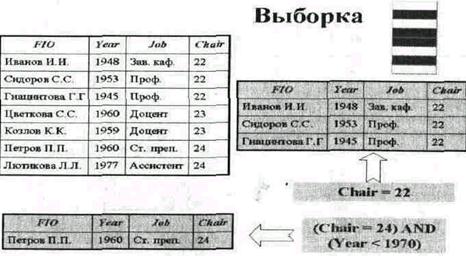
Выборка возвращает таблицу, содержащую все записи из заданной таблицы, которые удовлетворяют указанным условиям.
Проекция возвращает таблицу, содержащую все записи заданной таблицы, которые остались в этой таблицы после исключения из неё некоторых атрибутов
Соединение возвращает таблицу, содержащую все возможные записи, которые представляют собой комбинацию атрибутов двух записей, принадлежащих двум заданным таблицам, при условии, что в этих двух комбинированных записях присутствуют одинаковые значения в одном или нескольких общих для исходных таблиц атрибутах (причем эти общие значения в результирующем записи появляются один раз, а не дважды).



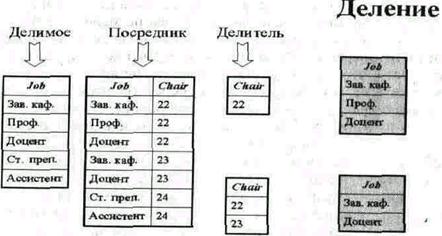
Деление для заданных двух унарных таблиц и одной бинарной возвращает таблицу, содержащую все записи из первой унарной таблицы, которые содержатся также в бинарной таблице и соответствуют всем записям во второй унарной таблице.
Результат выполнения любой операции над таблицами также является таблицей, поэтому результат одной операции может использоваться в качестве исходных данных для другой. Другими словами, можно записывать вложенные реляционные выражения, т. е. выражения, в которых операторы сами представлены реляционными выражениями, причем произвольной сложности. Эта особенность называется свойством реляционной замкнутости.