Основные теоремы электростатики в интегральной и дифференциальной форме.
1) Теорема Гаусса.
(вакуум)
(среда)
По теореме преобразования поверхностного интеграла в объемный (теореме Остроградского) имеем:
откуда следует дифференциальная форма записи теоремы Гаусса:
где ρ – объемная плотность стороннихзарядов;
.
Используя определение 
, нетрудно показать, что 
, где 
- объемная плотность связанных зарядов.
2) Теорема о циркуляции электрического поля. 
По теореме преобразования контурного интеграла в поверхностный (теореме Стокса) имеем:
,
откуда следует дифференциальная форма второй основной теоремы электростатики
где 
.
Граничные условия для электрического поля.
При переходе через границу раздела двух диэлектриков с различными диэлектрическими проницаемостями ε1 и ε2 (рис.3.12) необходимо учитывать граничные условия для полей
и
, которые непосредственно вытекают из основных интегральных теорем электростатики.
Нормальные составляющие индукции поля непрерывны
Учитывая, что 
, находим также: 
Тангенциальные составляющие электрического поля непрерывны
Поскольку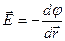 
, то 