Основы массообмена. Топливо. Основы теории горения. Возобновляемые источники энергии. Промышленные котельные установки.

Рис.14.1. Схема распределение тепла при лучистом теплообмене

Теплопередача. Тепловая изоляция. Критический диаметр тепловой изоляции. Основы расчёта теплообменных аппаратов. Конструктивные особенности теплообменников рекуперативного, регенеративного и смесительного типов.

Основные критериальные числа (Нуссельта, Рейнольдса, Прандтля, Грасгофа, Пекле). Виды уравнений подобия конвективного теплообмена. Определяющие параметры. Приложение теории подобия - моделирование. Критериальные уравнения теплоотдачи при свободном и вынужденном движении текучей среды.

Уравнение Ньютона-Рихмана. Коэффициент теплоотдачи. Свободная и вынужденная конвекция. Ламинарный и турбулентный режим течения. Дифференциальные уравнения переноса тепловой энергии, неразрывности, теплоотдачи в пограничном слое и течения вязкого теплоносителя (Навье-Стокса).

 

Уравнение Ньютона-Рихмана

Процесс теплообмена между поверхностью тела и средой описывается уравнением Ньютона-Рихмана, согласно которому, количество теплоты, передаваемая конвективным теплообменом прямо пропорционально разности температур поверхности тела (t'ст) и окружающей среды (t'ж):

Q = α·(t'ст - t'ж)·F, или q = α·(t'ст - t'ж), где: α - коэффициент теплоотдачи [Вт/(м2К)], характеризует интенсивность теплообмена между поверхностью тела и окружающей средой.

На процесс теплоотдачи влияет:

1). Природа возникновения движения жидкости вдоль поверхности стенки.

Самопроизвольное движение жидкости (газа) в поле тяжести, обусловленное разностью плотностей её горячих и холодных слоев, называют свободным движением (естественная конвекция). Движение, создаваемое вследствие разности давлений, которые создаются насосом, вентилятором и другими устройствами, называется вынужденным (вынужденная конвекция).

2). Режим движения жидкости. Упорядоченное, слоистое, спокойное, без пульсаций движение называется ламинарным. Беспорядочное, хаотическое, вихревое движение называется турбулентным.

3). Физические свойства жидкостей и газов. Большое влияние на конвективный теплообмен оказывают следующие физические параметры: коэффициент теплопроводности (λ), удельная теплоемкость (с), плотность (ρ), коэффициент температуропроводности (а = λ/cр·ρ), коэффициент динамической вязкости (μ) или кинематической вязкости (ν = μ/ρ), температурный коэффициент объемного расширения (β = 1/Т).

4). Форма (плоская, цилиндрическая), размеры и положение поверхности (горизонтальная, вертикальная).

Коэффициент теплоотдачи является функцией параметров процесса т.е.

α = f1(Х; Ф; l0; xc; yc; zc; w0; θ; λ; а; ср; ρ; ν; β) ,

где: Х – характер движения среды (свободная, вынужденная);

Ф – форма поверхности;

l0– характерный размер поверхности (длина, высота, диаметр и т.д.);

xc; yc; zc – координаты; w0 – скорость среды (жидкость, газ); θ = (t'ст - t'ж) – температурный напор; λ – коэффициент теплопроводности среды;

а – коэффициент температуропроводности среды; ср –изобарная удельная теплоемкость среды; ρ –плотность среды; ν – коэффициент кинематической вязкости среды; β – температурный коэффициент объемного расширения среды.

Сложность в определении коэффициента теплоотдачи решают применением экспериментальный или численных методов исследования.

Достоинством экспериментального метода является: достоверность получаемых результатов; основное внимание можно сосредоточить на изучении величин, представляющих наибольший практический интерес.

Основным недостатком этого метода является, что результаты данного эксперимента не могут быть использованы, применительно к другому явлению, которое в деталях отличается от изученного. Поэтому выводы, сделанные на основании анализа результата проведенного экспериментального исследования, не допускают распространения их на другие явления. Следовательно, при экспериментальном методе исследования каждый конкретный случай должен служить самостоятельным объектом изучения. Применение численных методов исследования позволяют на базе построения исследования математической модели процесса описать многообразие режимов теплоотдачи при различных начальных и граничных условиях задачи.

Конвективный теплообмен при движении жидкости под действием неоднородного поля массовых сил (гравитационного, магнитного, электрического) называется свободной конвекцией.

Конвективный теплообмен при движении жидкости под действием внешних сил, приложенных на границах системы или однородного поля массовых сил приложенных к жидкости внутри системы или за счет кинетической энергии сообщенной жидкости вне системы – вынужденная конвекция.

Порядок величин коэффициента теплоотдачи α [Вт/(м2К)], для различных условий конвективного теплообмена приведен ниже:

Свободная гравитационная конвекция в газах 5 – 30
Вынужденная конвекция газов 10 – 500
Свободная конвекция воды 102 – 103
Вынужденная конвекция воды 500 - 2•104
Жидкие металлы 102 - 3•104
Кипение воды 2•103 - 4•104
Пленочная конденсация водяных паров 4•103 – 1,5•104
Капельная конденсация водяных паров 4•104 – 1,2•105

В зависимости от рода жидкости, скорости ее движения и характера стенок, ограничивающих поток, различают два основных режима движения: ламинарный и турбулентный. Ламинарным (а) называют упорядоченное движение, когда отдельные слои скользят друг по другу, не перемешиваясь.

Ламинарный режим движения можно наблюдать чаще у вязких жидкостей, таких как нефть, масла и т. п.

Турбулентным (б) называют режим, при котором наблюдается беспорядочное движение, когда частицы жидкости движутся по сложным траекториям и слои жидкости постоянно перемешиваются друг с другом.

Конвективный теплообмен усиливается хаотическими движениями частиц жидкости в турбулентном потоке. Поэтому при турбулентном режиме течения теплообмен происходит интенсивнее чем при ламинарном.

Дифференциальные уравнения переноса тепловой энергии, неразрывности, теплоотдачи течения вязкого теплоносителя (Навье-Стокса).

Уравнение энергии

Первое начало термодинамики для элементарного объема движущейся среды можно записать в виде: , где - количество теплоты единицы объема в единицу времени, ; - работа, совершаемая внешними силами над единицей объема среды в единицу времени, ; - время, с; - плотность среды, ; - удельная внутренняя энергия, ; - скорость движения среды, .

Уравнение теплового баланса выделенного элемента конечного объема , ограниченно поверхностью запишется в виде: ,

здесь - количество теплоты единицы объема, ; - поток теплоты, проходящий через поверхность, ; - интенсивность внутренних источников теплоты (таких, как объемные химические реакции, радиоактивный распад, работа трения и т.д.), . Используя положение Гаусса-Остроградского, определяющее переход от поверхностного интеграла к объемному интегралу можно записать: , - дивергенция (расхождение) теплового потока в окрестности выделенного элементарного объема. Подставляя значение имеем: .

Принимая для вектора теплового потока гипотезу Фурье, имеем: , где - декартовые координаты.

Если коэффициент теплопроводности и удельную теплоемкость можно принять постоянными, то уравнение примет вид: , где - субстанциональная производная;

; - направление распределения тепловых потоков по координатам. При отсутствии внутренних источников теплоты: , где - температуропроводность.

Для неподвижных сред получаем дифференциальное уравнение теплопроводности (Фурье-Кирхгофа): .

Общий вид дифференциального уравнения энергии можно получит путем сопоставления уравнений: Производя замену в уравнении и проинтегрировав по времени, получим:

При умеренных скоростях течения жидкости, когда работа внешних сил и кинетическая энергия потока малы по сравнению с его энтальпией, уравнение существенно упрощается: , где - субстанциональная производная.

Для определения распределения температуры в потоке жидкости необходимо решить гидродинамическую задачу, то есть определить распределение скоростей в потоке жидкости.

Уравнение неразрывности

Одним из фундаментальных законов механики сплошных сред – закон сохранения массы любого индивидуального объема: ; или выражая его в дифференциальной форме, можно записать как: ;

в прямоугольных координатах: .

Для стационарных несжимаемых потоков , следовательно: .

Уравнение справедливо для любой однородной сплошной среды, когда нет поглощения массы, химических реакций, внутренней диффузии и других процессов, связанных с влиянием окружающей среды.

Если в смеси происходят хим. реакции, то массы компонентов могут меняться. В этом случае уравнение неразрывности для компонента многокомпонентной смеси можно записать в виде: или .

Здесь - изменение массы компонента смеси в единицу времени на единицу объема счет химической реакции.

В уравнение неразрывности входят три компонента скорости и одного этого уравнения не достаточно для определения скоростей в потоке жидкости.

Уравнение сохранения количества движения

Дифференциальное уравнение движение вязкой жидкости выводится на основании закона сохранения количества движения в применении к жидкости, протекающей через произвольный объем .

Скорость изменения главного вектора количества движения жидкости, находящейся в объеме , равна главному вектору массовых сил (веса) и поверхностных сил, действующих на поверхность (силы давлении и трения).

Главный вектор количества движения, находящейся в объеме определится как: .

Согласно закону сохранения движения: .

Учитывая, что , а - из уравнения неразрывности. Преобразовав интеграл по поверхности в интеграл по объему, согласно теореме Гаусса-Остроградского, имеем: .

Используя допущения о произвольности объема и оплошности среды, имеем: .

Учитывая, что получаем уравнение движения жидкости в напряжениях: .

Это уравнение в векторной форме в проекциях декартовых координат имеет вид:

;

;

;

 

Уравнения содержат 12 неизвестных: три компонента вектора скорости и девять компонентов вектора напряжения .

При движении вязкой жидкости в потоке действуют нормальное напряжение и напряжение сдвига. Нормальное напряжение обусловлено силами давления, а напряжения сдвига вызвано трением между слоями жидкости, движущимися с различными скоростями.

В соответствии с гипотезой Ньютона касательное напряжение (напряжение сдвига) в плоском потоке вязкой жидкости связано с производной от скорости по нормали к направлению потока простым соотношением: .

- коэффициент динамической вязкости, . .

- кинематическая вязкость, .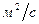

Если считать течение изотермическим и несжимаемым (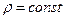; 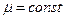) то общая запись уравнения примет вид: .

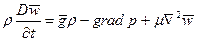В проекции по координатам имеем:

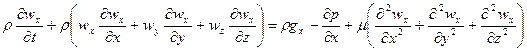
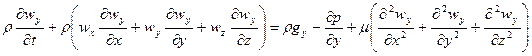
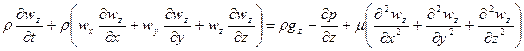
Таким образом, уравнение неразрывности и три уравнения движения в проекции на оси являются замкнутой системой уравнений, содержащей четыре неизвестных .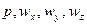

В том случае, когда плотность жидкости переменна и зависит от температуры, к уравнениям добавляется уравнение энергии и состояния, которые составляют замкнутую систему из шести уравнений с шестью неизвестными.

Уравнение состояния идеальных и реальных жидкостей

Простейшей механической моделью сплошной среды является модель идеальной жидкости, для которой характерно отсутствие сопротивлений (сил трения) при скольжении одного слоя жидкости по другому. Отдельные части взаимодействуют только в виде нормального давления, т. е. в любой точке идеальной жидкости касательные напряжения равны нулю.

Уравнением состояния для этой жидкости служат зависимости плотности от давления и температуры: 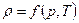. Для идеальных газов применимо уравнение Менделеева – Клайперона, вида: .

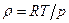Для капельных жидкостей сжимаемость чрезвычайно мала и в большом диапазоне давлений принимается линейная зависимость: .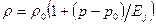

Здесь 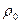плотность, соответствующая давлению 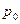; 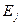- модуль объемного сжатия жидкости. В случае необходимости учета температурных факторов (тепловое расширение) уравнение состояния можно представить в виде: 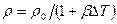, здесь 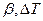- коэффициент объемного расширения жидкости и перепад температур.

Общая система уравнений гидромеханики

Из вышеизложенного следует, что движение сплошной среды, определяемые фундаментальными физическими законами описывается системой уравнений:

уравнение неразрывности:

уравнение сохранения количества движения: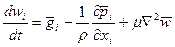

уравнение сохранения энергии:

уравнением состояния: .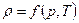

К системе дифференциальных уравнений добавляются условия однозначности и замыкающие зависимости.

 

Уравнения пограничного слоя

 

При продольном течении жидкости вдоль плоской поверхности происходит образование динамического пограничного слоя, в пределах которого вследствие сил трения скорость изменяется от значения скорости невозмущенного потока w0 на внешней границе слоя до нуля на самой поверхности теплообмена. По мере движения потока вдоль поверхности толщина пограничного слоя постепенно возрастает т.к. тормозящее воздействие стенки распространяется на боле далекие слои рис. 11.2.

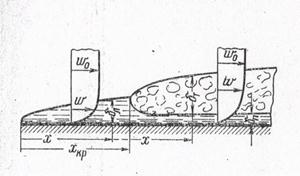
Рис.11.2 Схема движения при обтекании поверхности

На небольших расстояниях от передней кромки пограничный слой весьма тонкий и течение жидкости в нем носит струйный ламинарный характер. Толщина пограничного слоя определится: .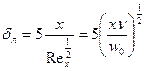

На некотором расстоянии хкр в пограничном слое начинают возникать вихри и течение принимает турбулентный характер. Толщина пограничного слоя определится: .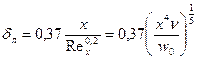

Вихри, существующие в пограничном слое интенсифицируют теплообмен, однако в непосредственной близости от поверхности они затухают и здесь сохраняется очень тонкий вязкий подслой.

Переход к турбулентному режиму течения жидкости в пограничном слое определяется критическим значением числа Рейнольдса: 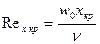, которое при продольном обтекании пластины принимают = 5 105.

В результате обобщения многочисленных экспериментов по теплоотдаче при обтекании пластин получены следующие расчетные зависимости:

При ламинарном режиме течения в пограничном слое местный коэффициента теплоотдачи определится: .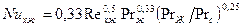

Для определения среднего коэффициента теплоотдачи применима зависимость: .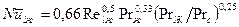

При турбулентном режиме течения в пограничном слое местный коэффициента теплоотдачи определится: .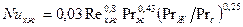

Средний коэффициент теплоотдачи по длине участка: .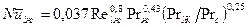

Здесь ; ; ; ; ; .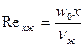

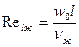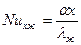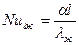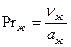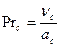Индексы «ж» и «с» указывают, что физические свойства теплоносителя относятся к температурам жидкости и стенки соответственно. Множитель 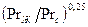представляет поправку учитывающую влияние изменения физических параметров теплоносителя с изменением температуры на теплоотдачу. Это множитель характеризует зависимость теплоотдачи от направления и величины теплового потока.

При нагревании капельной жидкости 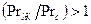, при охлаждении 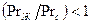. Для газов в частности воздуха расчетные формулы упрощаются и имеют вид: при ламинарном режиме течения в пограничном слое 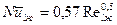; при турбулентном режиме .

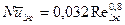Формулы применимы при постоянной температуре по длине пластины.


 

Решение дифференциальных уравнений сложная и трудоемкая задача, и она возможна при ограниченных простых случаев. Поэтому при исследовании конвективного теплообмена применяют метод теории подобия.

Теория подобия – это наука о подобных явлениях. Подобными явлениями называются такие физические явления, которые одинаковы качественно по форме и по содержанию, т.е. имеют одну физическую природу, развиваются под действием одинаковых сил и описываются одинаковыми по форме дифференциальными уравнениями и краевыми условиями. Обязательным условием подобия физических явлений должно быть геометрическое подобие систем, где эти явления протекают. Два физических явления будут подобны лишь в том случае, если будут подобны все величины, которые характеризуют их. Для всех подобных систем существуют безразмерные комплексы величин, которые называются критериями подобия.

Основные положения теории подобия формулируют в виде 3-х теорем подобия.

1 теорема: Подобные явления имеют одинаковые критерии подобия.

2 теорема: Любая зависимость между переменными, характеризующая какие-либо явления, может быть представлена, в форме зависимости между критериями подобия, составленными из этих переменных, которая будет называться критериальным уравнением.

3 теорема: Два явления подобны, если они имеют подобные условия однозначности и численно одинаковые определяющие критерии подобия. Условиями однозначности являются: наличие геометрического подобия систем; наличие одинаковых дифференциальных уравнений; существование единственного решения уравнения при заданных граничных условиях; известны численные значения коэффициентов и физических параметров.

Критериальные уравнения конвективного теплообмена.

Используя теорию подобия из системы дифференциальных уравнений можно получить уравнение теплоотдачи для конвективного теплообмена в случае отсутствия внутренних источников тепла в следующем критериальной форме: Nu = f2(Х; Ф; X0; Y0; Z0; Re; Gr; Pr) , где: X0; Y0; Z0 – безразмерные координаты;

Nu = α ·l0/λ - критерий Нуссельта (безразмерный коэффициент теплоотдачи), характеризует теплообмен между поверхностью стенки и жидкостью (газом);

Re = w·l0/ν - критерий Рейнольдса, характеризует соотношение сил инерции и вязкости и определяет характер течения жидкости (газа);

Gr = (β·g·l03·Δt)/ν2 - критерий Грасгофа, характеризует подьемную силу, возникающую в жидкости (газе) вследствие разности плотностей;

Pr = ν/а = (μ·cp)/λ - критерий Прандтля, характеризует физические свойства жидкости (газа) и является физической постоянной; l0 – определяющий размер (длина, высота, диаметр).

Pe = Re·Rr = w·l0/a - критерий Пекле, представляет собой среднюю меру отношения интенсивности переноса теплоты конвекцией к интенсивности переноса теплоты теплопроводностью.

Моделированием называется метод экспериментального изучения модели являения вместо натурного явления, при этом модель выбирают так чтобы получены результаты эксперимента можно было распространить на натурное явление. Моделирование применяют тогда когда трудно или невозможно изучить натурное явление по техническим или экономическим причинам.

Различают натурное моделирование - построение физической модели и проведение натурных испытаний с последующей обработкой результатов эксперимента. Математическое моделирование – построение расчетных схем и систем математических уравнений, описывающих протекающие процессы в изучаемом объекте.

Приведем критериальные уравнения теплоотдачи при свободном и вынужденном движении текучей среды, которые даны для средних значений коэффициентов теплоотдачи по поверхности стенки (академик М.А.Михеев):

1.Свободная конвекция в неограниченном пространстве.

а). Горизонтальная труба диаметром d при 103<(Gr··Pr)жd <108.

Nuжdср. = 0,5·(Grжd ·Pr ж)0,25 (Pr ж/Prст)0,25 .

б). Вертикальная труба и пластина:

ламинарное течение - 103<(Gr ·Pr)ж <109:

Nuжdср. = 0,75· (Grжd ·Pr ж)0,25·(Pr ж/Prст)0,25 .

турбулентное течение - (Gr ·Pr)ж > 109:

Nuжdср. = 0,15· (Grжd ·Pr ж)0,33 ·(Pr ж/Prст)0,25 .

Здесь значения Grжd и Pr ж берутся при температуре жидкости (газа), а Prст при температуре поверхности стенки.
Для воздуха Pr ж/Prст = 1 и формулы упрощаются.

2. Вынужденная конвекция.
Режим течения определяется по величине Re.
а). Течение жидкости в гладких трубах круглого сечения.
ламинарное течение – Re < 2100

Nuжdср. = 0,15·Reжd0,33·Prж0,33·(Grжd·Prж)0,1·(Prж/Prст)0,25·εl ,

где εl - коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы и зависит от отношения длины трубы к его диаметру (l/d).

Значения этого коэффициента представлена при ламинарном режиме:

l/d
εl 1,9 1,7 1,44 1,28 1,18 1,13 1,05 1,02 1,0

переходной режим – 2100 < Re < 104

Nuжdср. = К0·Prж0,43·(Prж/Prст)0,25·εl.

Коэффициент К0 зависит от критерия Рейнольдса Re и представлена:

Re·104 2,1 2,2 2,3 2,4 2,5
К0 1,9 2,2 3,3 3,8 4,4 6,0 10,3 15,5 19,5 27,0 33,3

турбулентное течение – Re = 104

Nuжdср. = 0,021· Reжd0,8·Prж0,43· (Prж/Prст)0,25·εl .

Таблица 10.3. Значение εl при турбулентном режиме.

l/d  
  Re = 2·103 Re = 2·104 Re = 2·105
1,9 1,51 1,28
1,70 1,40 1,22
1,44 1,27 1,15
1,28 1,18 1,10
1,18 1,13 1,08
1,13 1,11 1,06
1,05 1,05 1,03
1,02 1,02 1,02
1,00 1,00 1,00


б)Обтекание горизонтальной поверхности.
ламинарное течение – Re < 4·104

Nuжdср. = 0,66·Reжd0,5·Prж0,33 ·(Prж/Prст)0,25.

турбулентное течение – Re > 4·104

Nuжdср. = 0,037·Reжd0,5·Prж0,33 ·(Prж/Prст)0,25 .

в). Поперечное обтекание одиночной трубы (угол атаки = 900).
при Reжd = 5 - 103

Nuжdср. = 0,57·Reж0,5·Prж0,38 ·(Prж/Prст)0,25 .

при Reжd = 103 - 2·105

Nuжdср. = 0,25 ·Reж0,6·Prж0,38 ·(Prж/Prст)0,25 .

 

 

Теплопередачей называется передача теплоты от горячего теплоносителя к холодному теплоносителю через стенку, разделяющую эти теплоносители. Примерами теплопередачи являются: передача теплоты от греющей воды нагревательных элементов (отопительных систем) к воздуху помещения; передача теплоты от дымовых газов к воде через стенки кипятильных труб в паровых котлах; передача теплоты от раскаленных газов к охлаждающей воде (жидкости) через стенку цилиндра двигателя внутреннего сгорания; передача теплоты от внутреннего воздуха помещения к наружному воздуху и т. д. При этом ограждающая стенка является проводником теплоты, через которую теплота передается теплопроводностью, а от стенки к окружающей среде конвекцией и излучением. Поэтому процесс теплопередачи является сложным процессом теплообмена.

Стационарная теплопередача через однослойную и многослойную плоскую стенку при граничных условиях III рода

Рассмотрим процесс переноса теплоты от горячей движущейся жидкости с температурой T¥1 к холодной движущейся жидкости с температурой T¥2 через твердую стенку при 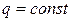Рис.9.5.

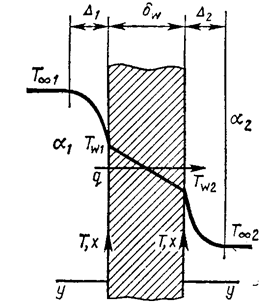
Рис.13.1 Схема теплопередачи через однослойную плоскую стенку

 

Плотность теплового потока от горячей жидкости: 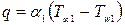. Плотность теплового потока через стенку: 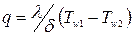. Плотность теплового потока к холодной жидкости: .

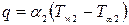Следовательно, плотность теплового потока от горячей среды к холодной определится как: 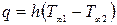или .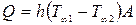

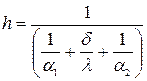- коэффициент теплопередачи однослойной плоской стенки. Для теплопередачи через многослойную плоскую стенку значение коэффициента теплопередачи примет вид: 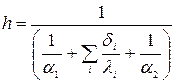, где i = число слоев стенки.

В формуле представлены следующие термические сопротивления:

термические сопротивления теплоотдачи на внешних поверхностях стенки 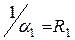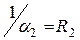; суммарное сопротивление теплопроводности n – слоев стенки: 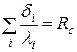; общее сопротивление теплопередачи: 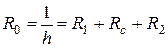. Температурное поле в однородной неограниченной стенке толщиной δ при λ=const: 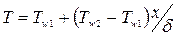, где x – текущая координата, при которой определяется температура T, .

 

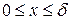Принцип расчета теплового потока через цилиндрическую стенку аналогична как и для плоской стенки. Рассмотрим однородную трубу (рис.12.2) с теплопроводностью λ, внутренний диаметр d1, наружный диаметр d2, длина l. Внутри трубы находится горячая среда с температурой t'ж, а снаружи холодная среда с температурой t''ж.

 

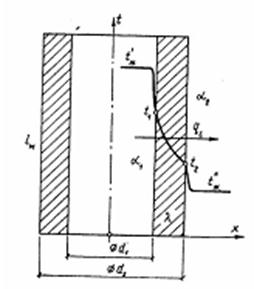
Рис.13.2 Схема теплопередачи через цилиндрическую стенку

Количество теплоты, переданной от горячей среды к внутренней стенке трубы по закону Ньютона-Рихмана имеет вид:

Q = p·d1·a1·l·(t'ж – t1),

где a1 – коэффициент теплоотдачи от горячей среды с температурой t'ж к поверхности стенки• с температурой t1; Тепловой поток, переданный через стенку трубы определяется по уравнению:

Q = 2·p·l·l·(t1 – t2) / ln (d2/d1).

Тепловой поток от второй поверхности стенки трубы к холодной среде определяется по формуле:

Q = p·d2·a2·l·(t1 - t''ж),

где a2 – коэффициент теплоотдачи от второй поверхности стенки к холодной среде с температурой t''ж. Решая эти три уравнения получаем:

Q = p l·(t'ж – t''ж) • К,

где Кl = 1/[1/(a1d1) + 1/(2lln(d2/d1) + 1/(a2d2)]

- линейный коэффициент теплопередачи,

или Rl = 1/ Кl = [1/(a1d1) + 1/(2lln(d2/d1) + 1/(a2d2)]

полное линейное термическое сопротивление теплопередачи через однослойную цилиндрическую стенку.

1/(a1d1), 1/(a2d2) – термические сопротивления теплоотдачи поверхностей стенки;

1/(2lln(d2/d1) - термическое сопротивление стенки.

Для многослойной (n слоев) цилиндрической стенки полное линейное термическое сопротивление будет определяться по следующей формуле:

Rl = 1/ Кl = [1/(a1d1) + 1/(2l1ln(d2/d1) + 1/(2l3ln(d3/d2) + …
+ 1/(2lnln(dn+1/dn) + 1/(a2dn)] – (12.15)

 

Тепловая изоляция. Критический диаметр тепловой изоляции.

Тепловая изоляция служит для снижения потерь тепла при теплообмене в процессах движения теплоносителей по каналам или перемещения рабочих тел в элементах технических систем, устройств.

Проверка пригодности материала изоляции для уменьшения тепловых потерь от трубопровода в окружающую среду производится по критическому диаметру: 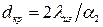.Здесь 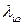- теплопроводность материала изоляции; 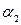- коэффициент теплоотдачи от наружной поверхности в окружающую среду. Если 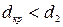(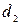- наружный диаметр неизолированного трубопровода), то покрытие трубы такой изоляцией будет снижать теплопотери в окружающую среду. Если 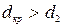, то применение такого изоляционного материала нецелесообразно и следует подобрать другой материал или применить многослойную изоляцию. Условие выбора теплоизоляционного материала для снижения теплопотерь от трубопровода, покрытого слоем изоляции: .

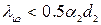Теплообменные аппараты (ТА) – устройства, предназначенные для передачи теплоты от более нагретого теплоносителя к менее нагретому теплоносителю. Классификации ТА приведена на Рис. 13.3.

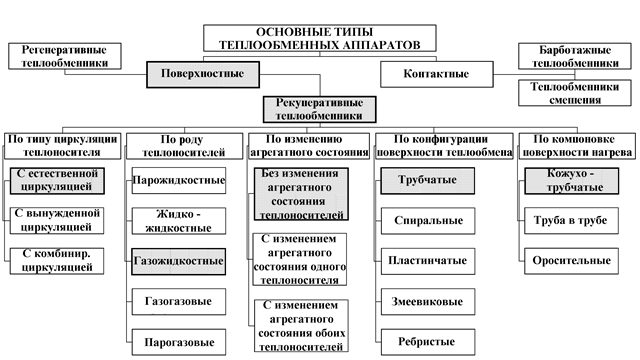
Рис. 13.3 Классификации теплообменных аппаратов

В качестве теплоносителей в тепловых аппаратах используются разнообразные капельные и упругие жидкости в самом широком диапазоне давлений и температур. По принципу работы аппараты делят на регенеративные, смесительные и рекуперативные. В регенеративных аппаратах горячий теплоноситель отдает свою теплоту аккумулирующему устройству, которое в свою очередь периодически отдает теплоту второй жидкости - холодному теплоносителю, т. е. одна и та же поверхность нагрева омывается то горячей, то холодной жидкостью. В смесительных аппаратах передача теплоты от горячей к холодной жидкости происходит при непосредственном смешении обеих жидкостей, например смешивающие конденсаторы. Особенно широкое развитие во всех областях техники получили рекуперативные аппараты, в которых теплота от горячей к холодной жидкости передается через разделительную стенку. Только такие аппараты будут рассмотрены в дальнейшем. Теплообменные аппараты могут иметь самые разнообразные назначения — паровые котлы, конденсаторы, пароперегреватели, приборы центрального отопления и т. д. Теплообменные аппараты в большинстве случаев значительно отличаются друг - от друга как по своим формам и размерам, так и по применяемым в них рабочим телам. Несмотря на большое разнообразие теплообменных аппаратов, основные положения теплового расчета для них остаются общими.

В теплообменных аппаратах движение жидкости осуществляется по трем основным схемам.

Если направление движения горячего и холодного теплоносителей совпадают, то такое движение называется прямотоком (рис.13.4,а).

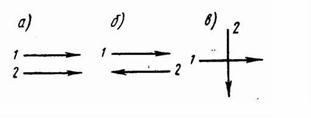
Рис. 13.4 Схемы направлений жвижения

Если направление движения горячего теплоносителя противоположно движению холодного теплоносителя, то такое движение называется противотоком (рис.13.4,б). Если же горячий теплоноситель движется перпендикулярно движению холодного теплоносителя, то такое движение называется перекрестным током (рис.13.4,в). Кроме этих основных схем движения жидкостей, в теплообменных аппаратах применяют более сложные схемы движения, включающие все три основные схемы.

Схема однотрубного теплообменного аппарата и распределение температур по дине приведена на Рис. 13.5.

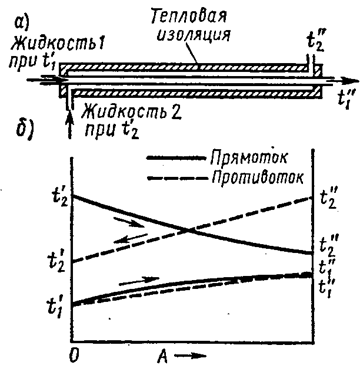
Рис. 13.5 Схема однотрубного теплообменного аппарата и распределение температур по его дине

 

Если нагреваемая жидкость 1 и греющая жидкость 2 движутся водном направлении – прямоток; в противоположном – противоток;

Количество теплоты определится как: .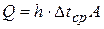

где 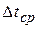- средняя разность температур жидкостей – средний температурный напор; средний логарифмический температурный напор: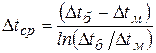

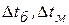- больший и меньший температурные напоры между жидкостями вне зависимости от схемы движения жидкости (прям или противоток).

для прямотока: ; ;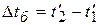

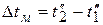для противотока: ; ;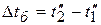

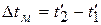При 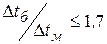то средний температурный напор можно определять как средний аритмический: .

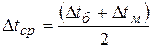Площадь поверхности нагрева определится как:

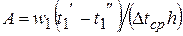или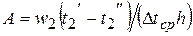

КПД теплообменного аппарата: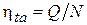

здесь 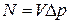V – объемный расход теплоносителя м3/с; Dp – полное гидравлическое сопротивление движению теплоносителя, Па.Гидравлическое сопротивление определяется как: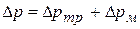

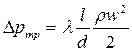- сопротивление терния (путевые потери), Па;

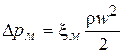- местное сопротивление (местные потери), Па;

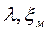- коэффициент сопротивлений путевых и местных; 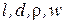- длина, внутренний диаметр канала, плотность, скорость движения теплоносителя.

 


 

14. Физическая сущность лучистого теплообмена, виды потоков излучения и радиационные характеристики тел. Основные законы теплового излучения (Планка, Вина, Стефана-Больцмана, Кирхгофа). Эффективное излучение. Приведённый коэффициент излучения системы тел. Лучистый теплообмен между телами, разделенными прозрачной средой.

 

Тепловое излучение – сложный процесс, при котором дважды происходит преобразование энергии: сначала переход тепловой энергии в излучение электромагнитных волн – эмиссия, затем движение волн (фотонов) и поглощение электромагнитных колебаний телом или средой (абсорбция).

Лучистая энергия возникает за счет энергии других видов в результате сложных молекулярных и внутриатомных процессов. Природа всех лучей одинакова. Они представляют собой распространяющиеся в пространстве электромагнитные волны. Источником теплового излучения является внутренняя энергия нагретого тела. Количество лучистой энергии в основном зависит от физических свойств и температуры излучающего тела. Электромагнитные волны различаются между собой длиной волны.

В зависимости от длины волны λ лучи обладают различными свойствами. Наименьшей длиной волны обладают космические лучи λ = (0,1 – 10)оА (где оА — ангстрем, единица длины, 1оА = 10-10м). Гамма-лучи, испускаемые радиоактивными веществами, имеют длину волны до 10оА ; лучи Рентгена – λ = (10-200) оА; ультрафиолетовые лучи – λ = (200оА - 0,4 мк (мк — микрон, 1 мк — 0,001 мм), световые лучи – λ = (0,4-0,8)мк, инфракрасные или тепловые лучи – λ = (0,8 – 400) мк, радио или электромагнитные лучи - λ > 400 мк. Из всех лучей наибольший интерес для теплопередачи представляют тепловые лучи с λ = (0,8 – 40) мк.

Лучеиспускание свойственно всем телам, и каждое из них излучает и поглощает энергию непрерывно, если температура его не равна 0°К. При одинаковых или различных температурах между телами, расположенными как угодно в пространстве, существует непрерывный лучистый теплообмен.

При температурном равновесии тел количество отдаваемой лучистой энергии будет равно количеству поглощаемой лучистой энергии. Спектр излучения большинства твердых и жидких тел непрерывен. Эти тела испускают лучи всех длин волн от малых до больших. Спектр излучения газов имеет линейчатый характер. Газы испускают лучи не всех длин волн. Такое излучение называется селективным (избирательным). Излучение газов носит объемный характер. Суммарное излучение с поверхности тела по всем направлениям полусферического пространства и по всем длинам волн спектра называется интегральным или полным лучистым потоком (Q).

Поток монохромного или спектрального излучения - лучистая энергия, испускаемаяв пределах некоторого (одного или нескольких) участка длин волн из всего диапазона.

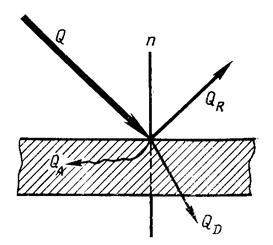
Каждое тело способно не только излучать, но и отражать, поглощать и пропускать через себя падающие лучи от другого тела. Если обозначить общее количество лучистой энергии, падающей на тело, через Q, то часть энергии, равная А, поглотится телом, часть, равная R, отразится, а часть, равная D, пройдет сквозь тело. Отсюда Q = QA + QR + QD)

или A + R + D = 1. Величину А называют коэффициентом поглощения. 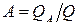представляет собой отношение поглощенной лучистой энергии ко всей лучистой энергии, падающей на тело. Величину R называют коэффициентом отражения. 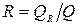есть отношение отраженной лучистой энергии ко всей падающей. Величину D называют коэффициентом проницаемости. 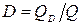есть отношение прошедшей сквозь тело лучистой энергии ко всей лучистой энергии, падающей на тело. Для большинства твердых тел, практически не пропускающих сквозь себя лучистую энергию, А + R = 1. Газы (двухатомные) при умеренных температурах – проницаемые среды 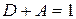. Если поверхность поглощает все падающие на нее лучи, т. е. А = 1, R = 0 и D = 0, то такую поверхность называют абсолютно черной. Если поверхность отражает полностью все падающие на нее лучи, то такую поверхность называют абсолютно белой. При этом R = 1, А = 0, D = 0. Если тело абсолютно проницаемое для тепловых лучей, то D = 1, R = 0 и A = 0.

В природе абсолютно черных, белых и прозрачных тел не существует, тем не менее понятие о них является очень важным для сравнения с реальными поверхностями. Кварц для тепловых лучей непрозрачен, а для световых и ультрафиолетовых лучей прозрачен. Каменная соль прозрачна для тепловых лучей и непрозрачна для ультрафиолетовых лучей. Оконное стекло прозрачно для световых лучей, а для ультрафиолетовых и тепловых почти непрозрачно. Белая поверхность (ткань, краска) хорошо отражает лишь видимые лучи, а тепловые лучи поглощает также хорошо, как и темная.

Таким образом, свойство тел поглощать или отражать тепловые лучи зависят в основном от состояния поверхности, а не от ее цвета. Если поверхность отражает лучи под тем же углом, под которым они падают на нее, то такую поверхность называют зеркальной. Если падающий луч при отражении расщепляется на множество лучей, идущих по всевозможным направлениям, то такое отражение называют диффузным (например поверхность мела). При исследовании лучистых потоков большое значение имеет распределение лучистой энергии, испускаемой абсолютно черным телом по отдельным длинам волн спектра.

Для жидких и твердых тел характерный слой пропускания составляет микроны, соответственно. Тела, подчиняющиеся данному закону – серые тела. Серые тела характеризуются непрерывным распределением энергии в спектре собственного излучения, подобно распределению энергии в спектре абсолютно черного тела при одинаковых температурах.

Коэффициентом черноты серого тела 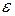называют величину равную отношению поверхностных плотностей потоков интегрального излучения 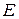серого тела и 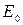абсолютно черного тела: .

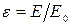Поверхностная плотность потока интегрального излучения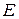(Вт/м2) – величина, равная отношению лучистого потока 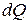, испускаемого элементарной площадкой :

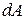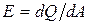
Спектральная плотность потока излучения 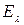- величина равная отношению плотности лучистого потока, испускаемого в мнтервале длин волн 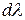, к величине этого интервала: .

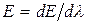Виды лучистых потоков.

Для определения параметров сложного процесса лучистого теплообмена вводят модель лучистого теплообмена для которой используют следующие виды потоков Рис.14.2.

 

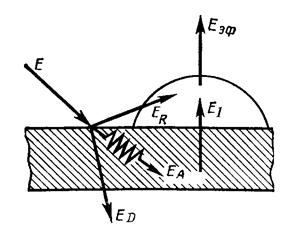
Рис. 14.2 Составляющие сложного процесса лучистого теплообмена

 

поток собственного излучения (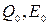) определяется природой тела и его температурой;

поток падающего излучения () частично поглощается телом, частично отражается, частично проходит сквозь тело;

поток поглощенного излучения (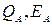) - та часть падающей энергии излучения на тело, которая поглощается им: ;

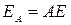поток отраженного излучения (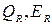) – та часть падающей энергии излучения на тело, которая отражается им: ;

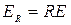поток пропускаемо излучения (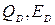)та часть падающей энергии излучения на тело, которая проходит сквозь него: ;

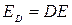Таким образом, по закону сохранения энергии: .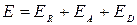

Поток эффективного излучения – это сумма плотностей потоков собственного 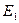и отображенного излучения 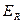, испускаемого поверхностью данного тела и отраженного излучения: .

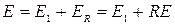Поток результирующего излучения – это количество теплоты, перенесенное от одного тела к другому в результате теплообмена излучением, то есть разность между лучистыми потоками, получаемым и отдаваемым телом: .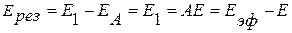

Интенсивность излучения.

Каждой длине волны лучей, при определенной температуре, соответствует определенная интенсивность излучения. Она определяется отношением плотности потока излучения, взятой в бесконечно малом интервале длин волн, к этому интервалу: .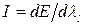

 

Законы теплового излучения Планка, Вина, Стефана-Больцмана, Кирхгофа, Ламберта

Закон Планка. Интенсивности излучения абсолютно черного тела Isλ и любого реального тела Iλ зависят от температуры и длины волны. Абсолютно черное тело при данной температуре испускает лучи всех длин волн от λ = 0 до λ = ∞. Если каким-либо образом отделить лучи с разными длинами волн друг от друга и измерить энергию каждого луча, то окажется, что распределение энергии вдоль спектра различно. По мере увеличения длины волны энергия лучей возрастает, при некоторой длине волны достигает максимума, затем убывает. Кроме того, для луча одной и той же длины волны энергия его увеличивается с возрастанием температуры тела, испускающего лучи (рис.14.3).

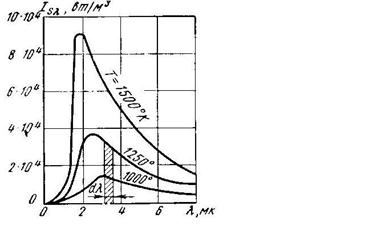
Из рис.14.3 видно, что для любой температуры интенсивность излучения Isλ возрастает от нуля (при λ=0) до своего наибольшего значения, а затем убывает до нуля (при λ=∞). При повышении температуры интенсивность излучения для каждой длины волны возрастает.

Планк установил следующий закон изменения спектральной плотности потока излучения абсолютно черного тела 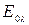в вакууме от абсолютной температуры 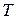и длины волны 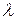в форме: 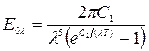, здесь константы , .

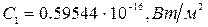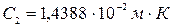Закон смещения Вина. Кроме того из рис.14.3 максимумы кривых с повышением температуры смещаются в сторону более коротких волн. Длина волны lmax, отвечающая максимальному значению Isl, определяется законом смещения Вина: lmax = C3 / T.

С увеличением температуры lmax уменьшается. Пользуясь законом смещения Вина, можно измерять высокие температуры тел на расстоянии, например, расплавленных металлов, космических тел и др. Из Закон Вина следует связь между длиной волны 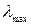, на которую приходится максимум величины 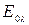(спектральной плотности потока излучения абсолютно черного тела) и его температуры в форме: 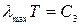. Здесь 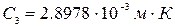- константа.

Закон Стефана-Больцмана. Планк установил, что каждой длине волны соответствует определенная интенсивность излучения, которая увеличивается с возрастанием температуры. Тепловой поток, излучаемый единицей поверхности черного тела в интервале длин волн от λ до λ + dλ, может быть определен из уравнения: dEs = Isλ*dλ.

Элементарная площадка на рис.14.3, ограниченная кривой Т = const, основанием dλ ординатами λ и λ + dλ (Isλ) определяет количество лучистой энергии dEs и называется лучеиспускательной способностью абсолютно черного тела для длин волн dλ. Вся же площадь между любой кривой Т = const и осью абсцисс равна интегральному излучению черного тела в пределах от λ = 0 до λ = ∞ при данной температуре. Подставляя в уравнение закон Планка и интегрируя от от λ= 0 до λ = ∞, найдем, что интегральное излучение (тепловой поток) абсолютно черного тела прямо пропорционально четвертой степени его абсолютной температуры (закон Стефана-Больцмана).

Es = Сs (Т/100)4,

где Сs = 5,67 Вт/(м2*К4) - коэффициент излучения абсолютно черного тела

Излучение реальных тел также зависит от температуры и длины волны. Чтобы законы излучения черного тела можно было применить для реальных тел, вводится понятие о сером теле и сером излучении. Под серым излучением понимают такое, которое аналогично излучению черного тела имеет сплошной спектр, но интенсивность лучей для каждой длины волны Iλ при любой температуре составляет неизменную долю от интенсивности излучения черного тела Isλ, т.е. существует отношение:

Iλ / Isλ = ɛ = const.

Величину ɛ называют степенью черноты. Она зависит от физических свойств тела. Степень черноты серых тел всегда меньше единицы. Большинство реальных твердых тел с определенной степенью точности можно считать серыми телами, а их излучение — серым излучением. Энергия интегрального излучения серого тела равна:

Е = ɛ*Es = С* (Т/100)4.

Лучеиспускательная способность серого тела составляет долю, равную е от лучеиспускательной способности черного тела. Величину С = ɛ*Es называют коэффициентом излучения серого тела. Величина С реальных тел в общем случае зависит не только от физических свойств тела, но и от состояния поверхности или от ее шероховатости, а также от температуры и длины волны. Значения коэффициентов излучения и степеней черноты тел берут из таблиц.

Степень черноты полного нормального излучения

для различных материалов

Наименование материала t ,°С ɛ
Алюминий полированный 50—500 0,04—0,06
Бронза 0,1
Железо листовое оцинкованное, блестящее 0,23
Жесть белая, старая 0,28
Золото полированное 200 - 600 0,02—0,03
Латунь матовая 20-350 0,22
Медь полированная 50—100 0,02
Никель полированный 200—400 0,07—0,09
Олово блестящее 20—50 0,04—0,06
Серебро полированное 200—600 0,02—0,03
Стальной листовой прокат 0,56
Сталь окисленная 200—600 0,8
Сталь сильно окисленная 0,98
Чугунное литье 0,81
Асбестовый картон 0,96
Дерево строганое 0,8—0,9
Кирпич огнеупорный 500—1000 0,8—0,9
Кирпич шамотный 0,75
Кирпич красный, шероховатый 0,88—0,93
Лак черный, матовый 40—100 0,96—0,98
Лак белый 40—100 0:8—0,95
Масляные краски различных цветов . . . 0,92—0,96
Сажа ламповая 20—400 0,95
Стекло 20—100 0,91—0,94
Эмаль белая 0,9

Закон Кирхгофа – устанавливает связь между излучательной и поглащательной способностью тела. Отношение потока излучения любого тела 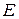к его коэффициенту поглощения 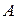при данной температуре не зависит от природы тела и равно потоку излучения абсолютно черного тела