Лаплас жіктеуі ( теоремасы).
Реттері үлкен анықтауыштарды есептеу қиындыққа келтіреді, сондықтан оларды есептеу үшін анықтауыштардың қасиеттерін қолданады және Лапластың жіктеу теоремасын. Лапластың теоремасы берілген анықтауыштың ретін төмендетеді.
n -ші ретті анықтауыш берілсін делік:
= 
Осы анықтауыштың 
элементінің миноры 
деп, анықтауышының і жатық жолы мен j тік жолын сызып тастағаннан кейін қалатын (n-1) ретті анықтауышты айтады.
= 
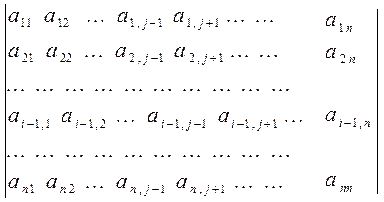(5)
Берілген анықтауыштың элементінің алгебралық толықтауышы 
деп, осы элементтің миноры мен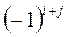 
өрнегінің көбейтіндісін айтады.
= 
(6)
Мысал. Үшінші ретті анықтауыш берілген.
= 
Осы анықтауыштың 
элементінің минорын тауып оның алгебралық толықтауыштарын есептеңіз.
Шешуі:
; 
Лаплас теоремасы (Лапластың жіктеу теоремасы). Анықтауыштың кез келген жатық (тік) жолдарының элементтерімен оның алгебралық толықтауыштарының көбейтінділерінің қосындысы осы анықтауыштың мәніне тең, яғни
(7)
Кез келген n-ші ретті анықтауыштарды есептеу үшін олардың тік немесе жатық элементтері бойынша жіктеу арқылы есептеуге болады. Бұл әдістің мақсаты – анықтауыштардың ретін төмендету. Лаплас теоремасы реті төртке тең немесе төрттен артық анықтауыштарды есептеуде қолданылады. (7) формуланы қолдану арқылы анықтауыштың ретін бірге төмендете отырып өзімізге белгілі болған үшінші немесе екінші ретті анықтауыштарға келтіруге болады және анықтауыштың қасиетін пайдаланып жіктейін деп отырған тік немесе жатық жолдын бір элементінен басқасы нөльге айналдыру арқылы есептеуді жеңілдетуге болады.
Мысал. Төмендегі төртінші ретті анықтауышты есептеңдер:
Анықтауышты екінші жатық жолының элементтері бойынша жіктеп есептейік:
=
=
4.Матрицалар және олардың түрлері.
Анықтама. m*n-ретті матрица деп, m-жатық және n-тік жолдардан анықталған тік бұрышты кестені айтады, ол мына түрде белгіленеді:
A=
(1)Немесе 
; 
; 
Мұндағы -матрицаның элементтері деп аталады, бірінші индекс і матрицаның жатық жолының, ал екінші индекс j-тік жолының нөмерін анықтайды. Матрицалар латын алфавитінің бас әріптерімен (A,B,C...) белгіленеді, ал матрицалардың элементтері – кіші әріптерімен: , 
.
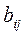Матрицаның дербес түрлері.
Егер матрицаның жатық жолының саны тік жолының санына тең болса, яғни: m=n, онда ол матрица квадратты (квадрат) матрица деп аталады, яғни:
A=
(2)
Бұл жағдайда А матрица n-ші ретті матрица деп аталады.
Квадратты матрицаның 
элементтері оның бас диагоналы, ал 
элементтері қосалқы диагоналы деп аталады.
Егер матрицаның барлық элементтері нөлге тең болса, онда ол матрица нөл матрица деп аталады және ол 0 символымен белгіленеді:
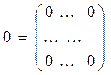
Егер матрицаның бас диагоналының элементтерінен өзге элементтері нөлге тең болса: 
егер 
егер 
Онда ол матрица диагоналды матрица деп аталады және мына түрде белгіленеді:
Егер диагоналды матрицаның барлық элементтері бірге тең болса: 
онда ол бірлік матрица деп аталады және ол Е символымен белгіленеді. Мысалы, үшінші ретті бірлік матрица мынадай болады:
Е =
Егер бас диагоналдан төмен орналасқан немесе жоғары орналасқан элементтері нөлге тең болса, онда квадратты:
A=
немесе A=
матрица үшбұрышты матрица деп аталады.
Егер матрица бір тік (жатық) жолдан анықталса, онда ол матрица тік (жатық) жолды матрица деп аталады және ол
; 
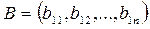
символымен белгіленеді.
Бірдей ретті A мен B матрицалар тең деп аталады, егер олардың сәйкес элементтері тең болса.
Біз кез келген m*n ретті:
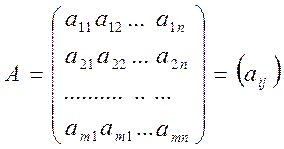
матрицаны қарастырайық.
Анықтама. 
матрица m*n ретті А матрицасының транспонирленген матрицасы деп аталады, егер 
теңдігі орындалса, және ол былай белгіленеді:
(3) 
Осы анықтамадан, А-матрицасының жатық жолдарының элементтерін оның сәйкес тік жолдарының сәйкес элементтерімен орын алмастыру нәтижесінде берілген А матрицасының транспонирленген матрица n* m-ретті матрица екендігі шығады.
Берілген квадрат А матрицаның анықтауышы немесе детерминанты мына түрде белгіленеді
немесе det A=
Анықтама. Егер А матрицасының анықтауышы нөлге тең болмаса, яғни 
онда А матрица ерекше емес матрица деп аталады, ал егер 
болса, онда ол ерекше матрица деп аталады.
5. Матрицаларға қолданылатын амалдар.
Матрицаларға қосу, алу, көбейту және нақты санды матрицаға көбейту амалдары орындалады.
1. Матрицаларды қосу және азайту.
Бірдей ретті мен 
матрицаларының қосындысы (айырмасы) деп сол ретті 
матрицасын айтады: 
және оның кез келген элементтері мына формуладан анықталады: 
Мысалы: 
және 
берілген болса, олардың қосындысы былай есептелінеді: 
Ал енді A және B матрицалардын айырмасын табайық:
2. Матрицаларды нақты санға көбейту:
Кез келген А матрицаны 
нақты санына көбейту үшін матрицаның барлық элементтерін сол санға көбейту керек. Мысалы, егер 
және 
онда: 
3. Матрицаларды көбейту.
Берілген m*n ретті А матрицаның n*k ретті В матрицаға көбейтіндісі деп, m*n ретті С матрицаны айтады: 
Ал оның кез келген элементтері 
(4) 
Осы анықтамадан А матрицаны В матрицаға көбейтуге болады, егер А матрицаның тік жолының саны В матрицасының жатық жолының санына тең болса, бұл жағдайда матрицаның жатық жолының саны А матрицаның жатық жолының санына тең, ал оның тік жолының саны В матрицаның тік жолының санына тең.
Мысал: 
; 
және 
көбейтінділерді табуға бола ма? 
. Бұл жағдайда А матрицаны В матрицаға көбейтуге болады, себебі А матрицаның тік жолының саны В матрицаның жатық жолдар санына тең:
A
B=
=
=
=
Ал В матрицаны А матрицаға көбейтуге болмайды, себебі В матрицаның тік жолының саны А матрицасының жатық жолының санына тең емес.
Енді екінші ретті А мен В квадрат матрицаларының көбейтінділерін қарастырайық, мысалы:
A=
; B=
 |
AB= =
=
 |
BA= =
=
Сонымен, AB=ал BA=
Демек, егер А*В мен В*А көбейтінділері бар болғанымен де олар өзара тең емес, яғни 
. Жалпы жағдайда матрицалар көбейтінділеріне ауыстырымдылық қасиет орындалмайды. Сонымен (4) формуладан матрицалардың көбейтінділеріне мына қасиеттер орындалады (егер көбейтінділер бар болса):
1) терімділік қасиет: 
2) үлестірімділік қасиет: 
Тікелей көбейту арқылы А*Е=Е*А=А теңдігі орындалатындығына оңай көз жеткіземіз.