Цикл Карно

Равновесные термодинамические процессы и их обратимость. Графическое изображение процессов. Рабочая и тепловая диаграммы. Политропные процессы, их исследование и графическое изображение в рабочей диаграмме.

Энергетические характеристики термодинамических систем: теплота, работа, внутренняя энергия, энтальпия. Понятие функции процесса и функции состояния. Эквивалентность теплоты и работы. Сущность и уравнение первого закона термодинамики.

Content-addressable storage (CAS)

Content-addressable storage (CAS) — архитектура хранения, в которой адресация осуществляется образом хранимых данных. Образ данных хэшируется и хэш используется для его нахождения на устройствах или системах хранения. По сути данные записываются в BLOB-поля специализированной базы данных, а вычисленный хэш используется как индексный ключ базы, по которому осушествляется быстрый поиск содержимого. Построение системы хранения как базы данных позволило применять к процессам доступа и хранения данных методы работы с базами (версионность хранения, дедупликация). Справедливости ради следует также упомянуть, что ранее такие формы организации информации уже применялись на практике, например файловая система OS VMS (применявшаяся на DEC VAX, впоследствии OpenVMS) была организована как своеобразная база данных.

Архитектура обладает большой устойчивостью к дубликатам, а так же может быть выполнена децентрализованно, что дает ей существенную надежность. Однако серьезным недостатком такого способа организации хранения следует назвать невысокое быстродействие, не позволяющее применять CAS в качестве primary storage. В настоящий момент CAS заняли свое место в системах архивного, долговременного и неизменяемого хранения. Наиболее известным производителем CAS-систем на рынке является компания EMC и ее системы серии Centera.

 


 

 

Теплота – энергия, передаваемая более нагретым телом менее нагретому, не связанная с переносом вещества и совершением работы.

Теплообмен – форма передачи энергии от одних тел к другим путем теплопроводности, конвекции и излучения.

Теплообмен между телами осуществляется только в условиях, когда тела имеют разную температуру. Количество теплоты, получаемое телом в результате теплообмена, зависит от вида процесса, от того пути, по которому система переходит от одного состояния в другое. Поэтому элементарные количество теплоты рассматриваются как бесконечно малые величины, не являющиеся полным дифференциалом.

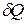- элементарное количество теплоты, полученное или отданное телом в результате теплообмена [Дж]; - элементарное количество теплоты, отнесенное к еденице массы вещества (удельное количество теплоты) [Дж/(кг)]. Теплота, подводимая к телу считается положительной , а отводимая от тела – отрицательной .

 

Работа – энергетическое воздействие одного тела на другое, не связанное с переносом теплоты и вещества. В общем случае работа (механика) – произведение проекции силы на элементарное перемещение точки приложения силы.

Рис.2.1 Элементарная механическая работа линейного перемещения

 

Работа зависит от вида процесса. В отличие от внутренней энергии работа не определяется начальной и конечной точками процесса, не является функцией состояния, следовательно, и не является полным дифференциалом. Для изменения элементарной работы используется символ , а не . В простейшем случае элементарная работа сжимаемых тел определяется в зависимости от давления и изменения объема.

       
 
Рис. 2.2. Работа расширения в цилиндре поршневой машины
 
Рис. 2.3. Работа расширения газа при изменении объема тела

 


. Следовательно, расчетное значение для элементарной работы изменения объема в обратимом процессе определится как: .

Работу, рассчитанную по полученному выражению, будем называть термодинамической работой. Эта работа в координатах определяется площадью, ограниченной линией процесса, и координатами точек начала и конца процесса Рис. 2.4. Работа считается положительной, если система совершает ее над внешними телами, т.е. (Рис. 2.4 а) и отрицательной , если внешние тела совершают работу над системой, т.е. (Рис. 2.4 б).

а) б)

Рис. 2.4 Термодинамическая работа изменения объема тела

Представленная работа на Рис. 2.5, наглядно показывает, что она зависит от пути процесса, т.е. как шел процесс от точки 1 в точку 2 .

 

;

Рис. 2.5 Зависимость работы от пути перехода процесса

 

Обычно в курсе технической термодинамики оперируют удельными величинами, так термодинамическая работа изменения объема 1 кг газообразного рабочего тела определится: и соответственно .

Эффективная работа реального процесса определится как разность между обратимой работой изменения объема и работой необратимых потерь : ;

Работа, потерянная в необратимых процессах , превращается в теплоту внутреннего теплообмена.

 

Потенциальная работа

Потенциальной работой принято называть работу по обратимому перемещению объема рабочего тела (жидкостей, паров или газов) из области одного давления в область другого давления . Основные условные слагаемые потенциальной работы Рис. 2.6 - наполнение; - расширение (сжатие); - выталкивание.

 

- наполнение; - расширение (сжатие); - выталкивание.

 

Рис. 2.6 Слагаемые потенциальной работы по перемещению газа из области давления в область давления

 

Элементарная потенциальная работа и соответственно элементарная удельная потенциальная работа определятся как:

Потенциальная работа имеет положительный знак при перемещении рабочего тела из области большего давления в область меньшего давления , и, наоборот при работа отрицательна.

Потенциальная работа, как и термодинамическая, измеряется площадью в координатах Рис.2.7. и определяется соответственно:

 

 

Рис. 2.7. Потенциальная работа перемещения вещества из области давления в область давления

Применительно к магистральным газопроводам при перемещении газа удельная потенциальная работа определиться:

Как и термодинамическая работа в обратимом процессе потенциальная работа - сумма эффективной работы и работы необратимых потерь : ;

Потенциальная работа необратимых потерь , превращается в теплоту внутреннего теплообмена. Эффективная потенциальная работа непосредственно передается телам внешней системы, а и используется для изменения энергии внешнего положения рабочего тела.

Внутренней энергией тела или системы тел называют совокупность всех видов энергии, заключенной в рассматриваемой системе. Внутренняя энергия обозначается как U [Дж] и удельная - u [Дж/(кг)] и является функцией состояния системы.

Согласно закону сохранения энергии внутренняя энергия системы в каждом своем состоянии имеет только одно определенное значение, т.е. система сама для себя не может служить источником энергии. Внутри системы возможны различные преобразования энергии, однако в целом внутренняя энергия системы не изменяется. Если бы система имела различные значения внутренней энергии, то можно было отнять эту разность, при этом состояние системы не изменилось, что противоречит закону сохранения энергии. Следовательно, энергия системы есть функция состояния и не зависит от пути перехода системы из одного состояния в другое, а - полный дифференциал.

Внутренняя энергия определяется температурой и деформационными координатами системы: . Теплота и работа являются формами переноса внутренней энергии.

Первый закон термодинамики (начало) является по существу законом преобразования и сохранения энергии применительно к процессам, изучаемым в термодинамике, он формулируется как: «Невозможен процесс возникновения или исчезновения энергии».

Открытию данного закона предшествовали многочисленные эксперименты и теоретические исследования в области физики и химии, развитие тепловых двигателей 18-19 столетиях, установление принципа, исключающего построение вечного двигателя первого рода (1975 г.).

Одним из шагов на пути открытия первого закона термодинамики является открытие русским ученым Г.И. Гессом (1840) закона «О независимости теплового эффекта химических реакций от промежуточных или от последовательности этих реакций», суть которого заключается в том, что общий тепловой эффект химических реакций можно рассматривать как алгебраическую сумму тепловых эффектов ряда последовательных химических реакций, если начальные и конечные состояния системы одинаковы в условиях равенства их термодинамических путей процесса.

Завершающим этапом к открытию закона послужило открытие (1842-1850 г. Р.Майер, Д.Джоуль, Г. Гельмгольц) принципа эквивалентности, согласно которому превращение теплоты в работу и работы в теплоту осуществляется всегда в одном и том же постоянном количественном соотношении: . В дальнейшем было установлено, что тепловой эквивалент работы сохраняет свое постоянное значение не зависимо от того, как получена теплота, каков вид работы, какова температура, следовательно: .

Приведем наиболее общую и известную формулировку первого закона термодинамики: «Невозможно построить «вечный двигатель первого рода» - иллюзорного аппарата, способного непрерывно совершать полезную работу без получения энергии от какого-либо источника».

Первое начало термодинамики устанавливает, что внутренняя энергия системы является однозначной функцией ее состояния, и изменятся только под влиянием внешних воздействий. При этом все возможные виды энергетического воздействия сводятся к формам передачи теплоты и работы.

Различие между теплотой и работой состоит не только в том, что они являются различными формами передачи энергии, но и в принципиальной особенности работы как формы энергетического взаимодействия (мех, электр, хим. и т.д.).

Теплота представляет собой такую форму передачи энергии, которая определяется непосредственным контактом между телами с различной температурой или лучистым теплообменом между ними.

В общем случае тепловой баланс тела характеризуется совместными формами передачи энергетических воздействий.


Уравнение первого закона термодинамики

Рассмотрим взаимодействие среды и рабочего тела. Пусть к телу массой m , объемом V, и температурой Т, расположенному в среде с некоторым давлением р. От среды подводится теплота в количестве dQ. В результате температура увеличится на dT, а объем на dV Рис.2.8.

 

Рис.2.8. К выводу первого закона термодинамики для закрытых систем

В результате увеличения температуры на dT внутренняя кинетическая энергия тела увеличится на dK (возрастает скорость молекулярного и внутримолекулярного движения). Во-первых, увеличение объема тела на dV приводит к изменению взаимного расположения молекул (расстояния между ними), что в результате увеличивает внутреннюю потенциальную энергию тела на dP. Во-вторых с увеличением объема тело совершит работу против внешних сил (внешнее давление) равную dL’.

Для рассматриваемого случая уравнение теплового баланса имеет вид:

или, заменяя через dU – внутренняя энергия тела уравнение примет вид:

Таким образом, каждая термодинамическая система обладает внутренней энергией. Эта функция состояния возрастает на величину подведенной теплоты и убывает на величину совершенной системой внешней работы.

Частные случаи:

- , то , без подвода теплоты от среды работа совершается телом за счет уменьшения его внутренней энергии.

- , то , вся подведенная от среды теплота затрачивается на увеличение внутренней энергии тела.

- , то , вся подведенная теплота от среды, затрачивается на совершение телом работы.

Для удельных величин уравнение примет вид:

Для обратимых процессов работа расширения и внешняя работа равны, а потеря работы на величину кинетической энергии завихрений и трения равна нулю. Для необратимых .Следовательно для классических обратимых процессов уравнение запишем как:

энтальпия

Подставим в уравнение и получим ; обозначим , следовательно: .

Величина i является новой функцией состояния. [Дж/(кг)] – теплосодержание системы, определяемое как сумма внутренней энергии и потенциальной функции .

Физический смысл энтальпии можно выяснить при применении уравнения для процесса при : , или в интегральной форме для обратимых процессов: .

Первое начало термодинамики справедливо как для неподвижных, так и для подвижных систем. При рассмотрении течения рабочего тела в канале произвольной формы, и в частности в газопроводе, уравнение первого закона термодинамики имеет вид:

Рис. 2.9. Графическая интерпретация к выводу первого закона термодинамики для открытых систем.


 

 

Процесс изменения состояния термодинамической системы, характеризуемый изменением ее параметров называется термодинамическим процессом.

Различают равновесное состояние – состояние термодинамической системы, характеризующееся при постоянных внешних условиях неизменностью параметров по времени и отсутствием в системе потоков.

Состояние термодинамической системы не удовлетворяющее данному определению – неравновесное состояние.

В действительности любой реальный процесс является неравновесным, поскольку различные части системы имеют различные значения параметров состояния. Этот факт очень усложняет изучение работы рассматриваемых систем.

В связи с этим, в дальнейшем при анализе термодинамических процессов будем считать, что реальные рассматриваемые процессы представляют собой непрерывную последовательность равновесных состояний (т.е. в сущности, равновесный процесс).

Обратимым принято называть такой процесс, который в условиях изолированной системы, т.е. без внешнего воздействия, допускает возврат системы в исходное состояние. В этом процессе исключены все виды необратимых потерь (трение, диффузия и т.д.), поэтому он наиболее идеализирован.

Переход к реальным (необратимым) процессам обычно осуществляется путем введения в расчеты коэффициентов, характеризующих необратимые потери.

Графическое представление процесса в системе координат p, v называют рабочей диаграммой(для определения работы в процессе). Графическое представление процесса в координатах T, s называют тепловой диаграммой (для определения теплоты в процессе).

Политропный процесс – термодинамический процесс изменения состояния физической системы, в течение которого сохраняется постоянство теплоемкости.

Уравнение политропного процесса имеет вид: .

Давления обратно пропорциональны объемам в степени :

Коэффициент политропы считается для отдельно взятого процесса величиной постоянной значение которой могут изменятся .

При известный параметрах состояния:

Рис.3.1 Сводные диаграммы политропных процессов

 

Работа расширения в политропном процессе:

Используя уравнение состояния и соотношения:

; ; ;,

можно получить приведенные соотношения для работы расширения в адиабатном процессе:

Изменение внутренней энергии в политропном процессе:

При для двух значений температур (и ):

Изменение энтальпии в политропном процессе:

При для двух значений температур (и ):

Количество теплоты в политропном процессе:

При и для двух значений температур (и ):

Изменение энтропии в политропном процессе:

Энтропия в политропном процессе определится по зависимости:

Политропный процесс обобщает всю совокупность основных термодинамических процессов.

Процесс
изохорный
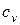
изобарный
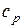
изотермический
адиабатный

 


 

4. Сущность второго закона. Энтропия - параметр состояния, ее физический смысл, изменение в процессах. Общие положения теории циклов. Циклы прямые и обратные. Термический к.п.д, холодильный и отопительный коэффициенты. Цикл Карно.

 

Второй закон (начало) определяет направления реальных (неравновесных процессов): «Невозможен процесс, имеющий единственным своим результатам превращение теплоты в работу».

Исторически открытие второго закона связано с анализом работы тепловых машин и доказательством теоремы от независимости КПД тепловых машин работающих по циклу Карно от вида рабочего тела. Из многолетних наблюдений было установлено, что работа и теплота – неравнозначные формы передачи энергии. Было замечено, что работа может быть полностью превращена в теплоту (трение, электронагрев), теплота не может полностью быть полностью превращена в работу. Такое несоответствие приводит к односторонней направленности реальных процессов происходящих в природе, что отражает физический смысл второго начала термодинамики: «О существовании и возрастании в реальных процессах энтропии», определяющей меру обесценивания энергии.

энтропия – это параметр состояния, изменение которого происходит при обмене энергией в форме теплоты. Энтропию нельзя измерить каким-либо прибором, как и внутреннюю энергию. Принцип существования энтропии используется при анализе обратимых (равновесных) процессов и состоит в утверждении или обосновании существования энтропии как функции состояния. Он гласит: «Для каждой термодинамической системы существует функция состояния (энтропия), изменение которой происходит под действием энергии, подводимой или отводимой в форме теплоты». Для обратимых процессов уравнение запишется в виде:

,[Дж/K)],

Принцип возрастания энтропии используется при анализе необратимых (реальных) процессов. Для необратимых процессов: .

Здесь dQ – элементарное количество теплоты при внешнем теплообмене, dQr – элементарное количество теплоты, обусловленное необратимостью (реальностью) процесса. В любом необратимом процессе величина dQr>0.

Общее уравнение второго закона термодинамики примет вид:

Второй закон термодинамики не позволяет определить меру необратимость (dQr/T), не противоречит закону сохранения энергии, как для обратимых, так и необратимых процессов. Он определяет одностороннюю направленность самопроизвольных необратимых процессов в одностороннем необратимом превращении энергии.

Наиболее популярные формулировки второго закона термодинамики:

«Теплота не может сама собой переходить от холодного тела к горячему» (Р.Клазиус).

«Невозможно создать вечный двигатель второго рода» (В. Оствальд), т.е такую действующую машину которая только бы переводила работу в теплоту, взятую у источника и не нуждалась бы в охладителе более низкой температуры, чем источник теплоты. Таким образом, Энтропия – параметр состояния характеризующая меру необратимости процесса. Следствиями выше приведенных определений являются практические случаи, когда энергия в форме работы самопроизвольно переходит от тел с большим давлением к телам с меньшим давлениям; энергия в форме теплоты самопроизвольно переходит от тел с большей температурой к телам с меньшей температурой.

 

Тепловыми машинами в термодинамике называют тепловые двигатели и холодильные машины.

Тепловой двигатель – непрерывно действующая система, осуществляющая прямые круговые процессы (циклы), в которых теплота превращается в работу.

Прямой термодинамический цикл – цикл, в котором к рабочему телу подводится большее количество теплоты Q1 при большей температуре и отводится меньшее количество теплоты Q2 при более низкой температуре .

Холодильные машины работают по обратному круговому циклу, в котором за счет подводимой извне работы осуществляется перенос теплоты от тел с меньшей температурой к телам с высшей температурой .

Обратный термодинамический цикл – цикл, в котором к рабочему телу подводится меньшее количество теплоты Q2 и при меньшей температуре , а отводится большее количество теплоты Q1 и при более высокой температуре , разность этих теплот равна затраченной работе.

Круговыми процессами (циклами) тепловых машин называют непрерывную последовательность термодинамических процессов, в результате которых, рабочее тело возвращается в исходное состояние.

Следовательно, итоговое изменение любой функции состояния тела в круговом процессе будет равно нулю:

В термодинамической теории круговых процессов рассматриваются лишь элементы внешнего баланса – внешняя работа и внешний теплообмен, следовательно, из первого начала термодинамики по внешнему балансу теплоты и работы получим:

Полученное равенство послужило основанием для использования в теории круговых процессоров термина «превращение теплоты в работу». В действительности ни в одной стадии кругового процесса не происходит прямого и полного превращения теплоты в работу. На Рис. 4.1 приведены произвольные циклы тепловых двигателей (а) и холодильных (б) машин.

 

Рис. 41 Произвольны циклы тепловых машин:

а –цикл теплового двигателя; б –цикл холодильной машины

 

В цикле теплового двигателя (а) от «горячего источника» с температурой отбирается теплота (пл. 1b2de). Холодному источнику с температурой () отдается теплота (пл. 1c2de), а разность этих теплот превращается в полезную работу (пл. 1b2c), которая и передается внешнему потребителю.

Сущность процессов тепловых двигателей заключается в том, что количество теплоты в процессах, расширение и сжатие не равны между собой, при этом работа расширения всегда больше работы затраченной на сжатие.

Качественной характеристикой тепловых двигателей является их термический коэффициент полезного действия , определяемый как отношение получаемой работы к затраченному количеству теплоты :

Термический КПД - характеризует степень совершенства цикла: чем больше его величина, тем большая производится работа при одном и том же количестве подведенной теплоты .

В цикле холодильной машины (б) осуществляется процесс переноса теплоты от «холодного источника» с температурой к источнику высшей температуры , при чем переданная теплота равна сумме отводимой теплоты и работе , подводимой извне.

Качественной характеристикой холодильных машин является холодильный коэффициент , определяемый как отношение количества теплоты, отнимаемой от источника низкой температуры к подведенной извне работе :

Установки, в которых теплота , отдаваемая окружающей среде, является полезным эффектом, называют тепловыми насосами. Эффективность цикла теплового насоса оценивается величиной отопительного коэффициента .

Рабочие диаграммы реальных циклов теплового двигателя и холодильных машин будут отличаться от диаграмм обратимых процессов из-за различия температур рабочего тела и внешнего источника теплоты, а так же за счет наличия необратимых потерь в процессах расширения, сжатия и т.д.

На Рис. 4.2 приведено качественное отличие реальных процессов от идеальных обратимых циклов работы тепловых машин.

 

Рис. 4.2. Относительное расположение обратимых и реальных циклов тепловых машин

а –цикл теплового двигателя; б –цикл холодильной машины

Видно, что диаграмма реального теплового двигателя располагается внутри диаграммы обратимого процесса, а диаграмма холодильной машины – вне диаграммы обратимого цикла. Заштрихованные зоны на диаграммах характеризуют величину необратимых потерь в процессах отвода и подвода теплоты .

Циклы в которых отсутствуют необратимые потери – термодинамические циклы. Несмотря на то, что обратимые циклы практически не осуществимы, их рассмотрение позволяет понять происходящий процесс и приблизить его расчет к реальным условиям работы.

В 1824 году французский физик, инженер Карно Никола Леонард Сади (1796-1832), предложил идеальный обратимый цикл теплового двигателя, состоящий из двух адиабат и двух изотерм. В качестве рабочего тела в цикле используется идеальный газ. На Рис. 4.3 приведен данный цикл в рабочей (а) и тепловой (б) диаграммах.

Рис. 4.3 Цикл Карно для теплового двигателя в р-V (а) и T-S (б) координатах

Для теплового двигателя процесс происходит следующим образом: диаграмма (а).

В процессе 1-2 рабочее тело совершает полезную работу (например, перемещает поршень) из точки 1 в точку 2 при этом температура на участке все время остается неизменной, равной температуре «горячего источника» . Все подведенной тепло идет на работу, связанную с увеличением объема и снижением давления. В точке 2 подвод теплоты к рабочему телу заканчивается, и дальнейшее расширение рабочего тела идет по адиабате 2-3, т.е. при полной тепловой изоляции рабочего тела от внешней среды. При этом температура снижается до температуры «холодного источника» . В точке 3 рабочее тело начинает сжиматься по изотерме 3-4 , при этом температура остается постоянной , за счет отвода теплоты к холодному источнику. В точке 4 отвод теплоты прекращается, и дальнейшее сжатие рабочего тела происходит по адиабате 4-1 с повышением его температуры до . В точке 1 цикл замыкается и далее повторяется тем же образом.

Для холодильных машин, работающих по циклу Карно, расположение процессов аналогично рассмотренному, но направление самих процессов будет противоположно (против часовой стрелки). На тепловой диаграмме цикл Карно представлен в виде прямоугольника, при чем подведенная теплота изображается пл. a12ba. а отведенная теплота пл. a43ba. Следовательно, пл. 1234 характеризует получаемую в цикле работу. Так как рабочим телом является идеальный газ можно записать:

Как было показано, в круговом процессе должно выполняться условие: , следовательно: . С учетом выражения можно записать: ; ; . Следовательно, коэффициенты качественной работы цикла Карно примут вид:

;

Следовательно, в цикле Карно КПД не зависит от характеристики рабочего тела, а зависит только от температуры.