Множественный корелляционно-регрессионный анализ

Тема 4. Множественная регрессия и корреляция

Оценка существенности нелинейной регрессии

Оценивать существенность уравнения нелинейной регрессии будем с помощью средней относительной ошибки аппроксимации:

.

 

 

 

 

Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости переменной у от нескольких объясняющих переменных х₁, х₂, …, х_p, которая может быть решена с помощью множественного корреляционно-регрессионного анализа.

Задачи множественного корреляционно-регрессионного анализа:

1. Измерение тесноты связи между признаками.

2. Отбор факторных признаков в модель.

3. Установление неизвестных причин связи.

4. Определение вида уравнения регрессии.

5. Построение регрессионной модели (уравнения регрессии).

6. Проверка значимости параметров связи.

7. Интервальное оценивание параметров связи.

Модель множественной регрессии – это уравнение, отражающее корреляционную связь между результатом и несколькими факторами. В общем виде оно может быть записано как:

,

где у – зависимая переменная (результат);

х₁, х₂, … х_p – независимые переменные (факторы);

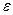- случайный остаток;

f – некая математическая функция.

В качестве функций множественной регрессии часто выбирают наиболее простые – линейную, показательную и степенную функции:

- линейная функция;

 

- показательная функция;

- степенная функция,

где а, b₁, b₂ , … , b_p – параметры уравнения регрессии.

Множественная регрессия широко применяется при исследованиях спроса и потребления, доходности акций, изучении функций издержек и производства и т.д. В настоящее время множественная регрессия – один из наиболее распространенных методов в эконометрике. Его главная цель заключается в построении модели с большим числом факторов и определении при этом влияния каждого из них в отдельности, а так же их совокупности на моделируемый показатель.