Графы пересечений

 

 

Пусть S — множество, а F={S1, ..., Sp} — семейство его различных непустых подмножеств, объединение которых дает S. Граф пересечений семейства F - обозначается W (F) — определяется множеством V(W(F))=F и условием «Si и Sj смежны тогда и только тогда, когда i != j и Si Ç Sj». Граф G называется графом пересечений на множестве S, если существует семейство F подмножеств из S, для которого G=W (F). Сформулируем теперь один из первых результатов о графах пересечений (Марчевский).

Теорема. Любой граф есть граф пересечений.

Доказательство. Для каждой вершины vi графа G — обозначим через Si объединение {vi} и множества ребер, инцидентных vi. Тогда ясно, что G изоморфен графу W (F), где F={Si}.

Определенное выше представление графа приводит еще к одному инварианту. Числом пересечения w(G) данного графа G называется минимальная из мощностей таких множеств S, что G есть граф пересечений на S.

Следствие. Если Gp,q — связный граф и р>= 3 , то w(G)<q.

Доказательство. В этом случае из множеств Si, которые используются в доказательстве теоремы, можно удалить вершины, так что S=X(G).

Следствие. Если Gp,q имеет р0 изолированных вершин, то w(G)<=q+p0

В следующей теореме приводятся условия, при которых достигается эта верхняя оценка.

Теорема. Если Gp,q - связный граф и p> 3, то w(Gp,q) = q тогда и только тогда, когда в Gp,q нет треугольников.

Доказательство. Докажем сначала достаточность. Так как w(Gp,q)<=q (следствие), то остается показать, что w(G_p,q)³q для любого связного графа без треугольников, имеющего, по крайней мере, четыре вершины. Из определения числа пересечения получаем, что G изоморфен графу пересечений W (F) на множестве S, в котором |S| = w(G) элементов. Для каждой вершины vi графа G обозначим через S, соответствующее ей множество. Так как в G нет треугольников, то ни один элемент из S не может встречаться более чем в двух множествах Si и S Ç Sj ¹Æ тогда и только тогда, когда viuj- ребро графа G. Таким образом, мы получаем взаимно однозначное соответствие между ребрами графа G и теми элементами из S, которые принадлежат ровно двум множествам Si. Следовательно, w(G)=|S|>q.

Для доказательства необходимости предположим, что G имеет треугольник. Обозначим через G1 максимальный остовный граф графа G, не имеющий треугольников. Используя доказанную только что достаточность, получаем, что w(G1)=q1= |X(G1)|. Предположим, что G1=W(F), где F - семейство подмножеств некоторого множества S, содержащего q1 элементов. Пусть х - ребро графа G, не принадлежащее G1; рассмотрим граф G2=G1+x. Поскольку Gi- максимальный остовный граф без треугольников, то в G2 должен быть, по крайней мере один треугольник, скажем u1u2u3, где x=u1u3. Обозначим через S1, S2, S3 подмножества в S, соответствующие u1, u2, u3. Если вершина u2 смежна только с u1 и и3 в G1; то заменим S2 на произвольный элемент из S1 Ç S2 и добавим этот элемент к S3. Если u2 смежна ещё с какой-то вершиной, то заменим S3 на объединение S3 и любого элемента из S1 Ç S2. В каждом из возможных случаев приходим к такому семейству F' различных подмножеств множества S, что G2=W (F'). Таким образом, w(G2) = q1, в то время как |X(G2)|=q1+l. Если G2 = G, то доказательство закончено.

Остался случай G2!=G. Обозначим |X(G)| -|X(G2)|=q0. Из предыдущего вытекает, что в этом случае G - граф пересечений на некотором множестве с q1+q0 элементами. Однако q1+q0=q-1. Следовательно, w (G)< q, и теорема доказана.

Число пересечения графа ранее изучалось Эрдёшем, Гудманом и Поша. Они получили наилучшую верхнюю оценку числа пересечения для графов с заданным числом вершин.

Теорема. Для любого графа G с р> 4 вершинами w(G) <[p²/4].

 

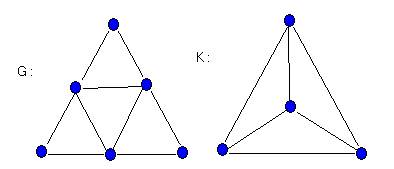
Для произвольного графа G существует граф пересечений, определяемый только полными подграфами графа G. Клика графа — это его любой полный максимальный подграф. Графом клик данного графа G называется граф пересечений семейства всех клик графа G. Например, граф G на рисунке имеет К4 в качестве своего графа клик. Однако неверно, что каждый граф есть граф клик некоторого графа; так, Хамелинк показал, что граф G на рисунке не является графом клик никакого графа. Роберте и Спенсер дали полное описание графов клик:

 

Теорема. Граф G является графом клик тогда и только тогда, когда он содержит семейство F полных подграфов, объединение которых дает G, таких, что если любая пара этих полных подграфов некоторого подсемейства F' имеет непустое "пересечение, то пересечение всех множеств из F' также не пусто.

Замечание. Частный класс графов пересечений был выделен Бензером

при решении задач генетики. Он высказал предположение, что нить генов, представляющую бактериальную хромосому, можно рассматривать как замкнутый интервал на действительной оси. Хайош независимо предположил, что с каждым конечным семейством F интервалов S, можно связать граф, который в терминах графов пересечений есть W(F). Под графом интервалов понимается граф, изоморфный некоторому графу W (F), где F — семейство интервалов. Графы интервалов изучались Боландом и Леккеркеркером , а также Гилмором и Гоффманом .