Прямая в плоскости

ПРЯМАЯ И ПЛОСКОСТЬ

Вплоскости можно провести прямую с различным уклоном, но не превышающим уклон плоскости. Это означает, что интервал любой прямой, лежащей в плоскости, всегда больше интервала ма­сштаба уклона плоскости или равен ему.

Рассмотрим наиболее часто встречающиеся в практике случаи, когда требуется в заданной плоскости провести прямую заданного уклона и, наоборот, через данную прямую провести плоскость с заданным уклоном.

Пусть через точку А,лежащую на горизонтали плоскости Р(рис. 13), требуется провести прямую с заданным уклоном.

Для этого из точки акак из центра проведем окружность с радиусом R,равным интервалу прямой заданного уклона. В пересечении ее ссоседней горизонталью отметим точки типили т₁и п₁.Прямые AMиANлежат в плоскости Ри имеют заданный уклон.

На рис. 14 решена обратная задача: через прямую 5—8про­ведены плоскости Ри Qс заданным уклоном (задача имеет два решения).

Так как горизонтали плоскости с целочисленными отметками должны проходить через точки прямой, имеющие такие же отметки, и проекции этих горизонталей должны быть расположены на расстояниях, равных интервалу масштаба уклона плоскости, то для решения задачи необходимо выполнить следующие построения. Из точки, лежащей на прямой и имеющей целочисленную отметку, например из точки 5как из центра опишем дугу окружности с ради­усом R,равным заданному интервалу масштаба уклона плоскости. Из соседней точки прямой, например точки с отметкой 6,проведем касательные к окружности, которые будут являться горизонталями двух искомых плоскостей Ри Q.

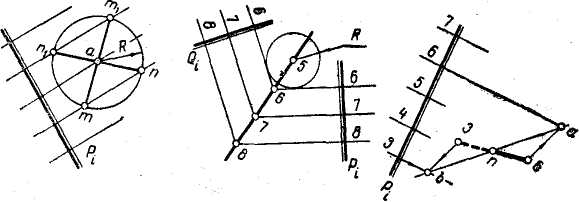
Рис. 13 Рис. 14 Рис. 15