Уклон и интервал прямой

Проекции прямой

Прямая линия может быть задана проекциями двух любых ее точек. Например, прямая, соединяющая проекции а₃и b_{- 4} точек Aи В (рис. 1),является проекцией отрезка АВпрямой линии.

Проекция a₃b_₄с учетом масштаба чертежа вполне определяет положение отрезка прямой в пространстве.*

(*На рис. 1 и на других чертежах, где рассматриваются теоретические основы проекций с числовыми отметками, масштабы как не имеющие в данном случае значения не приводятся).

Уклон прямой определяется тангенсом угла наклона прямой к плоскости уровня и обозначается i.Так, уклон прямой АВ(рис. 2) равен tg а, где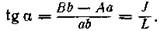

Из этого следует, что уклон прямой равен отношению алгебраической разности отметок концов отрезка к длине его проекции.

Длина проекции abв методе проекций с числовыми отметками называется заложением отрезка прямой и обозначается буквой L.

Разность отметок концов отрезка прямой называется подъе­момотрезка и обозначается буквой J.

Рис. 2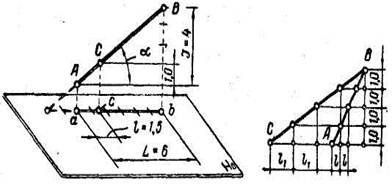Рис. 3

Если разность отметок двух точек прямой равна единице, то заложение отрезка прямой, определяемого этими точками, назы­вается интервалом прямой и обозначается буквой l. Иными словами, интервалом прямой является заложение, соответ­ствующее подъему, равному единице.

Если точка Спрямой АВ (рис. 2) выше точки Ана 1м,то ас = lсоответствует интервалу этой прямой. Как видно из чертежа, интервал l определяется из соотношения

Интервал и уклон прямой линии — величины, обратные друг другу, т.к. уклон прямой равен а интервал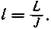

На приведенном чертеже J = 4и L = 6,следовательно, уклон прямой АВ равен

а интервал прямой АВравен:

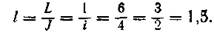
Из вышесказанного следует, что чем больше уклон прямой, тем меньше ее интервал и, наоборот, чем меньше уклон прямой, тем больше ее интервал. Например, уклон прямой АВ(рис. 3) боль­ше, чем уклон прямой СВ,а интервал l прямой АВ меньше интерва­ла l1 прямой СВ.