Лекция 14. Метод последовательных интервалов

 

Содержание лекции: метод последовательных интервалов.

Цели лекции: определение предельно допустимого времени отключения КЗ методом последовательных интервалов.

 

Метод последовательных интервалов позволяет установить предельное время отключения КЗ, учесть действие регуляторов возбуждения, изменение реакции якоря во времени и т.д.

Рассмотрим уравнение движения ротора генератора

 

.

 

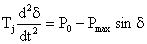Решение этого уравнения в форме δ = f(t) дает картину изменения угла во времени и позволяет установить, остается ли генератор в синхронизме.

Однако это уравнение нелинейно и не может быть решено в общем виде (за исключением частного случая Рmax = 0). Задачу приходится решать методами численного интегрирования уравнений. Одним из них является рассматриваемый метод последовательных интервалов. Для этого весь процесс качания генератора разбивается на ряд небольших интервалов времени Δt и для каждого из этих интервалов последовательно вычисляется приближенное значение приращения Δδ.

В момент КЗ отдаваемая генераторами мощность падает и возникает некоторый избыток мощности ΔР(0). Для достаточно малого интервала времени Δt можно допустить, что избыток мощности в течение этого интервала остается неизменным. Тогда по формулам равномерно ускоренного движения можно определить приращение скорости генератора Δv(1) и угла Δδ(1) в течение первого интервала:

 

; .

 

Относительная скорость машины в момент КЗ равна нулю, и поэтому относительная скорость v(1) в конце первого интервала равна приращению скорости в течение этого интервала, т.е. v(1) = Δ v(1) .

Ускорение α(0) определяется

 

,

следовательно,

 

, (14.1)

здесь угол и время выражены в радианах.

В практических расчетах удобнее пользоваться выражением угла в градусах

 

(14.2)

и времени в секундах

 

. (14.3)

 

Используя (14.2) и (14.3) и принимая во внимание, что , получаем:

 

(14.4)

где угол выражен в градусах, а время и постоянная инерции – в секундах.

Обозначая далее , окончательно получаем:

. (14.5)

 

Зная приращение угла в первом интервале, можно найти абсолютное значение угла в конце этого интервала времени или, что то же самое, в начале следующего интервала: .

Для нового значения угла δ(1) можно определить избыток мощности ΔР(1) во втором интервале времени по формуле

 

.

 

Избыток мощности ΔР(1) создает во втором интервале пропорциональное ему ускорение α(1). При вычислении приращения угла Δδ(2) в течение второго интервала (а также и всех последующих) помимо действующего в этом интервале ускорения α(1) необходимо учесть также уже имеющуюся в начале интервала относительную скорость ротора:

 

. (14.6)

 

Значение скорости v1, получаемой из формулы v(1)= α(0)Δt, является неточным, так как в действительности избыток мощности ΔР(0) и ускорение α(0) не являются постоянными в течение первого интервала времени, а несколько изменяются. Более точные результаты можно получить, если предположить, что ускорение в первом интервале было равно среднему значению

 

.

 

Тогда относительная скорость

 

.

Подставляя это значение в (14.6), находим:

 

или

(14.7)

 

и так далее.

Теперь можно найти угол , определить избыток мощности ΔР(2) и приращение угла Δδ(3):

 

и так далее.

Если в начале некоторого к-го интервала происходит отключение поврежденной цепи, то избыток мощности внезапно изменяется от некоторой величины до величины (см. рисунок 14.1).

 

Рисунок 14.1

 

При вычислении приращения угла в первом интервале после момента отключения значение избытка мощности определяется как среднее из и , т.е.

 

. (14.8)

 

В дальнейших интервалах можно снова пользоваться (14.7). Значение интервала времени Δt при ручном счете принимается обычно равным 0,05 с.

Расчет методом последовательных интервалов ведется до тех пор, пока угол δ не начнет уменьшаться или пока не будет ясным, что угол беспредельно возрастает, т.е. генератор выпадает из синхронизма.

Метод последовательных интервалов можно применять совместно с правилом площадей. Для этого, пользуясь правилом площадей, определяют предельный угол δотк, при котором должно произойти отключение КЗ, и с помощью метода последовательных интервалов определяют время, в течение которого ротор достигает угла δотк. Этот промежуток времени и дает предельное время отключения (см. рисунок 14.2).

 

Рисунок 14.2