Приведение параметров цепи ротора к статору синхронной машины
Такое приведение позволит освободиться от магнитной связи между ротором и статором синхронной машины и представить ее соответствующей схемой замещения.
Для вывода соотношения приведения параметров ротора к статору воспользуемся спрямленной х.х.х. генератора (рис.3.15, б), проходящую через начала координат и точку с координатами ( .
.
При этом получим связи:
 и
и  . (3.41)
. (3.41)
Зная  и
и  , можно построить основной реактивный треугольник, положение вершины которого фиксируется относительным током возбуждения
, можно построить основной реактивный треугольник, положение вершины которого фиксируется относительным током возбуждения  (рис.3.19).
(рис.3.19).

Таким образом, при этом токе возбуждения ток к.з. на выводах генератора будет равен номинально-
му. При этом положение точки  определяется ординатой, представля-
определяется ординатой, представля-
ющей собой относительную величину реактивности  ( так как
( так как  . Точка
. Точка  является проекцией точки
является проекцией точки  на ось тока возбуждения
на ось тока возбуждения  .
.
Ранее установлено, что катет 
Рис.3.19. треугольника  определяет продольную реакцию, создаваемую токами трех фаз статора и тем самым позволяет на графике определить масштаб тока статора
определяет продольную реакцию, создаваемую токами трех фаз статора и тем самым позволяет на графике определить масштаб тока статора  , мм.
, мм.
Таким образом  . (3.42)
. (3.42)
Допустим, что для графика рис.3.19 нами приняты масштабы:
 - для единицы тока возбуждения, мм;
- для единицы тока возбуждения, мм;
 - для единицы э.д.с. статора, мм.
- для единицы э.д.с. статора, мм.
Следовательно, для единицы реактивности можно определить масштаб как  , мм.
, мм.
Выразим ток возбуждения в масштабе тока статора:  .
.
Согласно рис.3.19 можно записать
 ; (3.43)
; (3.43)
 . (3.44)
. (3.44)
Из диаграммы рис.3.19 имеем

 =
= ; или
; или . (3.45)
. (3.45)
В соответствии с принятым спрямлением х.х.х. то есть с учетом (3.41)
 , (3.46)
, (3.46)
то есть истинное и приведенное к статору значения тока возбуждения связаны постоянным (при принятом допущении) коэффициентом пропорциональности, равным  .
.
Для обеспечения обратимости взаимоиндукции между трехфазной обмоткой статора и одноосной обмоткой возбуждения при выражении величин ротора и статора в системе относительных единиц, следует принять на стороне обмотки возбуждения в качестве базисных условий:  , то есть ту же базисную мощность, что и на стороне статора; базисный ток
, то есть ту же базисную мощность, что и на стороне статора; базисный ток  , базисное напряжение
, базисное напряжение  .
.
После того, как все величины цепи обмотки возбуждения будут выражены в относительных единицах при указанных базисных условиях, они одновременно становятся приведенными к статору. Согласованную таким образом систему относительных единиц статора и ротора называют взаимной системой относительных единиц.
3.3.2. Переходные э.д.с. и реактивности синхронной машины
 |
Рассмотрим баланс магнитных потоков в продольной оси ротора синхронной машины в установившемся симметричном режиме ее работы с остающим по фазе током (рис.3.20).
Рис.3.20.
а- холостой ход; б – исходный установившийся режим нагрузки; в – момент внезапного нарушения режима
При отсутствии насыщения мащшины каждый из ее магнитных потоков и их отдельные составляющие можно рассматривать независимо друг от друга.
Рассмотрим баланс магнитных потоков в синхронной машине по продольной оси при разных режимах:
а) при холостом ходе полный магнитный поток обмотки возбуждения  состоит из потока рассеяния
состоит из потока рассеяния  и полезного потока
и полезного потока  , достигающего обмотки статора (рис.3.20.,
, достигающего обмотки статора (рис.3.20.,  );
);
б) при нагруженной машине в установившемся режиме полезный поток 
 является уже геометрической разностью продольного потока в возду-шном зазоре
является уже геометрической разностью продольного потока в возду-шном зазоре  и встречно ему направленного потока реакции статора
и встречно ему направленного потока реакции статора  . Результирующий магнитный поток
. Результирующий магнитный поток  , сцепленный с обмоткой возбуждения равен сумме
, сцепленный с обмоткой возбуждения равен сумме  и
и  (рис.3.20,
(рис.3.20,  );
);
в) при внезапном набросе нагрузки во внешней сети ток статора увеличится и, как следствие, увеличится поток продольной реакции статора на
 . В соответствии с правилом Ленца приращение потока
. В соответствии с правилом Ленца приращение потока  вызовет ответную реакцию обмотки возбуждения
вызовет ответную реакцию обмотки возбуждения  . Исходя из принципа неиз-
. Исходя из принципа неиз-
менности потокосцепления машины в начальный момент переходного про-
цесса, приращения потокосцеплений  и
и  должны компенсиро-
должны компенсиро-
вать друг друга, то есть
 , (3.47)
, (3.47)
или в относительных единицах

 . (3.48)
. (3.48)
Из (3.48) следует, что приращения токов статора  и ротора
и ротора  связаны между собой простым соотношением и различие их обусловлено только реактивностью рассеяния обмотки возбуждения
связаны между собой простым соотношением и различие их обусловлено только реактивностью рассеяния обмотки возбуждения  .
.
В ненасыщенной машине поток  составляет некоторую постоянную долю
составляет некоторую постоянную долю  , которая определяется коэффициентом рассеяния обмотки возбуждения
, которая определяется коэффициентом рассеяния обмотки возбуждения
 . (3.49)
. (3.49)
С увеличением  от
от  до
до  пропорционально ему увеличивается поток рассеяния от
пропорционально ему увеличивается поток рассеяния от  до
до  , что приводит к уменьшению потока
, что приводит к уменьшению потока  до
до  .Однако результирующий поток
.Однако результирующий поток , сцепленный с обмоткой возбуждения, сохраняет свое предшествующее значение
, сцепленный с обмоткой возбуждения, сохраняет свое предшествующее значение  (рис.3.20,
(рис.3.20,  ).
).
Для нахождения э.д.с. статора синхронной машины в начальный момент нарушения режима воспользуемся неизменностью потока , сцепленно-
, сцепленно-
го с обмоткой возбуждения.
Зная коэффициент рассеяния обмотки возбуждения  , определим ту часть магнитного потока
, определим ту часть магнитного потока , которая связана со статором, то есть
, которая связана со статором, то есть
 . (3.50)
. (3.50)
При этом можно утверждать, что потокосцепление (соответствующее магнитному потоку
(соответствующее магнитному потоку  ) и соответствующая ему э.д.с.
) и соответствующая ему э.д.с.  в обмотке стато-
в обмотке стато-
ра сохраняют в начальный момент переходного процесса свои предшеству-
ющие значения.
Раскроем выражение (3.50), опуская индекс ( ):
):
 =
= =
=
 . (3.51)
. (3.51)
Сопоставляя выражения (3.46) и (3.51) и учитывая, что потокосцеплению  соответствует наводимая в обмотке статора э.д.с.
соответствует наводимая в обмотке статора э.д.с.  и все величины выражены в относительных единицах, можно записать:
и все величины выражены в относительных единицах, можно записать:  . (3.52)
. (3.52)
Э.д.с.  называют поперечной переходной э.д.с., а реактивность
называют поперечной переходной э.д.с., а реактивность  -продольной переходной реактивностью, величина которой указывается заводом-изготовителем.
-продольной переходной реактивностью, величина которой указывается заводом-изготовителем.
Покажем рассмотренные величины на векторной диаграмме токов и напряжений явнополюсной синхронной машины для начального момента нарушения режима, работающей с отстающим током (рис.3.21)(опуская индекс “ ”).
”).
 |
Рис.3.21.
Схематично порядок построения может быть таким:
 .
.
Оставаясь неизменной в начальный момент внезапного нарушения режи-
ма, переходная э.д.с. позволяет связать параметры предшествующего ре-
позволяет связать параметры предшествующего ре-
жима с параметрами нового режима (наступившего от внезапного измене-
ния).
В этом и состоит практичекая ценность  . С этой точки зрения термин ”переходная” нужно понимать так, что эта э.д.с. вместе с
. С этой точки зрения термин ”переходная” нужно понимать так, что эта э.д.с. вместе с  позволяет оценить количественно внезапный переход от одного режима к другому. Следует отметить, что э.д.с.
позволяет оценить количественно внезапный переход от одного режима к другому. Следует отметить, что э.д.с.  нельзя измерить (ибо ее значение опреде-
нельзя измерить (ибо ее значение опреде-
ляется по параметрам предшествующего режимa). Поэтому эту э.д.с. нередко называют расчетной или условной.
Придадим выражению  иной вид, введя в него коэффициент рассеяния
иной вид, введя в него коэффициент рассеяния  :
:  . (3.53)
. (3.53)
Из структуры выражения (3.53) непосредственно следует, что реактив-
ность  представляет собой результирующую реактивность статорной обмотки при закороченной обмотке возбуждения (рис.3.22). Причем э.д.с.
представляет собой результирующую реактивность статорной обмотки при закороченной обмотке возбуждения (рис.3.22). Причем э.д.с.
 , соответствующая результирующему потокосцепления обмотки возбуждения
, соответствующая результирующему потокосцепления обмотки возбуждения  S должна быть введена в схему последовательно с
S должна быть введена в схему последовательно с  .
.
После замены ветвей  и
и  одной эквивалентной, получим схему замещения рис.3.22, в, в которой машина представлена своими
одной эквивалентной, получим схему замещения рис.3.22, в, в которой машина представлена своими  и
и  .
.

Рис.3.22.
а-исходная принципиальная схема;
б и в – схемы замещения
В связи с отсутствием у ротора в поперечной оси замкнутых контуров поток поперечной реакции статора  при переходных процессах может изменяться беспрепятственно ( так как отсутствие замкнутых контуров исключает магнитнгое взимодействие). Поэтому внезапное изменение поперечной реакции статора
при переходных процессах может изменяться беспрепятственно ( так как отсутствие замкнутых контуров исключает магнитнгое взимодействие). Поэтому внезапное изменение поперечной реакции статора  (от составляющей
(от составляющей  полного тока стато-
полного тока стато-
ра) учитывают как падение напряженгия от тока  в реактивности
в реактивности  . Таким образом, у такой машины переходная э.д.с. по продольной оси
. Таким образом, у такой машины переходная э.д.с. по продольной оси  , а переходное сопротивление по поперечной оси
, а переходное сопротивление по поперечной оси 
3.3.3. Сверхпереходные э.д.с. и реактивности синхронной машины
Рассмотрим синхронную машину, ротор которой имеет допольнительные (демпферные) короткозамкнутые обмотки на роторе по его обеим осям (рис.3.23).
 Аналогично предыдущему определим э.д.с. и реактивности, которыми можно характеризовать в начальный момент переходного процесса такую машину.
Аналогично предыдущему определим э.д.с. и реактивности, которыми можно характеризовать в начальный момент переходного процесса такую машину.
Заметим, что наличие демпферных обмоток по обеим осям ротора все равно не обеспечивает его магнитную симметрию, что вынуждает определять параметры синхронной машины отдельно в продоль-
Рис.3.23. ной и поперечной осях ротора.
Для простоты анализа примем, что все величины выражены в относительных единицах, величины ротора приведены к статору и обе обмотки ротора в его продольной оси (возбуждения и демпферная) связаны между собой общим потоком взаимоиндукции  , который обусловливает реактивность продольной реакции статора
, который обусловливает реактивность продольной реакции статора  .
.
В такой машине внезапное изменение потока  вызовет ответную реакцию ротора по оси
вызовет ответную реакцию ротора по оси  , которая образуется из приращения магнитного потока обмотки возбуждения
, которая образуется из приращения магнитного потока обмотки возбуждения  и приращения магнитного потока продольной демпферной обмотки
и приращения магнитного потока продольной демпферной обмотки  (здесь 1 указывает номер обмотки, индекс
(здесь 1 указывает номер обмотки, индекс  -расположение по оси
-расположение по оси  ).
).
При внезапном изменении потока  должен сохраниться в начальный момент баланс результирующих потоков (потокосцеплений), сцепленных с обмотками статора, возбуждения и продольной демпферной по оси
должен сохраниться в начальный момент баланс результирующих потоков (потокосцеплений), сцепленных с обмотками статора, возбуждения и продольной демпферной по оси  , то есть должны быть соблюдены следующие равенства:
, то есть должны быть соблюдены следующие равенства:
а) для обмотки возбуждения
 ; (3.54)
; (3.54)
б) для продольной демпферной обмотки
 , (3.55)
, (3.55)
где  ,
,  -приведенный к статору начальный ток, наведенный в продольной демпферной обмотке, и ее реактивность рассеяния.
-приведенный к статору начальный ток, наведенный в продольной демпферной обмотке, и ее реактивность рассеяния.
Приравняв левые части (3.54) и 3.55), получим
 , (3.56)
, (3.56)
откуда видно, что чем меньше рассеяние соответствующей обмотки, тем больше наведенный в ней ток и тем, соответственно, больше ее участие в создании ответной реакции ротора. Также очевидно, что наличие демпфер-
ной обмотки по оси  обусловливает более полную компенсацию продоль-
обусловливает более полную компенсацию продоль-
ного магнитного потока от внезапного приращения потока реакции статора  и частично разгружает обмотку возбуждения в участии ответной реакции.
и частично разгружает обмотку возбуждения в участии ответной реакции.
Заменим совместную ответную реакцию обмотки возбуждения и продоль-
ной демпферной обмотки в начальный момент переходного процесса реакцией от суммарного тока  =
= , протекающего в одной эквивалентной обмотке по продольной оси ротора с реактивностью рассеяния
, протекающего в одной эквивалентной обмотке по продольной оси ротора с реактивностью рассеяния  , то есть
, то есть
 .
.
Далее, используя (3.54) и (3.56), приведем последнее равенство к виду
 ,
,
откуда найдем  . (3.57)
. (3.57)
Таким образом, реактивность рассеяния эквивалентной обмотки в продольной оси ротора можно найти как результирующую реактивность двух параллельных ветвей с  и
и  .
.
Следовательно, для получения реактивности в продольной оси при нали-
чии на роторе одной демпферной обмотки по оси  , характеризующей ма-
, характеризующей ма-
шину в начальный момент внезапного нарушения режима, достаточно в вы-
ражение для  вместо
вместо  ввести выражение для
ввести выражение для  , определив тем самым продольную сверхпереходную реактивность.
, определив тем самым продольную сверхпереходную реактивность.
 . (3.58)
. (3.58)
В поперечной оси ротора, где расположена только одна демпферная обмотка по аналогии с выкладками при определении  можно найти так называемую поперечную сверхпереходную реактивность, характеризую-щую машину в начальный момент внезапного нарушения режима по попе-
можно найти так называемую поперечную сверхпереходную реактивность, характеризую-щую машину в начальный момент внезапного нарушения режима по попе-
речной оси.
 . (3.59)
. (3.59)
Э.д.с. за реактивностями  и
и  называют сверхпереходными э.д.с.
называют сверхпереходными э.д.с.  и
и  , соответственно, в продольной и поперечной осях . Эти э.д.с., как и э.д.с.
, соответственно, в продольной и поперечной осях . Эти э.д.с., как и э.д.с.  , сохраняют свои значения неизменными в начальный момент внезапного нарушения режима. Их величины находят из очевидных равенств:
, сохраняют свои значения неизменными в начальный момент внезапного нарушения режима. Их величины находят из очевидных равенств:  ;
;  . (3.60)
. (3.60)
На рис.3.24 приведена векторная диаграмма токов и напряжений и э.д.с. в начальный момент нарушения режима для явнополюсной синхронной ма-
 |
шины с демпферными обмотками, работающей с отстающим током (опус-
кая индекс “0”).
Рис.3.24.
Схематично порядок построения может быть следующим:
 Как и переходная э.д.с.
Как и переходная э.д.с.  , сверхпереходные э.д.с.
, сверхпереходные э.д.с.  ,
,  и
и  являются расчетными условными величинами.
являются расчетными условными величинами.
Модуль  может быть найден из соотношения
может быть найден из соотношения  .
.
Таким образом, для машины с демпферными обмотками реактивности  и
и вместе с э.д.с.
вместе с э.д.с.  и
и  позволяют перейти от одного режима, изменившегося скачком, к другому. Приставка “сверх” в термине “сверхпереходные” указывает на то, что данные параметры и величины учитывают влияние демпферных обмоток ротора.
позволяют перейти от одного режима, изменившегося скачком, к другому. Приставка “сверх” в термине “сверхпереходные” указывает на то, что данные параметры и величины учитывают влияние демпферных обмоток ротора.
Реактивности  и
и являются характерными параметрами машины и обычно задаются в справочниках.
являются характерными параметрами машины и обычно задаются в справочниках.
Три магнитосязанные обмотки в продольной оси (статора, возбуждения, демпферная) могут быть представлены эквивалентной схемой замещения (рис.3.25,  ), как для трехобмоточного трансформатора. Здесь э.д.с.
), как для трехобмоточного трансформатора. Здесь э.д.с.  и
и  соответствуют результирующим потокосцеплениям обмотки возбуждения и продольной демпферной обмотки. Упрощение этой схемы приводит к
соответствуют результирующим потокосцеплениям обмотки возбуждения и продольной демпферной обмотки. Упрощение этой схемы приводит к  и
и  (рис.3.25,
(рис.3.25, ).
).
В поперечной си ротора, где имеется магнитная связь между обмоткой статора и поперечной демпферной обмоткой (рис.3.26, а), схема замещения будет той же, что и для двухобмоточного трансформатора, после упрощения которой можно получить  и
и  (рис.3.26,
(рис.3.26,  ,
,  ).
).
Полученные схемы замещения машины по осям  и
и  наглядно показывают взаимную связь между приведенными к статору токами отдельных обмоток.
наглядно показывают взаимную связь между приведенными к статору токами отдельных обмоток.
При отсутствии в них активных сопротивлений они отражают только начальный момент переходного процесса.

Рис.3.25.
а- исходная принципиальная схема;
б и в- схемы замещения

Рис.3.26.
а- исходная принципиальная схема;
б и в- схемы замещения
3.3.5. Сравнение э.д.с. и реактивностей синхронной машины
Из схем замещения для реактивностей синхронной машины (рис.3.27) получаем следующие соотношения:
 ;
;  ;
; 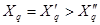 .
.
Попытаемся дополнить и пояснить полученные соотношения из следующих физических соображений.
Магнитный поток, создаваемый током статора 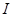 в установившемся режиме, частично замыкается по путям рассеяния статорной обмотки (
в установившемся режиме, частично замыкается по путям рассеяния статорной обмотки ( ), а основная его часть, пройдя через воздушный зазор, замыкается через полюсы и массив ротора (
), а основная его часть, пройдя через воздушный зазор, замыкается через полюсы и массив ротора ( и
и  ). В этих условиях сопротивление для магнитного потока невелико и индуктивности машины, характеризующая величину магнитного потока на единицу намагничивающей сила, максимальны.
). В этих условиях сопротивление для магнитного потока невелико и индуктивности машины, характеризующая величину магнитного потока на единицу намагничивающей сила, максимальны.
При внезапном изменении магнитного потока статора на  в обмотке возбуждения согласно правилу Ленца наводится ток, создающий встречный магнитный поток, который вытесняет магнитный поток статора из тела ротора. Таким образом, при том же возбуждении, что было ранее, при той же намагничивающей силе статора в этих условиях создается меньший магнитный поток, что и обусловливает соответственно меньшую величину переходной реактивности
в обмотке возбуждения согласно правилу Ленца наводится ток, создающий встречный магнитный поток, который вытесняет магнитный поток статора из тела ротора. Таким образом, при том же возбуждении, что было ранее, при той же намагничивающей силе статора в этих условиях создается меньший магнитный поток, что и обусловливает соответственно меньшую величину переходной реактивности  по сравнению с реактивностью
по сравнению с реактивностью  .
.
Очевидно, чем больше будет на роторе замкнутых обмоток, тем меньшая часть магнитного потока статора сможет проникнуть в тело ротора в начальный момент переходного процесса. В пределе, когда весь магнитный поток статора будет вытеснен из тела ротора, реактивность машины в переходном процессе будет минимальной и равной  .
.
Аналогично можно объяснить разницу в реактивностях синхронной машины по поперечной оси.

по продольной оси
по поперечной оси
Рис.3.27.
3.3.5.Характеристики двигателей и нагрузки
Изложенные выше полученные результаты в равной степени относятся как к синхронным генераторам, так и к синхронным двигателям и компенсаторам.
Обратимся теперь к асинхронным двигателям. Проведенный анализ показал [2], что асинхронный двигатель в начале переходного процесса можно рассматривать как невозбужденный синхронный двигатель.
Следовательно, в начальный момент нарушения режима для асинхронно-
го двигателя можно определить сверхпереходные реактивность и э.д.с.
Благодаря полной симметрии ротора, здесь отпадает необходимость разложения величин по отдельным осям.
Сверхпереходная реактивность двигателя может быть получена из его схемы замещения, которая аналогична схеме рис. 3.25, в. Непосредственно из этой схемы замещения следует, что сверхпереходная реактивность асинхронного двигателя  представляет собой реактивность короткого замыкания (то есть когда двигатель заторможен). Относительную величину этой реактивности на практике определяют как
представляет собой реактивность короткого замыкания (то есть когда двигатель заторможен). Относительную величину этой реактивности на практике определяют как
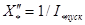 , (3.61)
, (3.61)
где  - относительный пусковой ток двигателя (при пуске без реостата).
- относительный пусковой ток двигателя (при пуске без реостата).
Начальное значение сверхпереходной э.д.с.  двигателя определяют по параметрам предшествующего режима в соответствии с векторной диаграммой рис. 3.28.
двигателя определяют по параметрам предшествующего режима в соответствии с векторной диаграммой рис. 3.28.
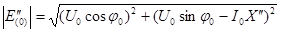 , (3.62)
, (3.62)
или приближенно, если принять э.д.с.  , равной проекции вектора этой э.д.с. на вектор
, равной проекции вектора этой э.д.с. на вектор 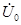
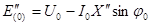 , (3.62, а)
, (3.62, а)
где 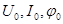 - модули предшествующего напряжения, тока и угла сдвига между их векторами.
- модули предшествующего напряжения, тока и угла сдвига между их векторами.
В практических расчетах начального момента переходного процесса обычно учитывают отдельно лишь крупные двигатели, которые могут оказать существенное влияние на процесс. Все остальные двигатели вместе с другими электроприемниками целесообразно учитывать в виде обобщенных нагрузок
 крупных узлов энергосистемы, характеризуя такие нагрузки средними параметрами.
крупных узлов энергосистемы, характеризуя такие нагрузки средними параметрами.
Установлено, что в начальный момент переходного процесса обобщенную нагрузку можно приближенно характеризовать следующими параметрами: и
и  , считая их выраженными в относительных ...Рис.3.28. единицах при полной рабочей мощности (в МВА) нагрузки и среднем номинальном напряжении той ступени где она присоединена.
, считая их выраженными в относительных ...Рис.3.28. единицах при полной рабочей мощности (в МВА) нагрузки и среднем номинальном напряжении той ступени где она присоединена.

3.3.6. Практический метод расчета
начального сверхпереходного и ударного токов
После определения параметров, которыми характеризуются все элементы электрической системы в момент внезапного нарушения режима вычисление начального сверхпереходного тока не вызывает принципиальных затруднений.
Однако, в практических расчетах с целью упрощения принимают 
 , что позволяет отказаться от разложения величин на составляющие по осям
, что позволяет отказаться от разложения величин на составляющие по осям 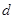 и
и  , а величину сверхпереходной э.д.с. генератора определять по выражениям
, а величину сверхпереходной э.д.с. генератора определять по выражениям
 , (3.63)
, (3.63)
или приближенно
 . (3.63, а)
. (3.63, а)
Такие допущения при определении токов в цепи статора синхронной машины вносят погрешность не более  . Они, конечно, непригодны, если требуется определить токи в цепях ротора.
. Они, конечно, непригодны, если требуется определить токи в цепях ротора.
Таким образом, для расчета  , возникающего при внезапном нарушении режима, следует составить схему замещения, вводя в нее все генераторы, крупные синхронные и асинхронные двигатели, компенсаторы, а также обобщенные нагрузки отдельных мощных узлов энергосистемы своими приведенными к основной ступени напряжения значениями
, возникающего при внезапном нарушении режима, следует составить схему замещения, вводя в нее все генераторы, крупные синхронные и асинхронные двигатели, компенсаторы, а также обобщенные нагрузки отдельных мощных узлов энергосистемы своими приведенными к основной ступени напряжения значениями 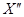 и
и  .
.
Дальнейшее преобразование схемы замещения производится согласно указаниям раздела 2.
В частности, абсолютная величина начального сверхпереходного тока в месте трехфазного к.з. также может быть определена как
 S, (3.64)
S, (3.64)
где 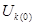 - предшествующее напряжение в месте к.з.;
- предшествующее напряжение в месте к.з.;  - результирующая реактивноcть схемы замещения отноcительно точки к.з.
- результирующая реактивноcть схемы замещения отноcительно точки к.з.
Пуск двигателя по существу можно рассматривать как возникновение к.з. за реактивностью 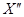 данного двигателя, то есть
данного двигателя, то есть  .
.
На практике при выполнении расчетов начального сверхпереходного тока в месте к.з. обычно учитывают только те обобщенные нагрузки и отдельные
двигатели, которые непосредственно связаны с точкой к.з. или находятся в зоне малой электрической удаленности от нее.
При определении ударного тока обычно учитывают затухание аперидиче-
ской слагающей тока к.з., считая, что амплитуда сверхпереходного тока за полпериода сохраняет свое начальное значение. При этом ударный ток, определяемый для наиболее тяжелых условий, будет

 . О (( (3.65)
. О (( (3.65)
Как известно, ударный коэффициент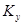 ззавсит от значения постоянной времени цепи к.з.
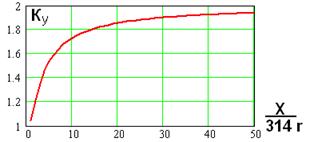
ззавсит от значения постоянной времени цепи к.з. 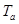 или от отношения ХS/rS. Эта зависимость показана на рис. 3.29.
или от отношения ХS/rS. Эта зависимость показана на рис. 3.29.
С целью упрощения расчетов для разветвленной схемы определяют значение эквивалентной постоянной времени
 ХS/(rSw),
ХS/(rSw),
где ХS - суммарное индуктивное сопротивление схемы замещения, рассчитанное при отсутствии в схеме всех активных сопротивлений;
rS - суммарное активное сопротивление схемы, найденное при отсутствии в ней всех индуктивных сопротивле- ний.
При отдельном учете влияния асинхронных двигателей ударный ток в месте к.з. определяют как  , (3.66)
, (3.66)
где  и
и  -начальный сверхпере-
-начальный сверхпере-
………………Рис.3.29 ходный ток и ударный коэффициент асинхронных двигателей.
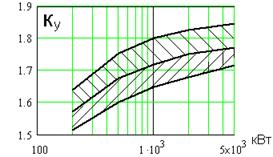 На рис.3.30. представлена зависимость
На рис.3.30. представлена зависимость  от номинальной мощности двигателей, где заштрихованная зона указывает диапазон отклонения этого коэффициента от среднего значения (средняя кривая). Для мелких двигателей (
от номинальной мощности двигателей, где заштрихованная зона указывает диапазон отклонения этого коэффициента от среднего значения (средняя кривая). Для мелких двигателей (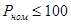 кВт), а также для обобщенной нагрузки практически
кВт), а также для обобщенной нагрузки практически  .
.
У синхронных двигателей величина ударного коэффициента примерно та же, что и у синхронных генераторов равновеликой мощности.
При отсутствии необходимых данных для оценки величины отношения  у отдельных элементов можно ориенти-
у отдельных элементов можно ориенти-
роваться на указанные в таблице Рис.3.30. пределы этого отношения.
Таблица
Значения  для элементов электрической системы
для элементов электрической системы
| Наименование элемента | Отношение 
|
| Турбогенераторы мощностью до 100 МВт | 15-85 |
| То мощностью 100-500 МВт | 100-1400 |
| Гидрогенераторы с демпферными обмотками | 40-60 |
| То же без демпферных обмоток | 60-90 |
| Трансформаторы мощностью 5-30 МВА | 7-17 |
| То же мощностью 60-500 МВА | 20-50 |
| Реакторы 6-10 кВ до 1000А | 15-70 |
| То же 1500 А и выше | 40-80 |
| Воздушные линии | 2-8 |
Кабели 6-10 кВ с медными и алюминиевыми жилами сечением 3х95-3х185
| 0,2-0,8 |
| Обобщенная нагрузка | 2,5 |
В заключение данного параграфа остановимся еще на вопросе несинхрон-
ного включения генератора.
Пусть система, к которой подключается генератор, характеризуется напряжением  и реактивностью
и реактивностью  .
.
Определим, при каких условиях начальное значение сверхпереходного тока при несинхронном включении не превзойдет начального значения сверхпереходного тока генератора при трехфазном к.з. на его выводах. Для этого, очевидно, должно выполняться следующее неравенство:

где 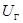 и
и  - напряжение на шинах генератора и угол сдвига вектора этого напряжения относительно вектора напряжения системы;
- напряжение на шинах генератора и угол сдвига вектора этого напряжения относительно вектора напряжения системы;  и
и  -сверхпереходные реактивность и э.д.с. генератора.
-сверхпереходные реактивность и э.д.с. генератора.
При равенстве модулей  поставленное условие будет выполнено, если
поставленное условие будет выполнено, если 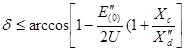 .
.
 |
Эта зависимость при
 представлена на рисунке.
представлена на рисунке.
3.4. УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПЕРЕХОДНОГО ПРОЦЕССА СИНХРОННОЙ МАШИНЫ
3.4.1. Общие замечания и допущения
Аналитическое исследование электромагнитного переходного процесса синхронной машины с учетом всех влияющих на него факторов представля-
ет весьма сложную задачу.
Поэтому для упрощения ее решения вводят ряд допущений:
1. Магнитная система синхронной машины ненасыщенна (индуктивности машины не зависят от величин токов).
2. Распределение кривых н.с. и индукции в воздушном зазоре принимают синусоидальным, соответственно, наведенные в статоре э.д.с. выражаются синусоидами основной частоты.
3. Наличие полной симметрии фазных обмоток статора; ротор симметричен относительно своих осей 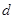 и
и  .
.
4. Предполагается, что все демпферные обмотки на роторе по продольной
оси заменены одной эквивалентной продольной демпферной обмоткой; аналогично, предполагается, что в поперечной оси ротора также имеется только одна эквивалентная поперечная демпферная обмотка.
5.Частота вращения ротора машины в течение всего рассматриваемого переходного процесса постоянна и равна синхронной.
6. В магнитной системе отсутствуют потери.
3.4.2. Исходные уравнения
 |
Принципиальная схема синхронной машины, ротор которой имеет явно выраженные полюсы, представлена на рис.3.31.
Рис.3.31.
На рис.3.31 стрелками указаны принятые положительные направления токов и напряжений в обмотках статора и ротора, а также положительны направления магнитных осей фазных обмоток статора (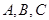 ) и магнитных осей ротора (
) и магнитных осей ротора ( ).
).
Дифференциальные уравнения равновесия э.д.с. и падений напряжения в каждой из обмоток имеют вид:
 ;
;
 (3.67)
(3.67)
где  - индекс фазы для обмотки статора;
- индекс фазы для обмотки статора;
 и
и 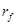 - активные сопротивления, соответственно, контуров каждой фазы статора и цепи возбуждения;
- активные сопротивления, соответственно, контуров каждой фазы статора и цепи возбуждения;
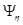 и
и 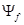 - результирующие потокосцепления соответствующих обмоток, включая их потокосцепления рассеяния.
- результирующие потокосцепления соответствующих обмоток, включая их потокосцепления рассеяния.
Раскроем выражения для потокосцеплений учитывая, что при принятых допущениях они представляют собой линейные зависимости от тока соответствующего контура и токов магнитосвязанных с ним других контуров.
Коэффициентами пропорциональности при этом будут индуктивность  рассматриваемого контура и его взаимоиндуктивности
рассматриваемого контура и его взаимоиндуктивности  с другими контурами.
с другими контурами.
Введя у  и
и  индексы соответствующих обмоток, можно записать:
индексы соответствующих обмоток, можно записать:
 (3.68)
(3.68)
Если бы все  и
и  оставались неизменными при вращении ротора, то система (3.67) состояла бы из линейных дифференциальных уравнений с постоянными коэффициентами. Однако, во вращающейся машине это не имеет место. Кроме индуктивности обмотки возбуждения
оставались неизменными при вращении ротора, то система (3.67) состояла бы из линейных дифференциальных уравнений с постоянными коэффициентами. Однако, во вращающейся машине это не имеет место. Кроме индуктивности обмотки возбуждения  все остальные индуктивности и коэффициенты взаимоиндукции зависят от положения ротора относительно обмоток статора и, следовательно, являются функциями времени.
все остальные индуктивности и коэффициенты взаимоиндукции зависят от положения ротора относительно обмоток статора и, следовательно, являются функциями времени.
В этой связи, систему (3.67) непосредственно решить невозможно, что обусловливает необходимость искать другие (нестандартные) пути решения задачи.
Рассмотрим закономерности изменения индуктивностей обмоток синхронной машины при вращении ротора.
3.4.3. Индуктивности обмоток синхронной машины
Пусть углом  мы будем фиксировать положение ротора: между продольной осью
мы будем фиксировать положение ротора: между продольной осью 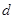 и магнитной осью фазы
и магнитной осью фазы  (рис.3.32).
(рис.3.32).
Синусоидальность наводимых в статоре э.д.с. холостого хода указывает на закон изменения взаимных индуктивностей между обмоткой возбуждения и каждой фазной обмоткой статора.
 Очевидно, он выражается синусои-
Очевидно, он выражается синусои-
дальной функцией с периодом  (для двухполюсной машины это соответст-
(для двухполюсной машины это соответст-
вует одному обороту ротора),максимум которой ( )наступает при совпа-
)наступает при совпа-
дении магнитных осей этих обмоток.
Так, например, для фазы  получим
получим
 . (3.69)
. (3.69)
Изменение индуктивностей фазных обмоток и взаимных индуктивностей между этими обмотками обусловлено
………………Рис.3.32. вращением явнополюсного ротора, при вращении которого непрерывно меняется сопротивление магнитным потокам, определяющие данные индуктивности.
Изменение магнитных потоков происходит гармонически с периодом 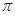 , то есть в два раза меньшим, чем в случае изменения взаимных индуктивностей между обмоткой возбуждения и каждой фазной обмоткой статора (при повороте ротора на угол
, то есть в два раза меньшим, чем в случае изменения взаимных индуктивностей между обмоткой возбуждения и каждой фазной обмоткой статора (при повороте ротора на угол 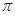 повторяется предыдущий цикл изменения магнитного сопротивления).
повторяется предыдущий цикл изменения магнитного сопротивления).
В практических расчетах ограничиваются приближенными выражениями для этих индуктивностей (при разложении функции в ряд Фурье, изменяющейся по закону косинуса, пренебрегают всеми четными высшими гармониками).
Так индуктивности фаз рассчитывают следующим образом[2]:
 (3.70)
(3.70)
а взаимные индуктивности между обмотками:
 (3.71)
(3.71)
где 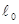 и
и  - постоянные составляющие соответствующих индуктивностей;
- постоянные составляющие соответствующих индуктивностей;
 и
и  - амплитуды вторых гармоник тех же индуктивностей.
- амплитуды вторых гармоник тех же индуктивностей.
В свою очередь, коэффициенты  и
и  выражаются через постоянные индуктивности, которыми характеризуется синхронная машина:
выражаются через постоянные индуктивности, которыми характеризуется синхронная машина:
 (3.72)
(3.72)
3.4.4. Обобщенный вектор трехфазной системы
 |
Вместо представления величин трехфазной системы звездой векторов,проекции которых на ось времени
 дают мгновенные значения этих величин в фазах, можно получить те же мгновенные значения, проектируя единый вектор на три оси времени, каждая из которых сопадает с магнитной осью соответствующей фазы (рис.3.33).
дают мгновенные значения этих величин в фазах, можно получить те же мгновенные значения, проектируя единый вектор на три оси времени, каждая из которых сопадает с магнитной осью соответствующей фазы (рис.3.33).
Рис.3.33.
Такой вектор называют обобщенным вектором трехфазной системы. При его вращении в ту же сторону, что и системы трех векторов, чередование осей времени фаз следует изменить на противоположное.
При симметричном установившемся режиме конец обобщенного вектора описывает с постоянной скоростью окружность, а его величина будет равна амплитуде рассматриваемой величины.
Обобщенным вектором можно характеризовать любые фазные переменные  , изменяющиеся по произвольному закону при соблюдении единственного условия
, изменяющиеся по произвольному закону при соблюдении единственного условия  . (3.73)
. (3.73)
 Модуль искомого обобщенного вектора
Модуль искомого обобщенного вектора 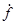 может определен из очевидных равенств (рис.3.34)
может определен из очевидных равенств (рис.3.34)  (3.74)
(3.74)
для чего достаточно их возвести в квадрат и просуммировать:
 ,
,
откуда  (3.75)
(3.75)
Рис.3.34.
Возможность представления трехфазной системы векторов одним обобщенным вектором упрощает выражения связей между статором и ротором, что позволяет в дифференциальных уравнениях переходного процесса синхронной машины освободиться от переменных коэффициентов.
3.4.5. Замена переменных
На рис. 3.34 обобщенный вектор 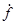 определен в трехосной системе координат ( в фазных осях времени). Тот же вектор можно выразить иначе, например, в двухосной системе координат. Для решения нашей задачи удобно в качестве двухосной системы координат выбрать декартовы ортогональные координаты, жестко связанные с ротором машины. При этом, чтобы ротор был расположен симметрично относительно осей координат, их совмещают соответственно с продольной
определен в трехосной системе координат ( в фазных осях времени). Тот же вектор можно выразить иначе, например, в двухосной системе координат. Для решения нашей задачи удобно в качестве двухосной системы координат выбрать декартовы ортогональные координаты, жестко связанные с ротором машины. При этом, чтобы ротор был расположен симметрично относительно осей координат, их совмещают соответственно с продольной 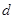 и поперечной
и поперечной  осями ротора.
осями ротора.
Эту систему координат сокращенно называют и обозначают  (рис.3.35).
(рис.3.35).
 Здесь угол
Здесь угол  является функцией времени и отражает вращение ротора с угловой частотой
является функцией времени и отражает вращение ротора с угловой частотой 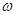 , которая в общем случае может быть переменной.
, которая в общем случае может быть переменной.
Проектируя вектор 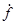 на оси
на оси 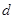 и
и  получим его проекции,
получим его проекции,  (3.76)
(3.76)
связь которых c фазными переменными определяется равенствами:  (3.77) - Рис.3.35.
(3.77) - Рис.3.35.
Решив (3.77) относительно новых переменных, найдем
 (3.78)
(3.78)
До сих пор нами предполагалось, что трехфазная система векторов удовлетворяет условию (3.73). Однако, если сумма фазных переменных (проекции на ось времени  ) не равна нулю, то ее можно выразить через новую переменную
) не равна нулю, то ее можно выразить через новую переменную  , то есть
, то есть
 . (3.79)
. (3.79)
Поскольку составляющая  во всех фазах одинакова, то она не влияет на величину и положение в пространстве обобщенного вектора
во всех фазах одинакова, то она не влияет на величину и положение в пространстве обобщенного вектора 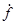 , ни на его составляющие
, ни на его составляющие  и
и 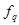 .
.
В этом можно убедиться, подставив в (3.78) вместо  соответственно
соответственно  , которые удовлетворяют условию (3.73).
, которые удовлетворяют условию (3.73).
Таким образом, три переменные в координатах 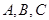 можно однозначно заменить другими тремя переменными в координатах
можно однозначно заменить другими тремя переменными в координатах  При этом в общем случае при переходе к фазным переменным необходимо в каждом из равенств (3.77) прибавить нулевую составляющую, то есть
При этом в общем случае при переходе к фазным переменным необходимо в каждом из равенств (3.77) прибавить нулевую составляющую, то есть
 (3.80)
(3.80)
Переход от трехосной (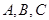 ) к двухосной системе координат (
) к двухосной системе координат (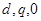 ) соответствует тому, что трехфазная машина по существу заменена эквивалентной двухфазной.
) соответствует тому, что трехфазная машина по существу заменена эквивалентной двухфазной.
Именно по этой причине целесообразно перейти от переменных в координатах 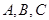 к переменным в координатах
к переменным в координатах 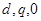 . Такой переход позвляет уравнения (3.67) преобразовать в дифференциальные уравнения с постоянными коэффициентами.
. Такой переход позвляет уравнения (3.67) преобразовать в дифференциальные уравнения с постоянными коэффициентами.
Рассмотренное выше преобразование впервые было предложено Блонделем для установившегося режима явнополюсной синхронной машины и впоследствии было развито Парком и Горевым для условий переходного процесса.
3.4.6. Преобразование уравнений
Применим полученные результаты для преобразования исходных дифференциальных уравнений (3.67). В соответствии с (3.80) выразим ток, напряжение и потокосцепление фазы  через новые переменные:
через новые переменные:
 (3.81)
(3.81)
Подставим их в первое уравнение (3.67), имея в виду, что  и
и  являются функциями времени
являются функциями времени  После подстановки получим:
После подстановки получим:

Сгруппируем слагаемые относительно  и
и 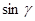 , получим
, получим
 . (3.82)
. (3.82)
Уравнение (3.82) должно быть удовлетворено при любых значениях угла  , что возможно только при условии, что каждое из выражений, заключенных в скобки, тождественно равно нулю.Таким образом, уравнение (3.82) (для фазы
, что возможно только при условии, что каждое из выражений, заключенных в скобки, тождественно равно нулю.Таким образом, уравнение (3.82) (для фазы  ) распадается на три уравнения
) распадается на три уравнения

 (3.83)
(3.83)
 (3.84)
(3.84)

 (3.85)
(3.85)
При записи (3.83)-(3.85) в относительных единицах потокосцепления можно представить в следующем виде
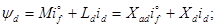 (3.86)
(3.86)
 (3.87)
(3.87)
 (3.88)
(3.88)
где  -реактивность и индуктивность нулевой последовательности машины.
-реактивность и индуктивность нулевой последовательности машины.
Отметим еще раз, что в (3.82)-(3.86) токи 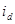 и
и  представляют собой проекции обобщенного вектора тока статора
представляют собой проекции обобщенного вектора тока статора  на оси
на оси 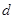 и
и  .
.
Таким образом, переход к новым переменным в координатах 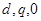 позволил преобразовать систему (3.67) в уравнения (3.82)-(3.86), где все коэффициенты постоянные величины.
позволил преобразовать систему (3.67) в уравнения (3.82)-(3.86), где все коэффициенты постоянные величины.
Уравнения (3.83)-(3.85) выражают основу теории двух реакции синхронной машины при электромагнитном переходном процессе. Эти уравнения называют уравнениями Парка-Горева.
Если изменения угла  , характеризующие движение ротора, выразить соответствующим уравнением, то вместе с ранее составленными уравнениями для цепей ротора и статора получим систему уравнений, которая будет отражать одновременное протекание электромагнитного и электромеханического переходного процессов с учетом их взаимного влияния.
, характеризующие движение ротора, выразить соответствующим уравнением, то вместе с ранее составленными уравнениями для цепей ротора и статора получим систему уравнений, которая будет отражать одновременное протекание электромагнитного и электромеханического переходного процессов с учетом их взаимного влияния.
Для анализа только электромагнитного переходного процесса в соответствии с допущением 5 в дальнейшем будем считать
 ,
,
где  - синхронная угловая частота;
- синхронная угловая частота;  - начальный угол.
- начальный угол.
Следовательно, в этом случае  и в относительных единицах при
и в относительных единицах при  получим
получим  . (3.89)
. (3.89)
Тогда уравнения (3.83)-(3.85) для фазы  будут иметь вид
будут иметь вид
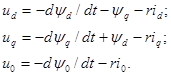 (3.90)
(3.90)
В заключение отметим, что в (3.83) и (3.84) первые слагаемые представляют собой э.д.с. трансформации, поскольку они обусловлены изменением величин соответствующих потокосцеплений, а вторые слагаемые –э.д.с. вращения. В стационарном режиме трансформаторные э.д.с., естественно, отсутствуют.
3.4.7. Выражения в операторной форме
Известно, что анализ дrtBefore(gcse, s);
})();