Основы булевой алгебры
Шестнадцатеричная система счисления
Основание этой системы счисления p равно шестнадцати. В качестве цифр в шестнадцатеричной системе используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Так как здесь появляются новые цифры, то приведём таблицу соответствия этих цифр десятичным значениям.
Таблица 6. Таблица соответствия шестнадцатеричных цифр десятичным значениям
| Шестнадцатеричная цифра | Десятичный эквивалент |
| A | |
| B | |
| C | |
| D | |
| E | |
| F |
Рассмотрим пример записи шестнадцатеричного числа:
A16=2AF,C416=2*162+10*161+15*160+12*16-1
+4*16 -2=
=51210+16010+1510+1210/1610+410/25410= 687,76562510
Из приведённых примеров записи чисел в различных системах счисления вполне очевидно, что для записи одного и того же числа с одинаковой точностью в разных системах счисления требуется различное количество разрядов. Чем больше основание системы счисления, тем меньшее количество разрядов требуется для записи одного и того же числа.
Основными понятиями булевой алгебры являются понятия логической переменной и логической функции.
Логической переменной называется величина, которая может принимать одно из двух возможных состояний (значений), одно из которых обозначается символом “0”, другое – “1” (для обозначения состояний возможно применение и других символов, например, “Да” и “Нет” и др.).
Сами двоичные переменные чаще обозначают символами х1, х2,… В силу определения логические переменные можно называть также двоичными переменными.
Логической (булевой) функцией (обычное обозначение – у) называется функция двоичных переменных (аргументов), которая также может принимать одно из двух возможных состояний (значений): “0” или “1”.
Значение некоторой логической функции n переменных определяется или задается для каждого набора (сочетания) двоичных переменных. Количество возможных различных наборов, которые могут быть составлены из n аргументов, очевидно, равно 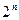 . При этом, поскольку сама функция на каждом наборе может принимать значение “0” или “1”, то общее число возможных функций от n переменных равно
. При этом, поскольку сама функция на каждом наборе может принимать значение “0” или “1”, то общее число возможных функций от n переменных равно  .
.
Таким образом, множество состояний (значений), которые могут принимать как аргументы, так и функции, равно двум.
Для этих состояний в булевой алгебре определяются отношение эквивалентности,
обозначаемое символом равенства (=)
и три операции:
а) логического сложения (дизъюнкции),
б) логического умножения (конъюнкции),
в) логического отрицания (инверсии), обозначаемые соответственно символами:
+ или  - операция дизъюнкции,
- операция дизъюнкции,
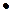 или
или  или & - операция конъюнкции,
или & - операция конъюнкции,
 - операция инверсии (* - символ аргумента или функции).
- операция инверсии (* - символ аргумента или функции).
Постулативно полагается, что при выполнении перечисленных операций отношения эквивалентности имеют вид:
а) 0 + 0 = 0,
б) 0 × 0 = 0,
в) = 1,
= 1,

0 + 1 = 1,
0 × 1 = 0, 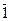 = 0.
= 0.
1 + 0 = 1, 1 × 0 = 0,
1 + 1 = 1; 1 × 1 = 1;
На основании постулатов (1) можно вывести следующие соотношения (законы) алгебры логики:
1. Законы одинарных элементов (универсального множества – а), нулевого множества – б), тавтологии – в)):
 а) х + 1 = 1,
а) х + 1 = 1,
б) х + 0 = х,
в) х + х = х,
х × 1 = х; х × 0 = 0; х × х = х.
2. Законы отрицания (двойного отрицания – а), дополнительности – б), двойственности – в)):
 а)
а) 
б) 
в) 
 ;
;  .
.
3. Законы абсорбции или поглощения – а) и склеивания – б):
 а)
а) 
б) 
в) 

Законы двойственности (3, в), называемые также законами деМоргана,
Кроме законов, перечисленных выше и не имеющих аналогов в обычной алгебре (алгебре чисел), для алгебры логики справедливы законы обычной алгебры: коммутативные или переместительные, дистрибутивные или распределительные, ассоциативные или сочетательные.
Любая логическая функция у n двоичных переменных  может быть задана таблично. Такие таблицы, получившие название таблиц истинности, содержат
может быть задана таблично. Такие таблицы, получившие название таблиц истинности, содержат 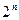 строк, в которые записываются все возможные двоичные наборы значений аргументов, а также соответствующее каждому из этих наборов значение функции.
строк, в которые записываются все возможные двоичные наборы значений аргументов, а также соответствующее каждому из этих наборов значение функции.
Алгебра логики предполагает возможность образования сложных функций, т.е. функций, аргументы которых являются функциями других двоичных аргументов. Например, если  , а
, а  и
и  , очевидно, что
, очевидно, что  . Операция замены аргументов одной функции другими функциями называется суперпозицией функций. Эта операция дает возможность выразить сложную логическую функцию через более простые (элементарные).
. Операция замены аргументов одной функции другими функциями называется суперпозицией функций. Эта операция дает возможность выразить сложную логическую функцию через более простые (элементарные).
Приведем описание некоторых, имеющих большое значение в цифровой технике, элементарных логических функций и ЛЭ, реализующих эти функции.
Логические элементы или, как их еще называют, вентили (по-английски gates) — это наиболее простые цифровые микросхемы. Именно в простоте и состоит их отличие от других микросхем. Как правило, в одном корпусе микросхемы может располагаться от одного до шести одинаковых логических элементов. Иногда в одном корпусе могут располагаться и разные логические элементы.
Обычно каждый логический элемент имеет несколько входов (от одного до двенадцати) и один выход. При этом связь между выходным сигналом и входными сигналами (таблица истинности) предельно проста. Каждой комбинации входных сигналов элемента соответствует уровень нуля или единицы на его выходе.
Никакой внутренней памяти у логических элементов нет, поэтому они относятся к группе так называемых комбинационных микросхем. Но в отличие от более сложных комбинационных микросхем логические элементы имеют входы, которые не могут быть разделены на группы, различающиеся по выполняемым ими функциям.
Самый простой логический элемент — это инвертор (логический элемент НЕ, англ. inverter), который выполняет простейшую логическую функцию — инвертирование, т. е. изменение уровня входного сигнала на противоположный (см. рис. 1). Инвертор имеет всего один вход и один выход(табл. 1).
1. Таблица истинности инвертора
| Вход | Выход |
Следующий шаг на пути усложнения компонентов цифровой электроники — это элементы, выполняющие простейшие логические функции. Объединяет все эти элементы то, что у них есть несколько равноправных входов (от 2 до 12) и один выход, сигнал на котором определяется комбинацией входных сигналов.
Самые распространенные логические функции — это И
(в отечественной системе обозначений — ЛИ), И-НЕ (обозначается ЛА), ИЛИ (обозначается ЛЛ) и ИЛИ-НЕ (обозначается ЛН). Присутствие слова НЕ в названии элемента обозначает только одно — встроенную инверсию сигнала.
В международной системе обозначений используются следующие сокращения: AND — функция И, NAND — функция И-НЕ, OR — функция ИЛИ, NOR — функция ИЛИ-НЕ.
Элемент И формирует на выходе единицу тогда и только
тогда, если на всех его входах (и на первом, и на втором, и на третьем и т. д.) присутствуют единицы.
Если речь идет об элементе И-НЕ, то на выходе формируется нуль, когда на всех входах — единицы (табл. 2). Присутствие слова НЕ в названии элемента обозначает только одно — встроенную инверсию сигнала.
Элемент ИЛИ формирует на выходе нуль тогда и только
тогда, если на всех входах нуль. Элемент ИЛИ-НЕ дает на
выходе нуль при наличии хотя бы на одном из входов единицы.
2. Таблица истинности двухвходовых
элементов
И, И-НЕ, ИЛИ, ИЛИ-НЕ
| Вход 1 | Вход 2 | Выход И | Выход И-НЕ | Выход ИЛИ | Выход ИЛИ-НЕ |
Отечественные и зарубежные обозначения на схемах двухвходовых элементов И, И-НЕ, ИЛИ, ИЛИ-НЕ показаны на рис. 2.
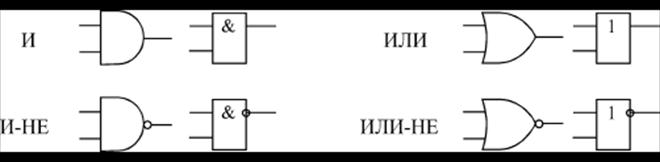
Рис. 2. Обозначения элементов И, И-НЕ, ИЛИ, ИЛИ-НЕ:
зарубежные (слева) и отечественные (справа)
Элементы «Исключающее ИЛИ» (по-английски Exclusive-OR) также можно было бы отнести к простейшим элементам, но функция, выполняемая ими, несколько сложнее, чем в случае элемента И или элемента ИЛИ.
Все входы элементов «Исключающее ИЛИ» равноправны, однако ни один из входов не может заблокировать другие входы, установив выходной сигнал в уровень единицы или нуля.
Под функцией «Исключающее ИЛИ» понимается следующее: единица на выходе появляется тогда, когда только на одном входе присутствует единица (рис. 3).
Надпись на отечественном обозначении элемента «Исключающее ИЛИ» =1 как раз и обозначает, что выделяется ситуация, когда на входах одна и только одна единица.

Рис. 3. Обозначения элементов «Исключающее ИЛИ»:
зарубежные (слева) и отечественные (справа)
Если единиц на входах две или больше, или если на всех входах нули, то на выходе будет нуль (табл. 3).
3. Таблица истинности «Исключающее ИЛИ»
| Вход 1 | Вход 2 | Вход 3 |