Парная корреляция

Наиболее разработанной в теории статистики является методология однофакторного корреляционно-регрессионного анализа или парной корреляции, рассматривающей влияние вариации факторного признака x на результативный y.

Важнейшим этапом построения регрессионной модели (уравнения регрессии) является установление на основе анализа исходной информации соответствующей математической функции. Сложность заключается а том, что из множества функций необходимо найти такую, которая лучше других выражает реально существующие связи между анализируемыми признаками. Выбор типа функции может опираться на теоретические знания об изучаемом явлении, опыт предыдущих аналогичных исследований или осуществляется эмпирическим перебором и оценкой функций различных типов.

При изучении связи экономических показателей используют различные виды уравнения прямолинейной и криволинейных связей, внимание к линейным связям обеспечивается тем, что в большинстве случаев нелинейные формы для выполнения расчетов путем логарифмирования или замены переменных могут быть преобразованы в линейную форму.

Уравнение парной линейной корреляции имеет вид (9.1):

Где - теоретические значения результативного признака, получен­ные по уравнению регрессии;

- коэффициенты (параметры) уравнения регрессии.

Поскольку является средним значением y в точке x=0, его экономическая интерпретация часто затруднена или вообще невоз­можна.

Коэффициент парной линейной регрессииa₁ имеет смысл показателя силы связи между вариацией факторного признака x и вариацией результативного признака. Коэффициент показывает среднее значение изменения результативного признака y при изменении факторного признака x на одну единицу его измерения, т.е. вариацию y, приходящуюся на единицу вариации x. Знак a₁ указывает направление этого изменения.

Параметры уравнения a₀, a₁ находятся методом наименьших квадратов, в основу которого положено требование минимальности сумм квадратов отклонений эмпирических данных y₁ от теоретических (9.2):

Для нахождения минимума данной функции ее частные производные приравниваются к нулю и решается следующая система нор­мальных уравнений (9.3):

Решение системы позволяет определить параметры уравнения регрессии. В общем виде параметры определяются следующим образом (9.4):

Параметры уравнения регрессии в ряде случаев удобно вычис­лять по следующим формулам, дающим тот же результат (9.5) и (9.6):

Рассчитанные таким образом значения a₀ и a₁ подставляются в уравнения регрессии.

Для практического использования моделей регрессии большое значение имеет их адекватность, т. е. соответствие фактическим ста­тистическим данным. Корреляционный и регрессионный анализ за­частую проводится для небольшой по объему совокупности. Поэтому показатели регрессии и корреляции могут быть искажены действием случайных факторов, и требуется проверка адекватности модели.

При численности объектов анализа до 30 единиц возникает не­обходимость проверки значимости (существенности) каждого коэф­фициента регрессии. При этом выясняют, насколько вычисленные па­раметры x характерны для отображения комплекса условий: не явля­ются ли полученные значения параметров результатом, действия слу­чайных причин.

Значимость коэффициентов простой линейной регрессии (при­менительно к совокупностям, у которых n<30) осуществляют с помо­щью t-критерия. При этом вычисляют расчетные (фактические) значе­ния t-критерия:

для параметра a₀ (9.7):

 

для параметра a₁ (9.8):

 

где n – объем выборки;

- среднее квадратическое отклонение фактических значений результативного признака y от теоретических значений (9.9),

 

- среднее квадратическое отклонение значений факторного признака x от общей средней (9.10):

Вычисленные значения сравнивают с критическими t_табл. , которые определяют по таблице Стьюдента с учетом принятого уров­ня значимости a и числа степеней свободы вариации V=n-K-1, К - число факторных признаков в уравнении.

В социально-экономическихисследованиях уровень значимостиa обычно принимают равным 0,05. Параметр признается значимым (существенным) при условии, если . В таком случае практически невероятно, что найденные значения параметров обусловленытолько случайными совпадениями.

Проверка адекватности регрессионной модели может быть дополнена корреляционным анализом. Для этого необходимо определитьтесноту корреляционной связи между переменными x и y. Тесно-корреляционной связи, как и любой другой, может быть измерена эмпирическим корреляционным отношением (9.11):

Где – межгрупповая дисперсия результативного признака, характеризующая отклонение групповых средних этого признака от общей средней.

Говоря о корреляционном отношении как о показателе измерения тесноты зависимости от эмпирического корреляционного отношения следует отличать теоретическое. Теоретическое корреляционное отношениепредставляет собой относительную величину, получающуюся в результате сравнения среднего квадратического отклонения теоретических значений результативного признака (рас­считанных по уравнению регрессии) со средним квадратическим отклонением эмпирических (фактических) значений результативного признака (9.12), (9.13), (9.14), (9.15):

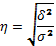
Где

Тогда представляет собой коэффициент детерминации, ко­торый показывает долю вариации результативного признака под влиянием вариации признака-фактора.

Теоретическое корреляционное отношение применяется для изме­рения тесноты связи при линейной и криволинейной зависимостях стях между результативным и факторным признаками. Теоретическое кор­реляционное отношение часто называют индексом корреляции R. Корреляционное отношение может находиться в пределах от 0 до 1, т. е. ). Чем ближе корреляционное отношение к 1, тем сильнее связь между признаками.

Отметим, что при линейной форме уравнения применяется другой показатель тесноты связи - линейный коэффициент корреляции (9.16):

Где n – число наблюдений.

Для практических вычислений при малом числе наблюдений линейный коэффициент корреляции удобнее вычислять по формуле (9.17):

Значение линейного коэффициента корреляции важно для исследования социально-экономических явлений и процессов, распределение которых близко к нормальному и принимает значение в интервале (9.18):

Отрицательные значения указывают на обратную связь, положительные – на прямую. При r=0 линейная связь отсутствует. Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее линейная связь между признаками. При связь линейная функциональная.

Квадрат линейного коэффициента корреляции r² называется линейным коэффициентом детерминации. При оценке степени тес­ноты связи он полностью соответствует теоретическому корреляционному отношению, которое является более универсальным показате­лем тесноты связи по сравнению с линейным коэффициентом корре­ляции. Факт совпадений значений теоретического корреляционного отношения 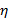и линейного коэффициента корреляции r используется для оценки формы связи значения - η и r совпадают только при нали­чии прямолинейной связи.

Несовпадение этих величин свидетельствует, что связь между изучаемыми признаками криволинейная. Установлено, что если разность квадратов η² и r² не превышает 0,1, то гипотезу о прямолинейной форме связи можно считать подтвержденной.

Показатели тесноты связи, исчисленные по данным сравнитель­но небольшой статистической совокупности, могут искажаться дейст­вием случайных величин. Это вызывает необходимость проверки их существенности.

Для оценки значимости коэффициента корреляции r используют t-критерий Стьюдента, который применяется при t-распределении, отличном от нормального.

При линейной однофакторной связи t-критерий можно рассчи­тать по формуле (9.19):

 

 

гле (n-2) — число степеней свободы при заданном уровне значимости a и объеме выборки n.

Полученное значение t_расч сравнивают с табличным значением t-критерия (для a=0,05 и 0,01). Если рассчитанное значение превос­ходит табличное значение критерия t_табл , то практически невероятно, что найденное значение обусловлено только случайными колебания­ми, т. е. гипотеза о случайности отвергается.

После проверки адекватности построенной модели (уравнение регрессии) ее необходимо проанализировать, дать экономическую ин­терпретацию параметров регрессии. Прежде всего нужно проверить, согласуются ли знаки параметров с теоретическими представлениями и соображениями о направлении влияния признака-фактора на резуль­тативный признак. Далее необходимо проанализировать значение па­раметра a₁. Очевидно, что для линейной регрессии параметр a₁ говорит о том, на сколько абсолютных единиц изменится результативный признак при изменении факторного на 1. Для удобства интерпретации параметра a₁ используют коэффициент эластичности. Он показыва­ет, на сколько процентов от его среднего значения изменится результативный признак при изменении факторного признака на 1% от его средней величины, и вычисляется по формуле (9.20):

Далее имеет смысл вычислить остатки , характери­зующие отклонение i-х наблюдений от значений, которые следует ожидать в среднем (т. е. в соответствии с уравнением регрессии). Наибольший интерес будут представлять наблюдения с наибольшими положительным и отрицательным остатками.

Пример. Методами корреляционного и регрессионного анализа требуется оценить зависимость производительности труда рабочих от стажа их работы по следующим исходным данным.