Тогда с учетом обозначений (2.13, 2.14) выражение (2.12) принимает вид
Рис. 2.7. Виды нелинейных функций
Рис. 2.6. Виды линейной функции
Рис. 2.5. Виды статических характеристик
Рис. 2.3. Переходные и установившиеся режимы при типовых воздействиях
Рис. 2.2. Виды типовых воздействий
Коэффициент а1 характеризует скорость нарастания воздействия x(t).
По характеру изменения выходной величины во времениразличают следующие режимы элемента АСУ:
· статический;
· динамический.
Статический режим – состояние элемента АСУ, при котором выходная величина не изменяется во времени, т. е. y(t) = const.
Очевидно, что статический режим (или состояние равновесия) может иметь место лишь тогда, когда входные воздействия постоянны во времени. Связь между входными и выходными величинами в статическом режиме описывают алгебраическими уравнениями.
Динамический режим – состояние элемента АСУ, при котором входная величина непрерывно изменяется во времени, т. е. y(t) = var.
Динамический режим имеет место, когда в элементе после приложения входного воздействия происходят процессы установления заданного состояния или заданного изменения выходной величины. Эти процессы описываются в общем случае дифференциальными уравнениями.
Динамические режимы в свою очередь разделяются на:
· неустановившийся (переходный);
· установившийся (квазиустановившийся).
Неустановившийся (переходный) режим – режим, существующий от момента начала изменения входного воздействия до момента, когда выходная величина начинает изменяться по закону этого воздействия.
Установившийся режим – режим, наступающий после того, когда выходная величина начинает изменяться по такому же закону, что и входное воздействие, т. е. наступающий после окончания переходного процесса.
В установившемся режиме элемент совершает вынужденное движение. Очевидно, что статический режим является частным случаем установившегося (вынужденного) режима при x(t) = const.
Понятия «переходный режим» и «установившийся режим» иллюстрируются графиками изменения выходной величины y(t) при двух типовых входных воздействиях x(t) (рис. 2.3). Граница между переходным и установившимся режимами показана вертикальной пунктирной линией.
2.3. Статические характеристики элементов
Передаточные свойства элементов и АСУ в статическом режиме описывают с помощью статических характеристик.
Статическая характеристика элемента – зависимость выходной величины y элемента от входной x
y = f(x) = y(x) (2.10)
в установившемся статическом режиме.
Статическая характеристика конкретного элемента может быть задана в аналитическом виде (например, y = kx2) или в виде графика (рис. 2.4).
Рис. 2.4. Статическая характеристика элемента
Как правило, связь между входной и выходной величинами – однозначная. Элемент с такой связью называют статическим (позиционным) (рис. 2.5, а). Элемент с неоднозначной связью – астатическим (рис. 2.5, б).
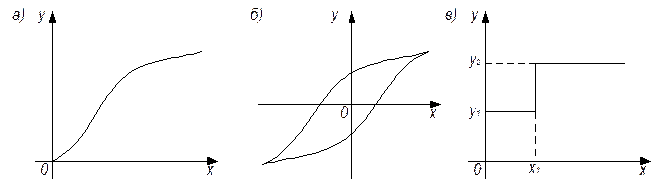
По виду статических характеристик элементы разделяют на:
· линейные;
· нелинейные.
Линейный элемент – элемент, имеющий статическую характеристику в виде линейной функции (рис. 2.6):
y = b + ax. (2.11)
 |
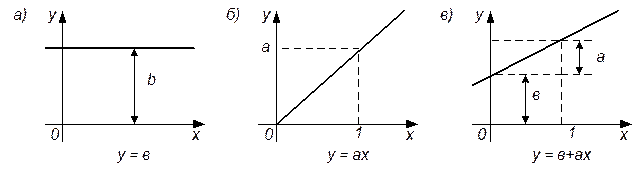Нелинейный элемент – элемент, имеющий нелинейную статическую характеристику.
Нелинейная статическая характеристика аналитически обычно выражается в виде степенных функций, степенных полиномов, дробных рациональных функций и более сложных функций (рис. 2.7).
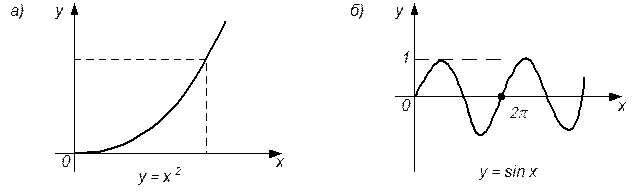
Нелинейные элементы в свою очередь подразделяют на:
· элементы с существенно нелинейной статической характеристикой;
· элементы с несущественно нелинейной статической характеристикой;
Несущественно нелинейная статическая характеристика – характеристика, описываемая непрерывной дифференцируемой функцией.
Практически это математическое условие означает, что график функции y = f(x) должен иметь гладкую форму (рис. 2.5, а).В ограниченном диапазоне изменения входной величины x такая характеристика может быть приближенно заменена (аппроксимирована) линейной функцией. Приближенная замена нелинейной функции линейной называется линеаризацией. Линеаризация нелинейной характеристики правомерна, если в процессе работы элемента его входная величина меняется в небольшом диапазоне вокруг некоторого значения x = x0 .
Существенно нелинейная статическая характеристика – характеристика, описываемая функцией, имеющей изломы или разрывы.
Примером существенно нелинейной статической характеристики может служить характеристика реле (рис. 2.5, в), которое при достижении входного сигнала x (ток в обмотке реле) некоторого значения x1изменит выходной сигнал y (напряжение в коммутируемой цепи) с уровня y1 до уровня y2 . Замена такой характеристики прямой линией с постоянным углом наклона привела бы к существенному несоответствию между математическим описанием элемента и реальным физическим процессом, протекающем в элементе. Поэтому существенно нелинейная статическая характеристика линеаризации не подлежит.
Линеаризацию гладких (несущественно нелинейных) статических характеристик можно осуществлять либо по методу касательной, либо по методу секущей.
Так, например, линеаризация по методу касательной заключается в разложении функции y(x) в интервале вокруг некоторой точки x0 в ряд Тейлора и в последующем учете первых двух членов этого ряда:
y(x) » y(x0) + y¢(x0)(x – x0), (2.12) где y¢(x0) – значение производной функции y(x) в заданной точке А с координатами x0 и y0 .
 |
Геометрический смысл такой линеаризации заключается в замене кривой y(x) касательной ВС, проведенной к кривой в точке А (рис. 2.8).
Рис. 2.8. Линеаризация статической характеристики методом касательной
При анализе АСУ удобно линейные статические характеристики рассматривать в отклонениях переменных x и y от значений x0 и y0 :
Dy = y - y0 ; (2.13)
Dx = x - x0 . (2.14)
Dy = k Dx, (2.15)
где k = y¢(x0) – передаточный коэффициент элемента, характеризующий его передаточные свойства в статическом режиме.
2.4. Динамические характеристики элементов АСУ
Передаточные свойства элементов АСУ в динамическом режиме описывают с помощью динамических характеристик.
Различают следующие формы динамических характеристик:
· обыкновенное дифференциальное уравнение;
· временные характеристики;
· передаточная функция;
· частотные характеристики.
2.4.1. Обыкновенное дифференциальное уравнение
Обыкновенное дифференциальное уравнение является наиболее общей и полной формой описания передаточных свойств элементов АСУ.
Для элемента имеющего один входной сигнал x(t) и один выходной y(t) обыкновенное дифференциальное уравнение в общем случае имеет вид
Ф[ y(t), y¢(t),… y(n)(t); x(t),…x(m)(t), t ] = 0, (2.16)
где t – независимая переменная (обычно время).
Для реальных систем m £ n.
Это уравнение динамики (движения) элемента. Движения в широком смысле слова, когда под движением понимается любое изменение сигналов.
Дифференциальное уравнение (2.16) может быть:
· линейное;
· нелинейное.
Линейное дифференциальное уравнение – уравнение, в котором функция Ф линейна по отношению ко всем ее аргументам, т. е. к y(t), y¢(t),… y(n)(t); x(t),…x(m)(t), t.
Так, например, передаточные свойства четырехполюсника с линейными элементами (рис. 2.9) описываются линейным дифференциальным уравнением вида
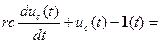0.(2.17)
