Контур бойынша тірелген плитаны есептеу.
Плитаның есебі шектік тепе-теңдік әдісі бойынша орындалады. Басында плитаны бірқалыпты арматураланған деп қабылдайды, яғни плитаның 1м ені бойынша арматураның саны бірдей.
Сурет.Плитадағы июші моментер пайда болу схемасы.
М1- плитаның қысқа бағыты (l1) бойынша аралықтағы шектік июші момент; М2 - плитаның ұзын бағыты ( l2 ) бойынша аралықтағы шектік июші момент;
М1 М1 - плитаның қысқа бағыты (l1) бойынша тіректегі шектік июші момент; Мп, Мп - плитаның ұзын бағыты (l2) бойынша тіректегі июші момент;
Сурет. Плитадағы арматураның жұмыстық стерженьдерді орналастыру схемасы : а) аралықта; б) тіректерде.
АS1- плитаның 1м ені бойынша қысқа бағытына (l1) параллель орналасқан стерженьдердің көлденең қимасының ауданы;
АS2- плитаның 1м ені бойынша ұзын бағытына(l2) параллель орналасқан стерженьдердің көлденең қимасының ауданы;
АSI АSI1- плитаның 1м ені бойынша тіректегі стерженьдердің көлденең
қимасының ауданы; (l2) -ұзындықта;
АsII, А'SII - плитаның 1м ені бойынша тіректегі стерженьдердің көлденең қимасының ауданы ; ( l1 )- ұзындықта;
Июші моменттер кинематикалық тәсілмен анықталады. Шектік тепе-теңдік жағдайда плита қатан бөлшектердің жүйесінен құрастырылады жэне олар бір-бірімен сызықтық пластикалық топсалармен қосылады. Осы жүйесінің сыртқы жэне ішкі күштердің жұмысы анықталады және оларды теңестіріп шектік күшсалмақтар анықтауға болады.
Эксперименттік сынаудың нэтижесінде плитаның қирауы келесі схема бойынша өтетіне белгілі.
Тіректе бөлшектер φ - деген бұрышқа бұрылады, аралықта - 2φ. Плитаның өлшемдері мен салыстырғанда деформациялардың шамалары өте кіші болады, сондықтан
 |

Шектік тепе-теңдік эдістен негізгі теңдеу
 |
Мұндағы: Aq-сыртқы күштердің жұмысы ; AM - ішкі күштердің жұмыс.

V - орналастырудың көлемі; V = Vприз.+Vпирам.;
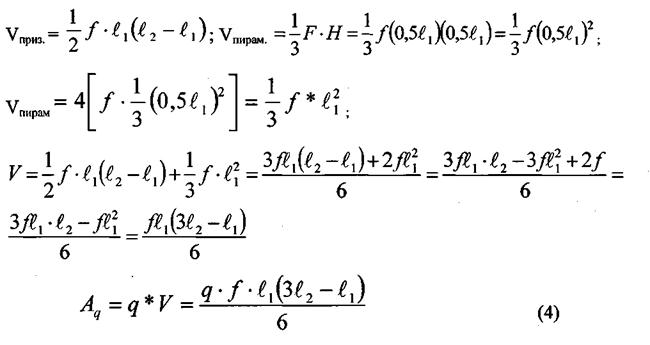 I
I
Плита бірқалыпты арматураланған кезде сызықтық пластикалық топсада июші моменттердің жұмысы ішкі күштердің жұмысы деп айтылады.

Сыртқы жэне ішкі күштердің жұмысы тенестіріледі:
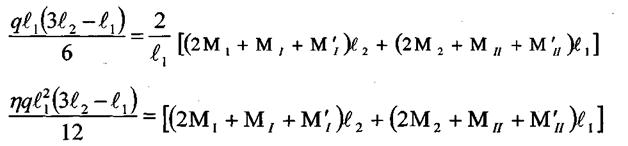
Мұндағы : η - шектік тепетеңдік жағдайда кергіш (распор)күшті пайда болуын ескеретін коэффицент: η=0,8 - ортадағы аралықгаға ; η=0,9 -шектік аралықтарға егер l2/l1<1,5 ; η=1,0 - шеткі аралықтарға егер l2/l1<2;
Шектік июші моменттер келесі формула бойынша анықталады.
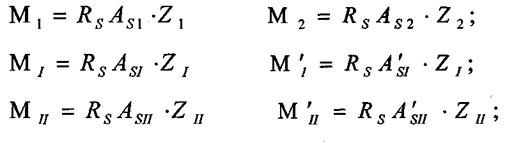
Мұндағы Мұндағы Z1, Z2, ZI, ZII - аралықта жэне тіректе қос күштердің иіні (бетондағы сызылған жэне арматурадағы созылған күштер); Практика жүзінде плитаның есебінің 2 түрі кездеседі:
1 -түрі: Арматураның көлденең стерженьдердің ауданы белгілі.
Шектік күшсалмақтардың мөлшерін анықтау керек (q). Моменттердің шамасын (7) формула бойынша табу керек және осы моменттердің (6) тепе-теңдік теңдеуге қойып шектік ьсүшсалмақтардың мөлшерін табамыз.
2 - түрі: Арматураның көлденең стерженьдердің ауданың анықтау (AS1, AS2, ASI/, ASII, ASIII/) керек.
Плитаның калыңдығы келесі шарттар бойынша қабылданады:

(6) - теңцеуде барлық алты моменттер белгісіз.осы моменттерді (7)- формула бойынша анықтау үшін барлық арматураның көлденең қимасының аудандарың AS1 арқылы табу керек.
Практикада келесі нүсқауларды қолданады:
А) 1 кестеде плитаның ұзындықтардың қатынасына ( l2 / l1 ) байланысты плитаның аралықтағыарматураның көлденең қимасының аудандардың (AS1, AS2) қатынасы беріледі. Кестенің мэліметтері бойынша l2 / l1 = (1-2) өзгерген кезде AS1, AS2 = (0,15-2,0) аралығы болады.
1 кесте

Б) 2- кестеде плитаның ұзындықтардың қатынасы (l2 / l1) байланысты плитаның теректердегі арматураның көлденең қимасының аудандардың (AS1/AS1;ASI/AS1; ASII/AS1; ASII/ AS1) қатынастары (1-2,5) аралығында болады.
2 кесте
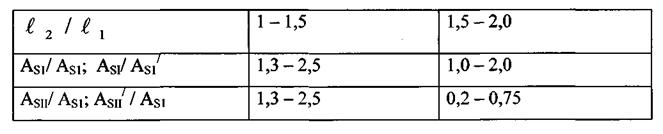
Жоғарғы ұсыныстарды қолданған кезде (6) формулада тек қана (ASI) белгісіз болады. Осы формула бойынша АSI анықталады жэне берілген қатынастар арқылы АS2, АSI, А'SI,А8ІІ, А'8ІІ табылады.
Бақылау сұрақтары:
1. Контур бойынша тірелген плиталы тұтас қырлы қабатаралық жабындардың конструктивтік жүйесін үйлестіру
2. Контур бойынша тірелген плиталы тұтас қырлы қабатаралық жабындардың 1 түрі
3. Контур бойынша тірелген плиталы тұтас қырлы қабатаралық жабындардың 2 түрі
4. Контур бойынша тірелген плиталы арматуралау схемасы
5. Контур бойынша тірелген плитадағы июші моменттердің пайда болу схемасы
6. Контур бойынша тірелген плитаның қирау схемасы
7. Плита есептеудің шектік тепе-теңдік әдістің негізгі теңдеуі
8. Плитадағы шектік июші моменттердің формуласы
9. Контур бойынша тірелген плитадағы аралықтарда және тіректерде арматураның көлденең қимасының ауданын анықтау
Ұсынылатын әдебиеттер тізімі
1. Байков В.Н., Сигалов Э.Е. Железобетонные конструкции. Общий курс.-М.:Стройиздат,1991.-767 с.
2. Сахи Д.М. Темірбетон конструкциялары.-Тараз, 1998.-99 б.
3. Сахи Д.М., Сахи Қ. Темірбетон конструкцияларын есептеу және жобалау.- Тараз, 2003.-176 б.
4. Әбілдинов А. Темірбетонды конструкциялауды есептеу негіздері. Оқу құралы.-Алматы:РБК, 1995.-149 б.
5. Мандриков А.П. Темірбетон конструкцияларын есептеудің мысалдары. Оқу құралы. І-бөлім.-Алматы:РБК,1996.-229 б.
Оразбаев Ж.И., Сахиев К.С., Сахиев Д.М. Құрастырмалы темірбетон арқалықты жобалау.-Шымкент: КазХТИ, 1994.-43 б.