Частные коэффициенты эластичности.
Таблица 1
Формулы расчета коэффициентов эластичности для различных типов уравнений регрессии.
В зависимости от вида зависимости между х и у формулы расчета коэффициентов эластичности будут меняться. Основные формулы для наиболее часто используемых типов уравнений регрессии приведены в таблице:
Вид функции,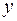 
| Первая производная, 
| Средний коэффициент эластичности, 
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
|
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
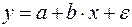
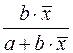
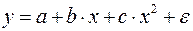
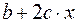
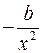
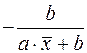
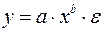
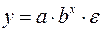
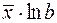
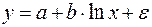
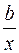
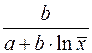
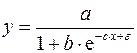
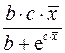
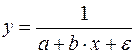
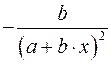
Только для степенных функций 
коэффициент эластичности представляет собой постоянную независящую от х величину, равную в данном случае параметру b.
Возможны случаи, когда расчет коэффициента эластичности не имеет смысла. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения в процентах. Например, на сколько процентов изменится заработная плата с ростом стажа работы на 1%? В такой ситуации степенная функция, даже если она оказывается наилучшей, не может быть экономически интерпретирована. Например, изучая соотношение ставок межбанковского кредита у (в процентах годовых) и срока его предоставления х (в днях), было получено уравнение регрессии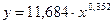 
с очень высоким показателем корреляции (0,98). Коэффициент эластичности 0,352% лишен смысла, ибо срок предоставления кредита не измеряется в процентах. Значительно больший интерес для этой зависимости может представить линейная функция 
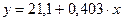, имеющая более низкий показатель корреляции 0,85. Коэффициент регрессии 0,403 показывает (в процентах) изменение ставок кредита с увеличением срока его предоставления на один день.
В линейной модели множественной регрессии если факторные признаки различны по своей сущности или имеют различные единицы измерения, коэффициенты регрессии bj являются несопоставимыми. Поэтому уравнение регрессии дополняют соизмеримыми показателями тесноты связи фактора с результатом, позволяющими ранжировать факторы по силе влияния на результат. К таким показателям относятся частные коэффициенты эластичности.
Частные коэффициенты эластичности рассчитываются по формуле:
,
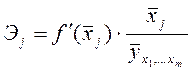где 
- среднее значение фактора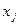 
;
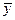- среднее значение результата у.
Частный коэффициент эластичности показывает, насколько процентов в среднем изменяется результат у с увеличением фактора 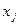на 1% от своего среднего уровня при фиксированном положении других факторов модели. В случае линейной зависимости коэффициенты эластичности рассчитываются по формуле:
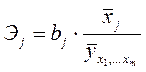
где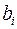 
– коэффициент регрессии для фактора 
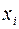в уравнении множественной регрессии.
Наряду с частными коэффициентами эластичности могут быть найдены средние по совокупности показатели эластичности:
,
которые показывают, на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.