Активность и коэффициент активности электролитов. Средняя ионная активность и средний ионный коэффициент активности
В связи с электростатическим взаимодействием в растворе даже для разбавленных растворов сильных электролитов концентрации в уравнениях термодинамики должны быть заменены активностями. Например, если для иона как и для компонента в растворе справедливо выражение:
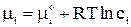 , (5)
, (5)
где сi – концентрация i-го иона в идеальном растворе, то для реального раствора будем иметь:
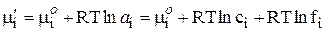 , (6)
, (6)
где ai = ci·fi — активность i-го иона в растворе,
fi – коэффициент активности.
Тогда энергия взаимодействия иона с окружающими его ионами в расчете на 1 моль ионов равна
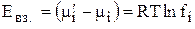 , (7)
, (7)
fi→1 при с→0
Таким образом, величина коэффициента активности, главным образом зависящая от силы электростатического взаимодействия ионов, а также ряда других эффектов, характеризует степень отклонения свойств реальных растворов электролитов от идеальных растворов. По смыслу fi это работа по переносу иона из идеального раствора в реальный.
Различают активность электролита и активность ионов. Для любого электролита процесс диссоциации можно записать следующим образом:
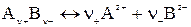 , (8)
, (8)
где n+ и n– — количество ионов А с зарядом z+ и ионов B c зарядом z–, на которые распадается исходная частица.
Для раствора электролита в целом можно записать:
mсоли = m0соли + RT·ln aсоли, (9)
С другой стороны химический потенциал электролита складывается из химических потенциалов ионов, так как электролит распадается на ионы:
mсоли = n+ m+ + n- m-, (10)
m+ и m- относятся к одному молю ионов, mсоли – к одному моль электролита. Подставим выражение (10) в (9):
n+ m+ + n- m- = m0соли + RT ln aсоли (11)
Для каждого типа ионов можем записать уравнение типа (9):
m + = m0+ + RT·ln a+
m - = m0- + RT·ln a- (12)
Подставим уравнение (12) в левую часть уравнения (11) и поменяем местами правую и левую части.
m0с + RT·ln aс = n+ m0+ + n+RT·ln a+ + n– m0– + n- RT·ln a- (13)
Объединим все слагаемые с m0 в левой части
(m0с - n+ m0+ - n- m0- ) = n+ RT·ln a+ + n- RT·ln a- - RT·ln aсоли (14)
Если учесть, что по аналогии с формулой (10)
m0С = n+ m0+ + n- m0- (15)
то m0С - n+ m0+ - n- m0- = 0 (16)
Уравнение (15) аналогично уравнению (10), но оно относится к стандартному состоянию, когда (аС = а+ = а- = 1). В уравнении (14) правая часть равна нулю, и оно перепишется следующим образом:
RT·ln aс = n+ RT·ln a+ + n- RT·ln a-
ln aс = ln a+n+ + ln a+n-
 , (17)
, (17)
Это связь активности электролита в растворе с активностями ионов
где аС — активность электролита, а+ и а– — активности положительных и отрицательных ионов. Например, для бинарных электролитов АВ справедливо:

 , следовательно
, следовательно 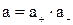
Нельзя принципиально найти экспериментально активности отдельных ионов, т.к. нужно было бы иметь дело с раствором из одного вида ионов. Это невозможно. Поэтому было введено понятие средней ионной активности ( ), представляющей собой среднее геометрическое из активности отдельных ионов:
), представляющей собой среднее геометрическое из активности отдельных ионов:
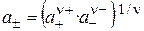 , где
, где  . (18)
. (18)
или подставив выражение (17) имеем:
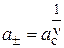 ,
,  (19)
(19)
Криоскопический метод и метод, основанный на определении давления пара, позволяют определить активность электролита в целом (аС) и по уравнению (19) найти среднюю ионную активность.
Во всех случаях, когда возникает необходимость подстановки величины а+ или а– в какое-то уравнение, эти величины заменяют средней активностью данного электролита а±, например,
а± » а+ » а–
Как известно, активность связана с концентрацией соотношением a=f∙m. Средний ионный коэффициент активности (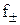 ) определяется выражением, аналогичным выражению для средней ионной активности
) определяется выражением, аналогичным выражению для средней ионной активности
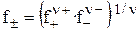 . (20)
. (20)
Существуют табличные значения  для различных способов выражения концентраций (моляльность, молярность, мольные доли). Для них
для различных способов выражения концентраций (моляльность, молярность, мольные доли). Для них  имеет численно разные значения. Экспериментально значения
имеет численно разные значения. Экспериментально значения  определяют криоскопическим методом, методом измерения давления пара, методом измерения ЭДС гальванических элементов и др.
определяют криоскопическим методом, методом измерения давления пара, методом измерения ЭДС гальванических элементов и др.
Аналогично средний ионный стехиометрический коэффициент n± определяется из выражения:
 (21)
(21)
Средняя ионная моляльность ( ) определяется как
) определяется как
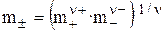 . (22)
. (22)
Если концентрацию раствора выражать через моляльность, то
 .
.
и, подставив выражения
m+=ν+m, m-=ν-m,
где m ‑ моляльность раствора, будем иметь:
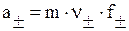 . (23)
. (23)
Пример 7.1. Найти связь между активностью электролита, его моляльной концентрацией и средним ионным коэффициентом активности для растворов NaCl и Na2CO3 моляльности m.
а) Концентрации ионов, образующихся при полной диссоциации NaCl, равны m:
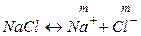 .
.
Так как n+ = n– = 1, то
 .
.
Для равновалентных электролитов средняя моляльность будет равна общей моляльности электролита:
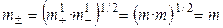 .
.
Тогда
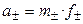 ,
,
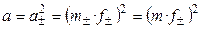 .
.
б) Концентрации ионов, образующихся при полной диссоциации Na2CO3, равны
 .
.
Так как n+ = 2, n– = 1, то  .
.
 ,
,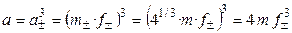 .
.