Алгебраический метод решения задач на построение.
При решении задач на построение алгебраическим методом:
1) составляют уравнение или систему уравнений по условию задачи;
2) решают полученное уравнение или систему и находят нужное неизвестное;
3) осуществляют геометрическое построение по полученной формуле.
Прежде чем переходить к примерам, разберем основные задачи,  применяемые при алгебраическом методе (нумерация является продолжением нумерации основных задач ). Укажем только решение этих задач, а обоснование предоставляется читателю.
применяемые при алгебраическом методе (нумерация является продолжением нумерации основных задач ). Укажем только решение этих задач, а обоснование предоставляется читателю.
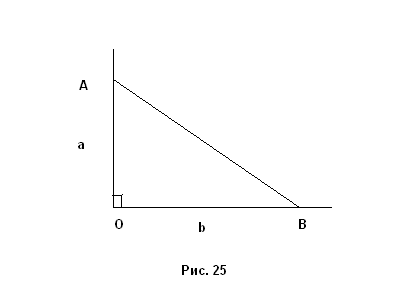
Задача 13. Даны отрезки а и b. Построить отрезок 
Решение. Строим прямой угол с вершиной О (рис.25 ). На его сторонах откладываем отрезки ОА=a и ОВ=b. Тогда отрезок АВ является искомым.
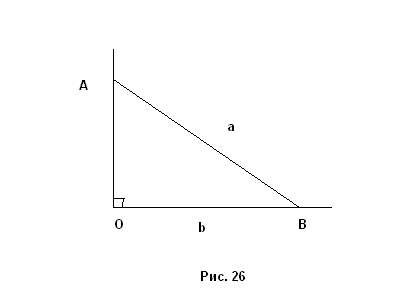
Задача 14. Даны отрезки а и b. Построить отрезок 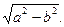
Решение. Строим прямой угол с вершиной в точке О (рис.26). На одной из его сторон откладываем отрезок ОВ=b. Проводим окружность с центром в точке В и радиуса a. Она пересечет вторую сторону угла в точке А. Отрезок ОА является искомым.
Задача 15. Даны отрезки а и b. Построить отрезок 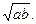
Решение. На отрезке АВ=a+b, как на диаметре строим окружность. Пусть C такая точка на АВ, что АС=a. В точке С восстанавливаем перпендикуляр к АВ. Он пересечет окружность в точке Д. Отрезок СД искомый (рис.27). Он называется средним геометрическим отрезков a и b.
 Задача 16. Даны отрезки а , b и с. Построить отрезок
Задача 16. Даны отрезки а , b и с. Построить отрезок 
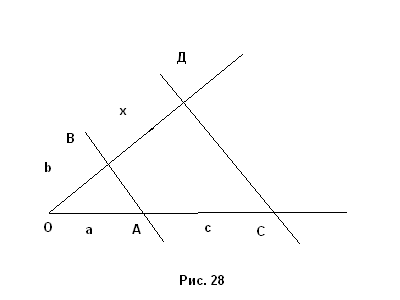
Решение. Строим произвольный угол с вершиной в точке О (рис.28). На одной из его сторон откладываем последовательно отрезки ОА=a и АС=c, а на второй ОВ=b. Через точку С проводим прямую, параллельную АВ. Она пересечет вторую сторону угла в точке Д. Отрезок ВД искомый. Его называют четвертым пропорциональным отрезком.
ПРИМЕР 20. Даны отрезки a,b и с. Построить отрезок 
Построение.
1) строим отрезок 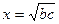 ;
;
2) строим отрезок 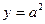 , как четвертый пропорциональный отрезков a,a,1;
, как четвертый пропорциональный отрезков a,a,1;
3) строим отрезок 
ПРИМЕР 14. Даны отрезки a и b. Построить отрезок 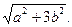
Построение.
1) строим отрезок 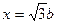 , как катет прямоугольного треугольника с гипотенузой 2b и вторым катетом b;
, как катет прямоугольного треугольника с гипотенузой 2b и вторым катетом b;
2) строим отрезок 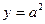 , как четвертый пропорциональный отрезков a,a,1;
, как четвертый пропорциональный отрезков a,a,1;
3) строим отрезок 
ПРИМЕР 24. Даны окружность и точка А вне ее. Из этой точки провести секущую так, чтобы она делилась окружностью пополам.
Анализ. Зная положение точки относительно круга, можно построить касательную, длина которой известна и пусть она равна a. Пусть АС – секущая и В – ее середина, АВ=ВС=x. По формуле зависимости секущей и касательной, проведенной из одной точки, имеем  . Отсюда
. Отсюда 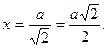 Полученный отрезок представляет собой половину гипотенузы равнобедренного прямоугольного треугольника с катетом a (рис.29).
Полученный отрезок представляет собой половину гипотенузы равнобедренного прямоугольного треугольника с катетом a (рис.29).
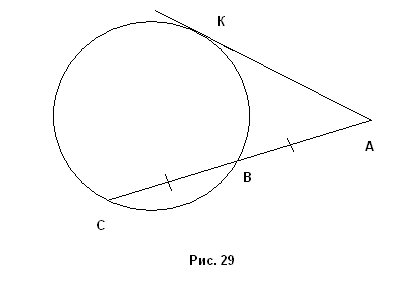
Построение. Найдем длину касательной, проведенной из точки А к данной окружности. Затем построим равнобедренный прямоугольный треугольник с катетом a и его гипотенузу разделим пополам. Получим отрезок x. Построим окружность с центром в точке А и радиусом, равным x. Она пересечет данную окружность в точке В. Построим луч АВ, он и даст нам искомую секущую.
Доказательство следует из построения.
Анализ. Количество решений задачи зависит от длины отрезка АО, где О – центр данной окружности. Пусть АО пересечет данную окружность в точке С и R – радиус данной окружности.
1) Если x+R<AO, то задача имеет два решения;
2) Если x+R=AO, то задача имеет одно решение;
3) Если x+R>AO, то задача не имеет решения.
Одна из основных целей при обучении математике – научить школьников правильно и хорошо решать задачи.
Учитель математики должен в совершенстве владеть рассмотренными нами основными общими методами решения математических задач и постепенно вооружать ими своих учеников. Без этого невозможен успех в обучении математике.
Известный американский математик Дж. Пойа, посвятил проблеме поиска решения задачи специальное исследование (Дж. Пойа Как решать задачу. Учпедгиз, 1961). Особое внимание в этом труде он уделяет анализу и синтезу при поиске решения.
В конце книги он приводит таблицу, которой следует придерживаться при отыскании решения задачи. Приведем ее краткий вариант.
1. Понять предложенную задачу.
Что гласит задача? Что дано? Что нужно найти? Определено ли неизвестное данными задачи? Или они недостаточны, или же чрезмерны?
2. Найти путь от неизвестного к данным, если нужно, рассмотреть промежуточные задачи («анализ»). Составить план решения.
Сформулировать отношения между неизвестным и данными. Преобразовать (или ввести новое) неизвестное, сближая его с данными. Преобразовать данные, получив новые элементы, более близкие к искомому. Вспомнить решение аналогичной задачи. Все ли данные использованы? Нельзя ли сформулировать задачу иначе? Обобщить. Рассмотреть частные случаи.
3. Реализовать найденную идею решения («синтез»).
Обосновать правильность каждого шага.
4. Решение проверить и оценить критически.
Правдоподобен ли результат? Почему? При возможности сделать проверку. Нельзя ли решить иначе, более прямым путем?
При изучении и восприятии задачи, каждый ученик должен знать и постоянно соблюдать разумное и обязательное правило: не приступать к решению задачи или поиску пути ее решения до тех пор, пока не убедился, что текст задачи полностью изучен и ясно понят, что осмыслены все данные и требования задачи, осознан характер функциональных зависимостей между входящими в задачу величинами, искомой и известными. Подобные методические правила постигаются учащимися в процессе практического их применения. Задачу со сложным текстом рекомендуется внимательно читать несколько раз. При фронтальной работе с классом учитель с помощью вопросов проверяет детальность и точность, полноту и сознательность восприятия задачи каждым учеником.
Главным этапом процесса решения задачи является поиск пути решения. Здесь наиболее эффективны различные аналитические методы и приемы, которыми школьники должны постепенно овладевать. Для этой цели потребуется постоянное внимание и усилия со стороны учителя, поскольку учащиеся обычно склонны сразу применять синтетический метод, мало пригодный для отыскания неизвестного пути решения задачи. Если же трудности встретятся и при аналитическом поиске, то ученик может попытаться вести свой поиск и по встречному, синтетическому направлению с целью сближения тех и других результатов.
Облегчению поиска пути служит наглядное, предметно реальное представление условия задачи, описанных в ней процессов, различное использование графических средств, схем с умело расставленными данными, применение вспомогательных и частных эвристических приемов.
Одной из важнейших целей, стоящих перед решением задач в курсе математики, является обучение школьников решать задачи самостоятельно. Для достижения этой цели необходимо учить поискам пути решения задачи. Опытный учитель не спешит сообщить ученикам решение задачи, а попытается вместе с учениками отыскать путь ее решения. При этом школьники приобретут определенный опыт как в решении, так и в его поиске.
Чертеж геометрической фигуры к решаемой задаче должен быть правильным, полностью соответствовать как условию задачи, так и следствиям из него. Можно рекомендовать следующее правило: чертеж делать после того, как имеется уже четкое представление о заданной фигуре, о связях между ее элементами, вытекающими из условия задачи. Конечно, сразу нарисовать правильный и точный чертеж не всегда удается, поэтому нужно учить учеников делать хорошие чертежи, постепенно используя условия задачи, отражая их на чертеже и переделывать чертеж, если данные задачи не точно на нем отражены. Также следует приучать школьников переделывать чертеж, если в процессе решения открылись новые данные, которые отсутствуют на чертеже
Учащиеся должны знать, что во избежание ошибок чертеж должен быть правильным, однако все, что используется в решении, кроме того, что известно по условию задачи, должно быть доказано логически с использованием теории предмета.
Еще одним из требований к учителю, является то, что нужно обучать учащихся поиску нескольких различных способов решения задачи (если они существуют). Это позволит развить в большем объеме логику мышления, позволят школьнику увидеть связь различных разделов математики, ее единство, научит поиску рациональных способов решения.
Учителю также необходимо постоянно совершенствоваться в плане решения задач. Не стоит останавливаться на задачах из учебника. Необходимо постоянно читать методическую литературу, статьи в методических журналах, посвященные методам решения задач. Учителю также нужно стремиться к созданию своего «банка задач», где будут собраны интересные с его точки зрения задачи, которые позволят разнообразить процесс обучения, развить интерес к предмету, а также помогут занять тех учащихся на уроке, которые уже научились решать типовые задачи.