Геометрические места точек.

Определение.Геометрическим местом точек (в дальнейшем ГМТ), называется фигура плоскости, состоящая из точек обладающих некоторым свойством, и не содержащая ни одной точки, не обладающей этим свойством.

Мы будем рассматривать только те ГМТ, которые можно построить с помощью циркуля и линейки.

Рассмотрим ГМТ на плоскости, обладающие простейшими и наиболее часто выражающимися свойствами.

1). ГМТ, отстоящих на данном расстоянии r от данной точки О, есть окружность с центром в точке О радиуса r.

2). ГМТ равноудаленных от двух данных точек А и В, есть прямая, перпендикулярная к отрезку АВ и проходящая через его

середину.

3). ГМТ равноудаленных от двух данных пересекающихся прямых, есть пара взаимно перпендикулярных прямых, проходящих через точку пересечения и делящих углы между данными прямыми пополам.

4). ГМТ, отстоящих на одинаковом расстоянии h от прямой, есть две прямые, параллельные этой прямой и находящиеся по разные стороны от нее на данном расстоянии h.

5). Геометрическое место центров окружностей, касающихся данной прямой m в данной на ней точке М, есть перпендикуляр к АВ в точке М (кроме точки М).

6). Геометрическое место центров окружностей, касающихся данной окружности в данной на ней очке М, есть прямая, проходящая через точку М и центр данной окружности (кроме точек М и О).

7). ГМТ, из которых данный отрезок виден под данным углом, составляет две дуги окружностей, описанных на данном отрезке и вмещающих данный угол.

8). ГМТ, расстояния от которых до двух данных точек А и В находятся в отношении m : n, есть окружность (называемая окружностью Аполлония).

9). Геометрическое место середин хорд, проведенных из одной точки окружности, есть окружность, построенная на отрезке, соединяющем данную точку с центром данной окружности, как на диаметре.

10). Геометрическое место вершин треугольников равновеликих данному и имеющих общее основание, составляет две прямые, параллельные основанию и проходящие через вершину данного треугольника и ему симметричного относительно прямой, содержащей основание.

Приведем примеры отыскания ГМТ.

 

ПРИМЕР 2. Найти ГМТ, являющихся серединами хорд,

проведенных из одной точки данной окружности

(ГМТ № 9).

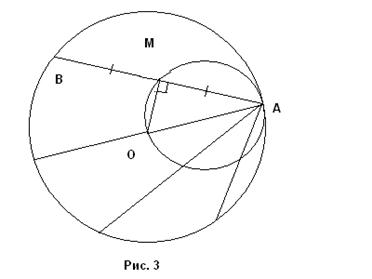
Решение. Пусть дана окружность с центром О и на этой окружности выбрана точка А из которой проводятся хорды. Покажем, что искомое ГМТ есть окружность, построенная на АО как на диаметре (кроме точки А) (рис.3).

Пусть АВ - некоторая хорда и М – ее середина. Соединим М и О. Тогда МО ^ АВ (радиус, делящий хорду пополам, перпендикулярен этой хорде). Но, тогда ÐАМО = 90⁰. Значит М принадлежит окружности с диаметром АО (ГМТ № 7). Т.к. эта окружность проходит через точку О, то О принадлежит нашему ГМТ.

Обратно, пусть М принадлежит нашему ГМТ. Тогда, проведя через М хорду АВ и соединив М и О, получим, что ÐАМО = 90⁰, т.е. МО ^ АВ, а, значит, М – середина хорды АВ. Если же М совпадает с О, то О - середина АС.

 

Часто метод координат позволяет находить ГМТ.

 

ПРИМЕР 3. Найти ГМТ, расстояние от которых до двух данных точек А и В находятся в данном отношении m : n (m ≠ n).

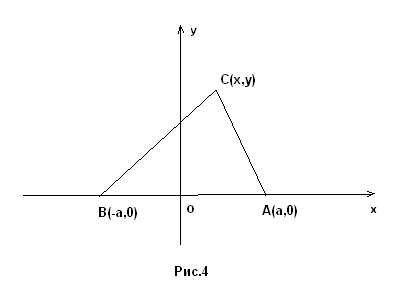
Решение. Выберем прямоугольную систему координат так, чтобы точки А и В располагались на оси Ох симметрично относительно начала координат, а ось Оу проходила через середину АВ (рис.4). Положим АВ = 2a. Тогда точка А имеет координаты А (a, 0), точка В - координаты В (-a, 0). Пусть С принадлежит нашему ГМТ, координаты С(х, у) и CB/CA=m/n. Но 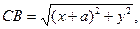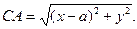Значит

(*)

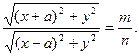Преобразуем наше равенство. Имеем

 

 

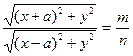
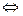
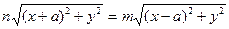
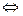
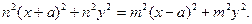
После раскрытия скобок и приведения подобных слагаемых, получаем

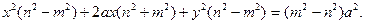Разделим левую и правую части последнего неравенства на 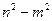(это можно сделать, так как по условию 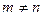), затем выделим полный квадрат относительно х. Получаем

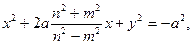
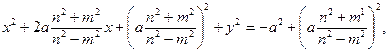или

 

(**)

 

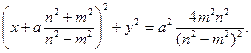Но последнее уравнение задает окружность с центром в точке 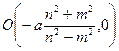и радиусом 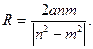Таким образом, если точка удовлетворяет условиям задачи, то она принадлежит (**).

Обратно, пусть координаты точки С(x,y) удовлетворяют уравнению (**). Проделывая все выкладки в обратную сторону, приходим к равенству (*), что и доказывает принадлежность точки С нашему ГМТ.