Алгебраический анализ
Под алгебраическим анализом мы будем понимать метод решения задач с помощью уравнений, систем уравнений или неравенств.
Этот метод имеет явно выраженные общие черты аналитического метода. Так, решая задачу с помощью уравнений, отправляются от неизвестного ( или неизвестных, если составляют систему уравнений). В качестве неизвестного (неизвестных), как правило, выступает искомое (искомые) основной задачи. Но иногда, для получения более простого решения целесообразно отправляться при составлении уравнения от вспомогательного неизвестного. В последнем случае имеет место преобразование основной задачи в серию из двух вспомогательных задач, первая из которых решается методом алгебраического анализа, а вторая – арифметически.
Второй основной этап применения алгебраического анализа – решение полученного уравнения (системы уравнений) и получение корней. На этом этапе важно следить за равносильностью преобразований, чтобы в итоге получить множество всех решений основной задачи и только его.
На третьем этапе предстоит выяснить достоверность полученных решений, отбросив те, которые не подходят по смыслу задачи. Например, если речь идет о длине отрезка, а в процессе решения появились отрицательные корни, то они, очевидно, не подходят. Иногда достоверность решения проверяется с помощью каких-то известных фактов (равенств, неравенств и т.д.). Если речь в задаче шла о длинах сторон треугольника, то ответ следует проверить на выполнение неравенства треугольника.
Приведем пример задачи, для решения которой введение новых промежуточных неизвестных позволяет упростить решение.
Задача. Из пункта А в пункт В вышел пассажирский поезд, и в тоже время из В в А вышел товарный поезд. Пассажирский поезд прибыл к месту назначения через 9 часов, а товарный – через 16 часов после встречи. Определить, какое время находился в пути каждый поезд.
Р е ш е н и е. Обозначим через х и у скорости соответственно пассажирского и товарного поездов, а через t – их время движения до встречи. Тогда по условию задачи можно составить систему
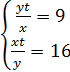 .
.
Перемножая эти уравнения, получим 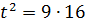 , или
, или 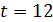 . Значит до встречи поезда двигались 12 часов. Но тогда пассажирский поезд на весь путь затратил 12+9=21 час, а товарный – 12+16=28 часов.
. Значит до встречи поезда двигались 12 часов. Но тогда пассажирский поезд на весь путь затратил 12+9=21 час, а товарный – 12+16=28 часов.
Ответ. Пассажирский поезд на весь путь затратил 21 час, а товарный – 28 часов.
Задачи на построение традиционно занимают важное место в школьном курсе математики, поскольку они являются существенным фактором математического образования и представляют собой мощное средство геометрических исследований.
История возникновения задач на построения уходит своими корнями в далекую древность, и необходимость решения таких задач вытекает из практики. До нас дошли знаменитые сооружения старины (пирамиды, тоннели, храмы, здания и т.п.) строительство которых требовало развития навыков и теории измерений на местности. Кроме этого имеются сведения о попытке еще во времена Аристотеля измерить длину земного меридиана (IV – III в.до н.э.). Все это привело к созданию теории решения задач на построение.
Решение задач на построение осуществляется, как правило, с помощью циркуля и линейки, причем с помощью циркуля мы можем проводить окружности любого ненулевого радиуса, а с помощью линейки можем строить прямые.
Давно было замечено, что циркуль является более точным, более совершенным инструментом, чем линейка, что некоторые построения можно выполнить только с помощью одного циркуля, например, разделить окружность на шесть равных частей, построить точку, симметричную данной и т.д. Все это послужило толчком к исследованию геометрических построений, выполняемых одним лишь циркулем. И в 1672 году Г.Мор доказал, что все геометрические построения, выполнимые с помощью циркуля и линейки, можно выполнить с помощью одного только циркуля. А в 1833 г Я. Штейнер доказал, что всякая задача на построение, разрешимая циркулем и линейкой, может быть решена и одной линейкой, если в плоскости чертежа дана постоянная окружность и ее центр.
Решить задачу на построение с помощью циркуля и линейки - значит, свести ее к выполнению определенного числа операций: провести прямую через две точки; найти точку пересечения прямых; провести окружность с известным центром и данным радиусом; определить точки пересечения прямой и окружности, двух окружностей. Будем называть такие операции элементарными.
Решение задачи на построение состоит из четырех этапов.
1. Анализ. Предполагается, что задача решена и требуемая фигура построена. Используя различные теоремы геометрии, свойства фигур, выясняем соотношения между элементами требуемой фигуры, которые помогут решить задачу. (Таким образом, первая часть решения задачи на построение проводится аналитическим методом).
Когда при помощи анализа зависимость между данными и искомыми величинами определена, переходят ко второй части решения – построению.
2. Построение. Этот этап представляет собой выполнение тех операций, которые были выведены из плана решения задачи, т.е. из анализа. Т.е. построение проходит с помощью синтетического метода решения задач.
3. Доказательство.Когда построение выполнено и искомая фигура построена, необходимо доказать, что она действительно удовлетворяет всем требованиям задачи.
4. Исследование.На этом этапе следует выяснить, при каких условиях на данные в условии задачи решение существует и количество возможных решений.
ПРИМЕР 1. Пересечь треугольник прямой, параллельной основанию
так, чтобы отрезок, заключенный между боковыми
сторонами, был равен сумме отрезков боковых сторон,
считая от основания (рис 1).
 Анализ. Допустим, что задача решена. Через точку М проходит прямая, отрезок КН которой удовлетворяет данным в условиях задачи, т.е КН ║ АВ и КН = АК + НВ или АК = КМ, НВ = МН. Соединим точку М с точками А и В. Полученные треугольники АКМ и ВНМ будут равнобедренными, т.к. АК = КМ, ВН = МН.
Анализ. Допустим, что задача решена. Через точку М проходит прямая, отрезок КН которой удовлетворяет данным в условиях задачи, т.е КН ║ АВ и КН = АК + НВ или АК = КМ, НВ = МН. Соединим точку М с точками А и В. Полученные треугольники АКМ и ВНМ будут равнобедренными, т.к. АК = КМ, ВН = МН.
Значит, ÐКАМ = ÐКМА и ÐМВН = ÐНМВ. Но, ÐКМА = ÐМАС и ÐНМВ = ÐМВА (как накрест лежащие углы при параллельных прямых и секущей).
Тогда ÐКАМ = ÐМАС и ÐНВМ = ÐМВА, т.е. АМ и ВМ - биссектрисы углов А и С.
Построение. Проведем биссектрисы углов А и В и через их точку пересечения М проведем КН ║ АВ.
Доказательство. Треугольники АКМ и ВНМ равнобедренные, т.к. ÐКАМ = ÐМАВ = ÐКМА, ÐМВН = ÐМВА = ÐВМН. Значит, АК = КМ, ВН = НМ и КН = КМ + МН = АК + НВ.
Исследование. Задача всегда определена и имеет единственное решение, т.к. биссектрисы углов треугольника пересекаются в одной точке.
При изучении планиметрии в школе рассматриваются следующие основные задачи на построение:
1. Построить треугольник по трем сторонам;
2. Построить угол равный данному;
3. Построить треугольник по двум сторонам и углу между ними;
4. Построить треугольник по стороне и двум прилежащим к ней углам;
5. Построить прямую, перпендикулярную данной прямой и проходящей через данную точку;
6. Построить прямую, перпендикулярную к данному отрезку и проходящую через его середину;
7. Построить биссектрису данного угла;
8. Построить касательную к данной окружности в данной ее точке;
9. Построить прямоугольный треугольник по гипотенузе и острому углу;
10. Построить прямоугольный треугольник по гипотенузе и катету;
11. Построить касательную к данной окружности, проходящую через данную точку;
12. Построить треугольник по двум сторонам и углу, лежащему против одной из них.
Ниже мы еще рассмотрим ряд основных задач.
Эти задачи считаются известными и их решение приводить не стоит (хотя следует иметь в виду, что решение этих задач должно быть известно учащимся и они должны быть готовы рассказать их решение по требованию учителя).
Поэтому, решить задачу на построение с помощью циркуля и линейки - значит, составить алгоритм с помощью которого можно осуществить построение данной фигуры; в качестве команд алгоритма выступают либо элементарные , либо основные задачи.