Синтетический метод решения

Необходимое условие решения сложной задачи – умение решать простые задачи, к которым сводится любая сложная задача. При наличии такого умения вся проблема состоит в том, чтобы найти ту совокупность простых задач, решение которых приведет к выполнению требования основной задачи. Здесь возможны два основных пути поиска решения: синтетический и аналитический.

Как ученики обычно решают сложную задачу? Они берут любое данное в условии задачи и к нему присоединяют какое-либо из остальных данных. Если эти данные образуют простую задачу, то ее решают; если простой задачи не получилось, образуют другую пару данных и в результате решения первой простой задачи получают первое вспомогательное данное. Используя вспомогательное данное и какое-либо из остальных данных основной задачи, решают вторую простую задачу и получают второе вспомогательное данное и т.д. до тех пор, пока не получат такой простой задачи, результат которой является искомым основной задачи.

Это и есть синтетический метод решения задач.

Если основную задачу условно записать: А У, а первую и последнюю из конечной совокупности простых задач, из которых состоит решение основной задачи, обозначить соответственно через а₁ и а_n, то процесс решения задачи синтетическим методом можно записать в виде:

.

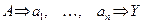Рассмотрим этот метод на примере.

Задача. Две машины убирают снег за 6 часов. Однажды, после 3 ч совместной работы, первую машину отправили в другой район города, а оставшаяся машина закончила уборку за 5 ч. За сколько часов каждая машина отдельно может выполнить всю работу?

Р е ш е н и е.

1) Какую часть всей работы выполнили две машины, работая вместе?

3 : 6 = 0,5

2) Какую часть всей работы выполнила вторая машина, после ухода первой?

1 – 0,5 = 0,5

3) За сколько часов могла бы выполнить всю работу вторая машина, работая отдельно?

5 : 0,5 = 10

4) Какую часть всей работы выполнила вторая машина за 3ч?

3 : 10 = 0,3

5) Какую часть работы выполнила первая машина за 3 ч?

0,5 – 0,3 = 0,2

6) За сколько часов могла бы выполнить всю работу первая машина отдельно?

3 : 0,2 = 15

О т в е т : 15ч и 10ч.

Если решение задачи записывается кратко, то необходимо требовать от учеников уметь осознано и правильно формулировать вопросы к каждому действию или пояснять результат полученных вычислений, чтобы исключить случайное совпадение отвлеченных чисел.

Синтетический метод широко применяется не только при решении задач арифметическим способом, но и при решении геометрических задач на вычисление и построение (см. след. пункт).

Рассмотрим краткое решение задачи по геометрии на вычисление.

Задача. В трапеции АВСD диагональ АС перпендикулярна CD и длина проекции CD на основание AD равна 5. Найти длины сторон трапеции, если боковая сторона АВ перпендикулярна основаниям и ВС = 2АВ.

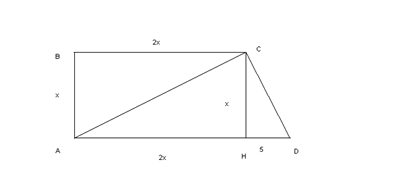Р е ш е н и е.

1) Пусть АВ = х. Тогда ВС =АН = 2х, СН = х.

2) В прямоугольном треугольнике АСD СН² = АН ∙ НD, или 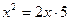. Значит х = 10.

3) АВ= 10, ВС= 20, AD = 25.

4) Из прямоугольного треугольника СHD по теореме Пифагора: .

О т в е т : АВ= 10, ВС = 20, СD = , DA = 25.

Основной недостаток синтетического метода – отсутствие какого бы ни было критерия в вопросе, с чего, с каких данных начинать решение и какие вспомогательные величины определять, какие простые задачи решать в дальнейшем, чтобы решить основную задачу. Этот метод мало пригоден для отыскания новых решений и слабо способствует научению школьников самостоятельно решать задачи, логически рассуждать, продуктивно мыслить. Пользуясь синтетическим методом, учащиеся нередко выполняют лишнюю работу, а иногда слабый ученик может предложить бессмысленное действие.

Единственное, на что можно в некоторой степени можно опереться, применяя синтетический метод, – это прошлый опыт ученика в решении задач, аналогия, ассоциации, которые может вызвать решаемая задача.

Достоинством синтетического метода является компактность, достигаемая при изложении готовых решений, полученных в процессе синтетического или аналитического поиска.

Несмотря на низкую поисковую и дидактическую эффективность синтетического метода, он пользуется популярностью у школьников и даже учителей, поскольку весьма прост и не требует большого мыслительного напряжения.