Метод наименьших квадратов.

 

Для оценки параметров а и b используется метод наименьших квадратов (МНК), по которому минимизируется сумма квадратов отклонений эмпирических значений от теоретических значений, т.е. найденных по уравнению регрессии:

Находя частные производные по а и b, приравнивая их к нулю, получаем систему уравнений, которую называют системой нормальных уравнений метода наименьших квадратов для прямой:

Решая эту систему определяем значения переменных a и b.

Однако, определить параметры линейного уравнения регрессии можно другим способом:

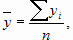
Если разделить первое уравнение на n, то получим , где отсюда получаем: .

Подставив это выражение во второе уравнение системы, получим формулу для определения параметра b уравнения регрессии.

где , .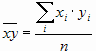

Коэффициент регрессии b показывает на сколько единиц в среднем изменяется переменная у при изменении переменной х на одну единицу.

Постоянная a дает значение зависимой переменной при нулевом значении х.

Возвращаясь к примеру зависимости прибыли предприятия от выработки продукции, обработаем статистические данные с помощью компьютерное программы «EconometricViews». Результаты представлены в следующей таблице:

 

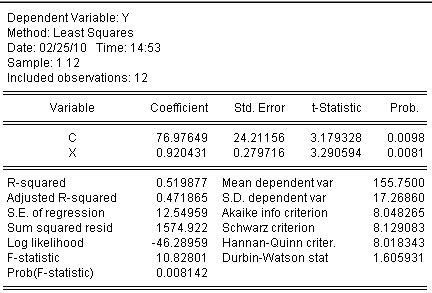
Таким образом, уравнение парной линейной регрессии зависимости прибыли предприятия от выработки продукции на одного человека имеет вид

у=76,98+0,92х.

На основании коэффициента регрессии перед переменной х, можно заключить следующие, если выработка продукции увеличится на 1 единицу на человека, можно ожидать увеличение прибыли предприятия на 0,92 тыс. тг.