Правила суммы и произведения
Лекция 3. КОМБИНАТОРИКА
Комбинаторика представляет собой область математики, занимающейся подсчётом элементов конечных множеств. Общие задачи подсчета элементов некоторого множества связаны с выборкой некоторого числа элементов из заданного базисного множества. Такие задачи полезно делить на типы в зависимости от того, как выбираются элементы: с повторением или без повторений, с учетом порядка выбора или без оного. Мы выведем формулы для каждого из перечисленных типов задач
Начнем с формулировки ряда простых задач.
Задача 1. В небольшой кондитерской к концу рабочего дня осталось несколько пирожных: четыре ванильных, два шоколадных и три фруктовых. Один покупатель собирается купить пирожные перед закрытием кондитерской. Сколько вариантов выбора существует, если покупатель может купить 1, 2, 3 пирожных?
Первая задача решается простым подсчетом. Поскольку все пирожные различны, мы просто можем сложить их количества. Это дает 4 + 2 + 3 = 9 пирожных, из которых покупатель может сделать выбор. Во втором случае 9*8=72 варианта выбора пирожных, в третьем 9*8*7= 504, если не важно какие именно пирожные выбирать!
Эти задачи иллюстрируют два фундаментальных правила пересчета.
Правило суммы гласит, что если А и В — несвязанные события, и существует n1 возможных исходов события A, и n2 возможных исходов события B, то возможное число исходов события «А или B» равно сумме n1 + n2 .
Правило произведения утверждает, что если дана последовательность к событий с n1 возможными исходами первого, n2 - второго, и т. д., вплоть до nk возможных исходов последнего, то общее число исходов последовательности k событий равно произведению n1 * n2*…* nk.
Задача 2. Сколько существует трехзначных чисел, начинающихся с 3 или 4? Трехзначные числа, о которых идет речь в задаче, разбиваются на два непересекающихся класса. К одному из них относятся числа, начинающиеся с 3, а ко второму - с 4. Для подсчета чисел в первом классе заметим, что существует один возможный исход для первой цифры (она должна быть равна 3), 10 исходов для второй и 10 исходов для последней цифры.
По правилу произведения получаем, что всего чисел в первом классе насчитывается ровно 1*10*10 = 100. Аналогично можно подсчитать количество чисел во втором классе. Оно тоже равно 100. Наконец, по правилу суммы получаем, что существует 100 + 100 = 200 трехзначных чисел, начинающихся с 3 или 4.
Задача 3. Государственный регистрационный знак легкового автомобиля состоит из трех цифр и трех букв русского алфавита (не считая кода города). Будем считать, что в номере можно задействовать любую последовательность букв и цифр. Сколько различных автомобильных номеров может выдать ГИБДД?
Решение. Каждую из трех букв номера можно выбрать из 33 букв алфавита. По правилу произведения число различных последовательностей из трех букв равно 33*33*33 = 35937. Аналогично, число последовательностей трех цифр равно 10*10*10 = 1000. Наконец, поскольку каждый из автомобильных номеров состоит из трех букв и трех цифр, правило произведения дает искомый ответ: 35937000 различных автомобильных номеров может выдать ГИБДД.
Задача 4. Ребенку предложили мешок с конфетами трех наименований: «Мишка на севере» (А), «Карамель» (В) и «Шоколад» (С). Сколькими способами ребенок может выбрать две конфеты из мешка?
На этот вопрос можно дать несколько ответов в зависимости от уточнения его формулировки. Ставя задачу, мы не уточнили, можно ли брать конфеты одного наименования или нет. Например, можно ли взять две конфеты «Мишка на севере», т.е. АА. Кроме того, имеет ли значение порядок выбора? Иными словами, отличается ли выбор АВ от ВА или нет?
Таким образом, мы имеем четыре разных уточнения формулировки.
1. Повторения разрешены и порядок выбора существенен. В этом случае у нас есть 9 возможностей: АА, АВ, АС, АВ, ВВ, ВС, С А, С В и СС.
2. Запрещено брать конфеты одного наименования, но порядок существенен. В этой ситуации - 6 случаев: АВ, АС, В А, ВС, С А и СВ.
3. Повторения разрешены, но порядок выбора не имеет значения. Тогда ответ - тоже 6 возможностей: АА, АВ, АС, ВВ, ВС и СС.
4. И, наконец, если нельзя брать одинаковые конфеты, а порядок не имеет значения, то у ребенка есть только три варианта выбора: АВ, АС и ВС.
Чтобы различать на терминологическом уровне тип конкретной задачи, введем несколько определений.
Начнем со вспомогательных терминов. Предположим, что мы берем элементы x1, x1, ..., xk из множества X мощности k ( число элементов в множестве равно k). Каждый такой набор принято называть выборкой объема k из n элементов или, иначе, (n, k)-выборкой. Выборка называется упорядоченной, если порядок следования элементов в ней задан. При этом две упорядоченные выборки, различающиеся лишь порядком следования элементов, считаются разными. Если же порядок следования элементов в выборке не имеет значения, то выборка называется неупорядоченной.
Теперь введем основные термины в соответствии с типом уточнений, приведенных выше.
• (n, k)-размещением с повторениями называется упорядоченная (n, k)-выборка, элементы в которой могут повторяться;
• (n, k)-размещением без повторений называется упорядоченная (n, k)-выборка, элементам в которой повторяться запрещено;
• неупорядоченная (n, k)-выборка с повторяющимися элементами называется (n, k)-сочетанием с повторениями
• неупорядоченная (n, k)-выборка без повторяющихся элементов называется (n, k)-сочетанием без повторений.
Подсчитаем количество всех различных (n, k)-размещений с повторениями. На первое место выборки мы можем поставить любой из n элементов множества. Поскольку повторения разрешены, то на второе место мы опять можем поставить любой элемент из этого же множества, и т. д. Поскольку у нас k мест в выборке, то опираясь на правило произведения, получаем, что число всех (n, k)-размещений с повторениями равно nk.
Задача 5. Целые числа в компьютере представляются строчкой из N двоичных знаков. Первый из них отведен на знак (+ или -), а остальные N - 1 отвечают за модуль целого числа. Сколько различных целых чисел может использовать компьютер?
Решение. Двоичная цифра это 0 или 1. Для записи числа используется N таких цифр. Заметим, что двоичные строки, представляющие числа, могут иметь повторяющиеся цифры, и порядок их следования, естественно, существенен для данной задачи. Поэтому мы имеем дело с (2, N)-размещениями с повторениями. По выведенной формуле получаем, что общее количество таких строк равно 2N.
Практически всегда различные размещения изображают различные числа, за исключением двух строк: -000000…00 и + 000000…00, которые изображают 0. Значит, компьютер может оперировать (2N - 1) целыми числами.
Для числа всех (n, k)-размещений без повторений зафиксировано специальное обозначение P(n, k).Подсчитаем это число. На первое место выборки мы можем поставить любой из n элементов. Поскольку здесь нам не разрешены повторения, то для второго места мы можем выбрать любой из (n- 1) оставшихся элементов. На третье - из (n- 2) и так далее, вплоть до k-го места, куда можно написать любой из (n-k +1) элементов. Теперь применим правило произведения. Имеем Р(n, k) = n(n-1)(n - 2) … (n-k +1).
Для сокращения записи напомним, что произведение всех натуральных чисел от 1 до n включительно называется n факториал и обозначается символом n!. Выразим Р(n, k)
 число различных (n, k)- размещений без повторений.
число различных (n, k)- размещений без повторений.
Число всех (n, k)- сочетаний без повторений обозначается символом С(n, k). Оно связано с числом (n, k)- размещений без повторений Р(n, k) формулой 
Задача 6. По меню в ресторане можно выбрать ровно три из семи главных блюд. Сколькими способами Вы можете сделать заказ?
Решение. Здесь мы имеем дело с (7, 3)-сочетаниями без повторений.
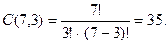 Итак, у Вас есть 35 возможностей для различных заказов.
Итак, у Вас есть 35 возможностей для различных заказов.
Исследуем, это сочетания с повторениями. Напомним, что это выборки, в которых порядок не важен, а вот повторы элементов допускаются. Поскольку порядок в наших выборках значения не имеет, а повторы разрешены, мы можем сгруппировать вместе одинаковые элементы, разделив группы какими-нибудь метками.
Предположим, например, что мы сделали выборку, состоявшую из пяти букв, каждая из которых может быть одной из а, 6^ и е.
Выборку, состоящую из двух «а», одной «б» и двух «в», можно записать как аа|б|вв, а выборка из одной буквы «а» и четырех букв «в» будет выглядеть так: а||вввв. Договоримся, что слева от первой метки либо стоят буквы «а», либо ничего, справа от второй метки - либо «в», либо ничего, а буквы «б», если они присутствуют в выборке, стоят между метками. Таким образом, можно считать, что мы всегда смотрим на семь ячеек (пять букв и две метки), причем различные выборки будут отличаться ячейками, в которых стоят метки. Значит, число всех таких сочетаний с повторениями совпадает с количеством способов, которыми мы можем поместить две метки в семь ячеек. Осталось понять, что это количество есть не что иное, как число всех (7, 2)- сочетаний без повторений, т. е. равно С(7, 2). Действительно, первую метку можно поставить в любую из семи ячеек, а вторую - в любую из шести, поскольку одна ячейка уже занята. Это дает нам 7 * 6 возможностей. Поменяв расставленные метки местами, мы получим то же самое заполнение ячеек. Стало быть, 7*6 нужно разделить на 2. Итак, количество способов равно
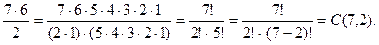
Возвращаясь к общему случаю (n, k)-сочетаний без повторений (k объектов из n данных), заметим, что нам потребуется n-1 метка и k объектов. Таким образом, у нас будет (n- 1) + k ячеек для заполнения. Значит, число (n, k)-сочетаний без повторений совпадает с количеством способов размещения (n- 1) метки в (n+k-1) ячейку. Итак, общее число (n, k)-сочетаний без повторений равно 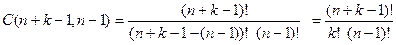
В таблице запишем все формулы для подсчета количества выборок k элементов из n-элементного множества, которые мы вывели сегодня.
