Термодинамические потенциалы. Энергия Гиббса. Энергия Гельмгольца
В изолированных системах энтропия только увеличивается и при равновесии достигает максимума. Поэтому она может быть использована в качестве критерия возможности протекания самопроизвольных процессов в таких системах. Однако на практике большинство процессов происходит в неизолированых системах, вследствие чего для них надо выбрать свои критерии направления самопроизвольных процессов и достижения равновесия. Такие критерии выражаются иными термодинамическими функциями, отличными от энтропии. Они называются характеристическими функциями.
Рассмотрим объединенный первый и второй закон термодинамики в дифференциальной форме:
TdS ³ dU + dA' + pdV, (36).
Выразим отсюда элементарную полезную работу dA':
dA' £ -dU + TdS - pdV, (37)
Рассмотрим два случая:
1) Пусть система переходит обратимо из состояния 1 в состояние 2 при V = const, Т = const, т.е. рассмотрим обратимый изохорно-изотермический процесс. Получим (т.к. dV = 0):
dА'= -dU +TdS – pdV = - dU+d(TdS) = -d(U –TS). (38)
Под знаком дифференциала стоит некоторая функция состояния. Обозначим ее через F:
U – TS º F (39)
и назовем энергией Гельмгольца (старое название: изохорно-изотермический потенциал). Тогда получим:
dА' = – dFV,T. (40)
Если проинтегрировать (40), то получим:
А' = – DFV,T (41)
величина DF = F2 – F1 – изменение энергии Гельмгольца, а
–DF = F1 – F2 – убыль энергии Гельмгольца.
Энергия Гельмгольца является одним из так называемых термодинамических потенциалов.
Термодинамический потенциал – это такая функция состояния системы, убыль которой при обратимом переходе из состояния 1 в состояние 2 при двух постоянных параметрах (x и y) равна максимальной полезной работе обратимого процесса А'= -∆Пх,у
2) Рассмотрим обратимый изобарно-изотермический процесс (р = cosnt, Т = cosnt) и проанализируем соотношение (38):
dА' = – dU +TdS – pdV = – dU +d(TS) – d(рV) = – d (U – TS + pV) = – d(H – TS).
Под знаком дифференциала стоит другая функция состояния. Обозначим ее через G:
Н – TS º G(42)
и назовем энергией Гиббса (старое название: изобарно-изотермический потенциал). Тогда получим:
dА' = – dGр, Т (43)
Проинтегрировав (43) получаем:
А' = – DGр, Т (44)
Здесь DG = G2 – G1 – изменение энергии Гиббса, – DG=G1 – G2 – убыль энергии Гиббса.
В ходе обратимого перехода системы из состояния 1 в состояние 2 при постоянных давлении и температуре совершаемая системой полезная работа равна убыли энергии Гиббса (– DG).
Для необратимых процессов, т.к. А'необр<А'обр, можно записать
А'необр< -∆FV,T и А'необр< -∆Gp,T
Используя соотношение (38), можно показать, что при определенных условиях термодинамическими потенциалами, кроме G, F, являются также внутренняя энергия U (изохорно-изоэнтропийный потенциал) и энтальпия Н (изобарно-изоэнтропийный потенциал),
Изменения термодинамических потенциалов можно рассматривать как критерии возможности протекания самопроизвольных процессов и равновесия в термодинамических системах.
В ходе самопроизвольного процесса, протекающего в соответствующих условиях, система сама совершает работу (А'>0) тогда при V,T=const, для необратимого самопроизвольного процесса
-∆F>0; ∆F<0; F2-F1<0; F2<F1
а при p,V=const DG>0, DG<0, G1-G2<0, G2-G1
при равновесии DFV,T = 0, DGр,Т = 0.
Термодинамические потенциалы в ходе самопроизвольного процесса уменьшаются и достигают минимума при равновесии.
Если нарисовать как и для энтропии графики изменения термодинамического потенциала П в зависимости от пути процесса, то экстремальной точкой, соответствующей равновесию, будет минимум (в отличие от энтропии):
 |
АВ – необратимый самопроизвольный процесс (здесь DПх,у < 0);
ВA – необратимый несамопроизвольный процесс (здесь DПх,у > 0);
точка В – соответствует равновесному состоянию (здесь DПх,у = 0).
2.5 Характеристические функции. Уравнения Гиббса–Гельмгольца.
Характеристическими функциями называются такие функции состояния системы, посредством которых и их частных производных могут быть выражены в явной форме все термодинамические свойства системы.
Из дифференциальной формы объединенного первого и второго законов термодинамики для обратимых процессов выразим величину dU:
TdS = dU + dA' + pdV, откуда
dU = TdS – dA' – pdV. (45)
Если полезная работа отсутствует (т.е. dA' = 0), то получим:
dU = TdS – pdV (46)
Вспомним теперь следующие соотношения:
G º H – TS = U + pV – TS (47)
F º U – TS (48)
Если найти значения полных дифференциалов dG, dF из соотношений (43)-(44) и учесть соотношение (46) для dU, то можно получить следующие выражения для dG, dF:
dG = dU + pdV + Vdp - TdS -SdT =Vdp – SdT (49)
dF = dU - TdS - SdT = – pdV – SdT (50)
На основании соотношений (49)–(50) можно прийти к выводам, что
G = G(р, Т); F = F(V, Т),
тогда, записав значения соответствующих полных дифференциалов для dG, dF через соответствующие частные производные, например,

 ,
,
и сравнив их с выражениями (49)–(50), можно получить следующие выражения для определения термодинамических свойств:
 (51);
(51);  (53);
(53);
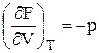 (52);
(52); 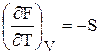 (54).
(54).
Таким образом, мы показали, что G, F являются характеристическими функциями.
C помощью полученных выше соотношений можно получить выражения, называемые уравнением (или уравнениями) Гиббса-Гельмгольца. Из уравнений (47) и (48) легко получить следующие выражения, учитывая, что температура – постоянная:
DG = DH – TDS (55)
DF = DU – TDS (56)
Так как,  , то (57)
, то (57)
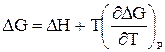 , (58)
, (58)
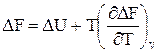 . (59)
. (59)
Последние два равенства и есть искомые зависимости  и
и  от температуры и их называют уравнениями Гиббса-Гельмгольца.
от температуры и их называют уравнениями Гиббса-Гельмгольца.