Второй закон термодинамики.
Второй закон термодинамики. Энтропия. Вычисление изменения энтропии для различных процессов. Постулат Планка. Энергия Гиббса и энергия Гельмгольца. Уравнение Гиббса-Гельмгольца. Самопроизвольное протекание химических реакций. Расчет изменения энергии Гиббса в химических реакциях. Химический потенциал. Активность и летучесть.
Первый закон термодинамики не дает критериев направления самопроизвольных и несамопроизвольных процессов и условий, при которых наступает состояние равновесия. Лишь с появлением в термодинамике понятия энтропия появляется строгий критерий направления самопроизвольных процессов. Термин энтропия, как и второй закон термодинамики, были введены Клаузиусом в середине ХIХ века. Карно показал, что в тепловых машинахтеплота, полученная от источника тепла, не может быть полностью переведена в механическую работу, а часть ее должна быть передана третьему телу – холодильнику. Это обобщение по существу выражает второй закон термодинамики и может рассматриваться как одна из формулировок второго закона термодинамики. Рассмотрим также некоторые другие формулировки второго закона:
Формулировка Клаузиуса (1850 г.). Не возможен самопроизвольный процесс передачи теплоты от холодного тела к горячему.
Формулировка Кельвина (Томсона) (1851 г.). Не возможно превратить теплоту какого-либо тела в работу, не производя никакого другого действия, кроме охлаждения этого тела;
Формулировка по Оствальду. Вечный двигатель второго рода невозможен (т.е. не существует машины, которая бы полностью превращала теплоту в работу).
Клаузиус, рассматривая обратимый циклический процесс, состоящий из двух изотерм и двух адиабат (см. учебники), разбил его на бесконечно малые участки, просуммировал (учитывая знаки dQ) все величины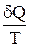 
(элементарная приведенная теплота), и показал, что для обратимого процесса
.
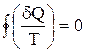Если вспомнить свойства функции состояния, то для какой-то функции состояния Z интеграл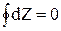 
, поэтому величина 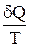связана с какой-то функцией состояния. Эту функцию состояния назвали энтропией (S).
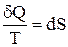или 
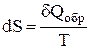, (1)
Выражение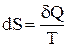 
(равенство Клаузиуса) – это дифференциальная форма записи второго закона термодинамики для обратимых процессов. Для необратимых процессов, как показал Клаузиус, справедливо неравенство
dS >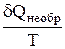
, (2)
это дифференциальная форма записи второго закона термодинамики для необратимых процессов. В общем виде дифференциальная форма записи второго закона термодинамики для обратимых и необратимых процессов может быть представлена в виде:
dS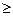 
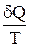, (3)
Единица измерения энтропии - такая же как и у соответствующей теплоемкости: молярной (мольной) –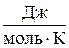 
, удельной –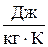 
.
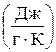Энтропия – экстенсивная величина, т.е. пропорциональна массе системы.
Из дифференциальной формы записи второго закона термодинамики легко можно получить интегральную форму записи этого закона:
; 
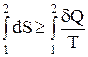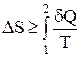(4)
Первый и второй законы термодинамики можно объединить в так называемый объединенный первый и второй закон термодинамики, который для обратимых процессов можно записать следующим образом:
ТdS = dU + dA¢ + pdV. (5)
Если работа производится системой только против внешнего давления, то dA¢ = 0 и получаем:
ТdS = dU + pdV (6)
Отсюда вытекает, что:
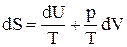, (7)
т.е. энтропия S является функцией внутренней энергии U и объема V: S = f(U,V).
В общем виде объединенный первый и второй закон термодинамики можно записать следующим образом:
ТdS 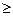dU + dA¢ + pdV (8)
Если рассматривать только объемную работу, то получим:
TdS 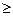dU + pdV (9)
Второй закон термодинамики для изолированных систем.
Для изолированной системы dQ = 0, m = const, U = const, V = const. Для необратимых процессов, протекающих в такой системе, можно записать, что
dSнеобр. > 0
DSнеобр. > 0 т.е. S2 > S1 (11)
Выражения dS > 0 и DS > 0 можно рассматривать как математическую запись второго закона термодинамики, который для изолированной системы формулируется следующим образом:
в изолированной системе любой самопроизвольный процесс протекает только с увеличением энтропии, причем процесс закончится тогда, когда энтропия S достигнет своего максимального значения (когда наступит состояние равновесия).
При равновесии S2 = Smax = const и DS = 0. Схематически все сказанное можно изобразить на графике зависимости S от пути процесса:
 |
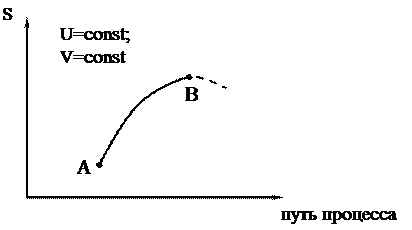Путь процесса – это какая-либо величина, которая меняется при протекании процесса и поддается опытному определению.
Участок АВ – необратимый самопроизвольный процесс (DS > 0), энтропия возрастает; участок ВA – необратимый нeсамопроизвольный процесс (DS < 0), энтропия уменьшается; точка В – равновесное состояние (S=Smax).
Следует отметить, что если процесс протекает в неизолированной системе, то для оценки необратимости процесса необходимо иметь величину изменения энтропии системы и величину изменения энтропии окружающей среды.