Графическое изображение статистических рядов.

Для наглядности строят различные графики статистического распределения, и, в частности, полигон и гистограмму.

Полигоном частот (относительных частот) называют ломаную, отрезки которой соединяют точки , , …, (,, …, ). Для построения полигона частот (относительных частот) на оси абсцисс откладывают варианты , а на оси ординат – соответствующие им частоты 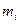(относительные частоты ). Точки (или ) соединяют отрезками прямых и получают полигон частот (относительных частот).

Изобразим полигон относительных частот следующего распределения:

	1,5	3,5	5,5	7,5
	0,1	0,2	0,4	0,3

Полигон применяется для изображения как дискретных, так и интервальных статистических рядов. Для изображения интервальных рядов применяется также гистограмма.

Гистограммой частот (относительных частот) называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною , а высоты равны отношению (соответственно ), где – плотность частоты (– плотность относительной частоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии .

Пример 25.2. Построить гистограмму частот по данному распределению выборки.

 

Частичный интервал длиною	Сумма частот вариант частичного интервала	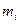Плотность частоты
5–10	4	0,8
10–15	6	1,2
15–20	16	3,2
20–25	36	7,2
25– 30	24	4,8
30–35	10	2,0
35–40	4	0,8

Решение. Гистограмма частот имеет следующий вид:

Отметим, что если на гистограмме частот соединить середины верхних сторон элементарных прямоугольников, то полученная замкнутая ломаная образует полигон распределения частот.

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии .