Гидродинамика несжимаемой жидкости .Уравнение Бернулли. Формула Торричелли.

Лагранжев и Эйлеров способ описания движения. Поле векторов скорости, линии тока. Густота линий тока.

рис. 2. Линии тока

 

Если вектор скорости в каждой точке пространства остается по­стоянным, то течение называется установившимся, или стационарным. При стационарном течении любая частица жидкости проходит данную точку пространства с одним и тем же значением v. Картина линий тока при стационарном течении остается неизменной, и линии тока в этом случае совпадают с траекториями частиц.

Часть жидкости, ограниченная линиями тока, назы­вается трубкой тока. Вектор v, будучи в каждой точке касательным к линии тока, будет касательным к поверхности трубки тока; следовательно, частицы жидкости при своем движении не пересекают стенок трубки тока.

рис. 3. Трубки тока

Возьмем трубку тока, настолько тонкую, что в каждом ее сечении скорость можно считать постоянной. Если жидкость несжимаема (т. о. плотность ее всюду одинакова и изменяться не может), то количество жидкости между сечениями S₁ и S₂ (рис. 3) будет оставаться неизменным. Отсюда следует, что объемы жидкости, протекающие за еди­ницу времени через сечения S₁ и S₂, должны быть оди­наковы:

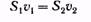
Приведенное выше рассуждение применимо к любой паре сечений S₁и S₂. Следовательно, для несжимаемой жидкости величина Sv в любом сечении одной и той же трубки тока должна быть одинакова:

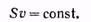(16.8)

Выражение (16.8) представляет собой содер­жание теоремы о неразрывности струи.

Рассматривая движение жидкостей, во многих слу­чаях можно считать, что перемещение одних частей жидкости относительно других не связано с возникновением сил трения. Жидкость, в которой внутреннее трение (вязкость) полностью отсутствует, называется идеальной.

рис.4

Возьмем сечение трубки тока и отрезки DV₁ и DV₂ настоль­ко малыми, чтобы всем точкам каждого из заштрихо­ванных объемов можно было приписать одно и то же значение скорости v, давления р и высоты h.

Тогда приращение энергии запишется следующим образом:

(16.9)

В идеальной жидкости силы трения отсутствуют. По­этому приращение энергии (16.9) должно равняться работе, совершаемой над выделенным объемом силами давления. Отлична от нуля лишь работа сил, приложенных к сечениям S₁ и S₂. Эта работа равна

(16.10)

Приравнивая выражения (16.9) и (16.10), сокращая на DV и перенося члены с одинаковыми индексами в одну часть равенства, получим:

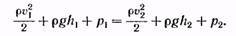(16.11)

Полученный нами результат можно сформулировать следующим образом: в стационарно текущей идеальной жидкости вдоль любой линии тока выполняется условие

(16.12)

Уравнение (16.11) или равнозначное ему уравнение (16.12) называется уравнением Бернулли. Не­смотря на то, что это уравнение было получено для идеальной жидкости, оно достаточно хорошо выпол­няется для реальных жидкостей, внутреннее трение в которых не очень велико.

Рассмотрим некоторые следствия, вытекающие изуравнения Бернулли. Пусть жидкость течет так, что скорость имеет во всех точках одинаковую величину. Тогда согласно (16.12) для двух произвольных точек лю­бой линии тока будет выполняться равенство

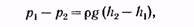(16.13)

откуда следует, что распределение давления в этомслучае будет таким же, как в покоящейся жидкости

Для горизонтальной линии тока условие (16.12) при­нимает вид

(16.14)

т. е. давление оказывается меньшим в тех точках, где скорость больше (качественно это уже было показано в предыдущем параграфе).