Лингвистический автомат.

Минимизация числа состояний автомата

Алгоритм на основании языка L, порождаемого автоматом.

Идея: разбить множество состояний на непересекающиеся множества неразличимых состояний.

Строятся матрицы D₀, D₁,… указывающие различимость состояний по строкам длины n. Состояния q_i и q_j различимы по строке длины 0( 1 на пересечении строки i и столбца j матрицы D₀): q_i D₀ q_j Û (q_iÎK ) & ( q_jÏ K) Ú (q_iÏ K)&( q_jÎK).

Далее определение по индукции: при i > 0 состояния q_k и q_j различимы по строке длины i, т.е. (q_k D_i q_j )Û q_k D_i-1 q_j или $aÎV_T , такой, что F(q_k,a) D_i-1 F(q_j,a).

Состояние q_k различимо от состояния q_j , если $ i³ 0 , такое, что q_k D_i q_j .

Очевидно, что q_k D_i q_j Û существует строка Х, ½Х½£ i , что (F(q_i, X)ÎK ) & ( F(q_j, X)Ï K) Ú (F(q_i, X)Ï K)&( F(q_j, , X)ÎK).

Пример.

Диаграмма автомата представлена на рис. 16.

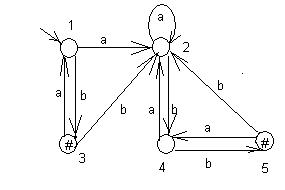
Рис.16

Матрицы, получающиеся при анализе автомата:

 

 

D0

F T F T T F T T F T

D1

F T F T T T T T F T

D1=D2

 

Из анализа полученной матрицы получаем три класса эквивалентных состояний:

K₁ = {1, 4}, K₂ = {2}, K₃ = {3,5}. Диаграмма полученного автомата представлена на рис. 17.

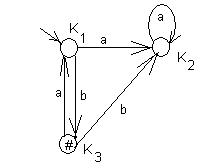
Рис.17