Детерминизация конечных автоматов

Для того, чтобы построить соответствующее таким грамматикам автоматы, можно рассматривать переходы F автомата Q ´ V_T в множество подмножеств Q ( т.е. в P(Q)). При этом

½P(Q)½=2^½Q½.

Будем называть недетерминированным конечным автоматом S пятерку объектов S =<Q, V_T, q₀, F, K>, где интерпретация Q, V_T, q₀, K такая же, как и раньше, а F – отображение Q ´ V_T в P(Q).

Определение цепочек, допускаемых автоматом, остается прежним, но если в детерминированном автомате последовательность конфигураций однозначно определялась заданием входной цепочки, так как из каждой конфигурации автомат мог перейти не более чем в одну конфигурацию, то в недетерминированном случае это не так. Поэтому при интерпретации определения "цепочка X допущена" как (q₀,x) ├ (q,l)&qÎKнеобходимо при анализе цепочки, моделируя работу автомата, перебрать варианты выполнения тактов, чтобы найти тот (или те), которые приводят в заключительную ситуацию. В силу тех же соображений (тождественность движений по графу и при порождении цепочки, и при ее допускании) можем утверждать, что для любой грамматики G может быть построен конечный автомат A (в общем случае недетерминированный), такой, что L(G)=L(A) . Соответствия между параметрами грамматики и автомата остаются те же.

Возникает естественный вопрос о соотношении класса языков, допускаемых детерминированными и недетерминированными автоматами. Ясно, что для любого детерминированного автомата A существует недетерминированный A' допускающий тот же самый язык (достаточно в качестве A'взять А). Но верно ли обратное? Ответ на этот вопрос дает следующая теорема.

Теорема 1. ЕслиL=L(A) для некоторого недетерминированного автомата A , то найдется конечный автоматA'такой, чтоL(A')=L(A).

Доказательство:

Пусть дан недетерминированный конечный автомат А =<Q, V_T, q₀, F, K>. Построим соответствующий детерминированный автомат А’=<Q’, V_T, q₀’, F’, K’>

Q’ = P(Q) . При этом множество состояний 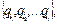будем обозначать как .

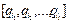q₀’=[q₀].

K’ = {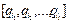/ 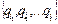ÇK ¹Æ}

F’(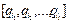, a)=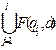

Несложно доказать методом математической индукции, что для любого I

([q₀],XY) ├ⁱ_A’(B,Y) Û B={p/ (q₀, XY) ├ⁱ_A(p,Y)}

½X½=i.

Значит, для любой цепочки Х

([q₀],X) ├ⁱ_A’(B,l) Û B={p/ (q₀, X) ├ⁱ_A(p,l)}

Поэтому, в случае BÎ K’, т.е. если Х – цепочка, допускаемая детерминированным автоматом, то в исходном недетерминированном автомате существует путь из начального в конечное состояние при чтении этой цепочки, и, следовательно, L(A)=L(A’).

Т.о., сопоставляя доказанные утверждения, получаем:

Класс А-языков и класс языков, распознаваемых конечными автоматами, совпадает.

Так, например, для автомата, представленного на рис. 5, соответствующий детерминированный автомат представлен на рис. 6.

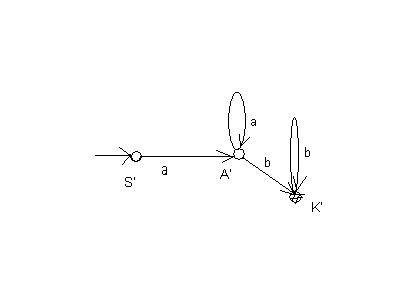
Рис.6

 

Здесь F(S,a)= [S,A] = A’

F([S,A], a) = [S,A]

F([S,A],b) = [A, K] = K’

F([A,K],b)= [A, K] = K’

Для автомата на рис. 7а детерминированный автомат представлен на рис.7b.

 

 

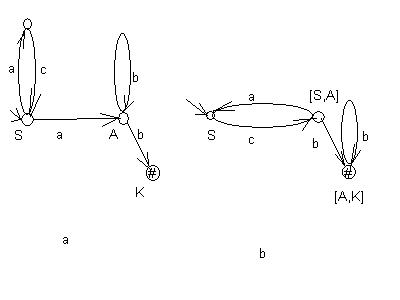
Рис.7

Алгоритм построения детерминированного автомата по недетерминированному:

Строим начальное состояние q₀’= [q₀], помечаем его как начальное.

Для каждого состояния, построенного на предыдущем шаге, строим

F(q_i’, a) для всех aÎV_T. Если для какого-нибудь из построенных состояний функция перехода ещё не построена, возвращаемся к шагу 2.

Помечаем как конечные все состояния q_i’=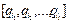/ 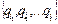Ç K¹Æ.

Конечность процесса обеспечивается конечностью множества P(Q).